About

For Teachers

- CM_SHM.wmv
- CM_SHM.mp4
- .DS_Store
- .DS_Store

Credits

Author: video jit ning, model lookang

Document Brief: Simple Harmonic Motion (SHM) and Circular Motion Tracker Analysis

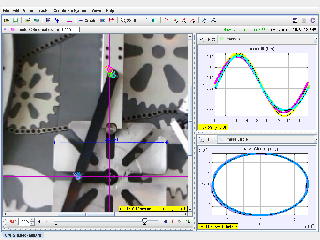
This document presents an analysis of simple harmonic motion (SHM) and circular motion, as visualized through the movement of a mass and gears in a system. Using Tracker software, the relationship between SHM, circular motion, and oscillatory motion is explored through graphical and video-based analysis.

Purpose:

To demonstrate the connection between SHM and circular motion and analyze the parameters of oscillation using real-time tracking and graphing.

Key Features:

• Motion tracking of a system involving gears and a pendulum.
• Analysis of displacement ($y$) vs. time and circular trajectories ($x,y$).
• Graphical representation of periodic motion and its connection to SHM.
• Insights into the phase relationship between SHM and circular motion.

Study Guide: Understanding SHM and Circular Motion

Learning Objectives:

1. Understand the relationship between SHM and uniform circular motion.
2. Analyze the displacement-time graph for SHM and its sinusoidal nature.
3. Explore the $x,y$ trajectory graph to link SHM to circular motion.

Step-by-Step Guide:

1. Setup and Calibration:

   • Import the motion video into Tracker software.
   • Define the coordinate system and set a reference scale for measurements.

2. Tracking Motion:

   • Identify key components of the motion, such as the pendulum or circular mass, and track their motion frame by frame.
   • Observe the different models (e.g., Model A Circular and Model C Kinematics) plotted on the video.

3. Graphical Analysis:

   • Analyze the $y$-displacement vs. time graph:
     • Observe its sinusoidal nature, characteristic of SHM.
     • Determine the period ($T$) and amplitude ($A$) of oscillation.
   • Examine the $x,y$ trajectory graph:
     • Note how the motion traces a circular path, emphasizing the link between SHM (projection on one axis) and circular motion.
   • Compare theoretical predictions of SHM with measured data.

4. Applications:

   • Use the phase relationship between SHM and circular motion to understand oscillatory systems, such as pendulums or mechanical gears.
   • Extend the analysis to real-world systems, like clocks or vibrating objects.

Tips for Success:

• Calibrate the coordinate system and ensure accurate scaling for reliable data.
• Cross-check phase relationships by comparing different tracked points.

FAQ: SHM and Circular Motion Tracker

1. What is SHM, and how is it related to circular motion?

Simple harmonic motion (SHM) is oscillatory motion where the restoring force is proportional to displacement. SHM is the projection of uniform circular motion onto one axis.

2. Why does the $y$-displacement graph appear sinusoidal?

The sinusoidal shape arises because SHM is mathematically described by sine or cosine functions, reflecting the periodic nature of the motion.

3. What does the $x,y$ trajectory graph represent?

The trajectory graph shows the circular motion from which SHM is derived. The projection of this motion onto the $x$- or $y$-axis produces sinusoidal SHM.

4. How do we calculate the period and amplitude of SHM?

• The period ($T$) is the time for one complete oscillation, obtained from the $y$-displacement vs. time graph.
• The amplitude ($A$) is the maximum displacement from the equilibrium position.

5. Can this analysis be applied to other oscillatory systems?

Yes, the principles apply to pendulums, springs, and any system exhibiting SHM, such as molecular vibrations or electrical oscillations.

6. What are the practical applications of this model?

This analysis helps in understanding the behavior of oscillatory systems, designing mechanical clocks, studying waveforms, and analyzing engineering structures.