Translations

Code	Language		Translator	Run

Credits

Francisco Esquembre; Fu-Kwun Hwang; lookang; Felix J. Garcia Clemente; Shaun Quek

Authors/Creators: Francisco Esquembre, Fu-Kwun Hwang, lookang, Felix J. Garcia Clemente, Shaun Quek.

Overview:

These sources describe a simulation model designed to illustrate the spread of the COVID-19 virus within a population. The model, built using JavaScript and HTML5, allows users to interactively explore various factors influencing the pandemic, including the rate of spread, probability of infection, and the impact of interventions like work-from-home policies, lockdowns, and vaccination. The primary aim of this model appears to be educational, providing a visual and interactive way to understand the dynamics of infectious disease transmission and the effectiveness of different mitigation strategies.

Main Themes and Important Ideas/Facts:

1. Visual Representation of Virus Spread:

• The model visualizes a population of 100 individuals as "balls" moving randomly.
• The spread of the virus is represented by the "sick" balls infecting "healthy" balls upon close contact or "collision."
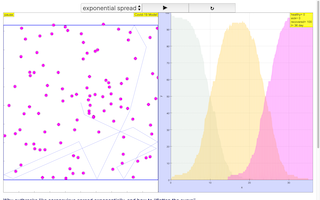
• A right panel displays graphs tracking the number of healthy, sick, and recovered individuals over time, providing a dynamic view of the outbreak's progression.
• Quote: "Left panel shows the visualization or the big picture view a population of 100 people, modelled as balls. Right panel show the graphs of healthy, sick and recovered people based on the colors representation."

2. Modeling Exponential Spread and "Flattening the Curve":

• The model demonstrates how a virus can spread exponentially due to random movement and probabilistic infection upon contact.
• It highlights the critical importance of slowing the spread ("flattening the curve") to prevent overwhelming hospital capacity.
• Quote: "Exponential spread is modelled using a random velocity and random direction, the spread of the virus from sick to healthy is probabilistic based on closeness or collision. The reason why each country is preventing this rapid growth rate to prevent filling up the hospitals to their maximum capacity, forcing emergency rooms to close their doors to new patients. This will likely lead to more deaths due to COVID-19."
• The model illustrates that a "slow spread," achieved through lower velocity and less frequent contact, results in a flattened sick curve, allowing healthcare systems to manage cases more effectively.

3. Impact of Social Distancing:

• Social distancing is modeled by introducing a "dotted circle" around each individual, representing a reduced probability of transmission unless individuals are within this close proximity for a sufficient time.
• The simulation suggests that effective social distancing can significantly reduce the spread and potentially "defeat" the virus by limiting transmission opportunities.
• Quote: "Social distancing is modelled using a dotted circle surrounding each ball where there is now a lower chance of the spread of the virus from sick to healthy as the virus probably need to be close enough and long enough time to transmit to the healthy. The simulation will run likely with little or low number of sick eventually and COVID-19 is defeated!"

4. Effectiveness of Work-From-Home and Lockdown Policies:

• "Half Work from home" is modeled by making half the population stationary after contact, reducing the chances of further spread.
• "All Work from home or also known as total lockdown" is modeled by making the entire population stationary, drastically limiting transmission opportunities.
• The model visually demonstrates how reducing movement and interaction within the population effectively curbs the virus's ability to spread.
• Quote (Half Work From Home): "Half Work from home is modelled using half of the total number of the balls stationary even after collision or contact, again there is now a lower chance of the spread of the virus from sick to healthy as the virus has a lower opportunity to transmit to the healthy"
• Quote (Total Lockdown): "All Work from home or also known as total lockdown, is modelled using all of the total number of the balls stationary even after collision or contact, again there is now a even lower chance of the spread of the virus from sick to healthy as the virus has a near impossible opportunity to transmit to the healthy"

5. Role of Vaccination:

• Vaccination is modeled by setting the probability of infection for vaccinated individuals to zero (p=0) even after contact with a sick individual.
• The simulation highlights that a high vaccination rate ("N=90" in the example) leads to a smaller pool of healthy individuals susceptible to the virus.
• Crucially, vaccination is shown to reduce the number of sick individuals, easing the burden on hospitals and potentially leading to fewer deaths due to better medical care.
• Quote: "Vaccinated, is modelled using if the person is vaccinated the probability of infection is reduced to zero, or p=0 even after collision or contact. In other words, the spread of the virus from sick to vaccinated persons is nearly impossible after vaccination."
• Quote: "The picture below shows how vaccinated causes the pool of healthy to be lower, but for vaccination to work against a virus, a large number needs to be vaccinated say N=90, where the sick will be a smaller number, easing the load on hospitals etc, so we may have a higher chance of lesser people dying after being sick due to good medical treatments and care in health care facilities."

6. Model Assumptions and Limitations:

• The model makes several simplifying assumptions that may not perfectly reflect real-world scenarios.
• Random Motion: People's movement is assumed to be completely random, which is unrealistic as many individuals follow regular patterns (work, school).
• Collision Physics: Healthy individuals move away from contact according to basic collision laws.
• Infection Dynamics: Sick individuals can only infect healthy individuals, and the first sick person remains sick until infecting another.
• Recovery Period: A fixed 14-day recovery period is assumed, which is arbitrary.
• No Reinfection: Recovered individuals are assumed to be immune, which may not always be the case.
• Social Distancing Effectiveness: Social distancing is modeled as completely preventing transmission within a certain distance, which might be inaccurate as the virus can spread through other means.
• Transmission Modes: The model primarily focuses on person-to-person spread through close contact and does not model spread from contaminated surfaces.
• Quote: "The motion of the people (balls) are completely random, this might not be the case in real life, most people travel to work or to school in a regular timing."
• Quote: "Social distancing completely makes the probability of virus spreading p = 0, which could be inaccurate as the virus could spread through 1. Person-to-person spread (modelled), 2.Spread from contact with contaminated surfaces or objects (not modelled)"

7. Interactive Features:

• Users can interact with the model by dragging "balls," particularly the initial "sick" ball, to control the initial outbreak size.
• The simulation offers dropdown menus for easy adjustment of various parameters, making it user-friendly.
• This interactivity allows for experimentation and observation of how different factors influence the pandemic's trajectory.
• Quote: "The simulation is designed to be simple to use via dropdown menu. the option are self explanatory."
• Quote: "Drag any balls, especially the sick ball to infect more balls at the beginning when time t = 0 day. This allows you to determine the initial number of sick."

8. Educational Purpose:

• The model is presented as an "Open Educational Resource" and aims to facilitate discussion and understanding of current affairs related to pandemic spread.
• The "Sample Learning Goals" explicitly mention "current affairs model based discussion with interactive."
• The "For Teachers" section provides context on exponential spread and "flattening the curve," suggesting its use in educational settings.

Conclusion:

The COVID-19 virus spread simulation model provides a valuable tool for understanding the fundamental principles governing infectious disease transmission. By visualizing the spread dynamics and allowing interactive manipulation of key parameters like transmission probability and intervention strategies, the model effectively illustrates the importance of public health measures such as social distancing, work-from-home policies, lockdowns, and vaccination in mitigating the impact of a pandemic. While acknowledging its simplifying assumptions, the model serves as a powerful educational resource for students, educators, and the general public seeking to grasp the complexities of viral outbreaks. The ongoing development and inclusion of "more options" indicate a commitment to enhancing the model's realism and educational value.

 

COVID-19 Virus Spread Model Study Guide

Quiz

1. According to the texts, what are the primary ways COVID-19 spreads from person to person?
2. The simulations model exponential spread based on what factors related to the movement and interaction of individuals?
3. How does the simulation represent the effect of "work from home" or total lockdown on virus transmission?
4. Explain how vaccination is modeled in the simulation and what the model suggests about the effectiveness of widespread vaccination.
5. What is meant by "flattening the curve" in the context of a disease outbreak, and how does the simulation illustrate this concept?
6. Describe one key assumption made in the COVID-19 spread model that might not accurately reflect real-world scenarios.
7. What does the simulation suggest about the relationship between the rate of virus spread and the capacity of hospitals to provide care?
8. How is social distancing modeled in the simulation, and what is the intended effect on the probability of virus transmission?
9. What role does the initial number of sick individuals play in the simulated spread of the virus, according to the "Interaction/Games" section?
10. Briefly describe the purpose of the graphs shown in the right panel of the simulation interface.

Answer Key

1. The primary ways COVID-19 spreads are through contact with an infected person when they cough or sneeze, and by touching a surface with the virus and then touching their eyes, nose, or mouth.
2. Exponential spread is modeled using a random velocity and random direction for the movement of individuals. The spread from sick to healthy individuals is probabilistic and based on their closeness or collision.
3. "Work from home" is modeled by making a portion (half or all) of the simulated individuals stationary after collision or contact, thus reducing the opportunity for the virus to transmit to healthy individuals.
4. Vaccination is modeled by reducing the probability of infection to zero (p=0) for vaccinated individuals, even after collision or contact with a sick person, indicating that the virus spread to vaccinated individuals is nearly impossible.
5. "Flattening the curve" refers to slowing the rapid increase in the number of sick individuals to prevent hospitals from being overwhelmed. The simulation shows that slower spread models result in a lower, flatter curve of sick individuals over time, allowing hospitals to manage the patient load.
6. One key assumption is that the motion of people (balls) is completely random, which might not be accurate in real life where many people travel to work or school with regular timing.
7. The simulation suggests that a rapid rate of virus spread can lead to hospitals filling up to their maximum capacity, potentially forcing emergency rooms to close and resulting in more deaths due to a lack of medical care.
8. Social distancing is modeled by a dotted circle around each individual. This reduces the chance of virus spread from sick to healthy individuals because transmission likely requires closer and longer contact.
9. The "Interaction/Games" section suggests that a larger initial number of sick individuals at the beginning of the simulation (time t=0) can lead to a more rapid spread of the virus within the population.
10. The graphs in the right panel visually represent the number of healthy, sick, and recovered individuals over time, based on the color representation in the left panel visualization.

Essay Format Questions

1. Discuss the strengths and limitations of using a simplified simulation model, like the one described, to understand the complex dynamics of a real-world pandemic such as COVID-19. Consider which factors are effectively modeled and which are oversimplified or omitted.
2. Analyze the various intervention strategies (work from home, lockdown, social distancing, vaccination) as they are modeled in the simulation. Evaluate their potential impact on controlling the spread of a virus based on the simulation's outcomes and discuss the real-world implications of these findings.
3. The simulation makes several explicit assumptions. Choose two of these assumptions and critically evaluate their validity in the context of the actual COVID-19 pandemic. How might the relaxation of these assumptions alter the simulation's results and its applicability to real-world scenarios?
4. The text highlights the goal of preventing hospitals from reaching maximum capacity. Explain how the simulation demonstrates the importance of controlling the virus spread in relation to healthcare system limitations and discuss the ethical considerations that arise when healthcare resources are strained during a pandemic.
5. Consider the "Sample Learning Goals" mentioned in the text ("current affairs model based discussion with interactive"). Describe how this simulation could be used as an educational tool to facilitate discussion and understanding of pandemic dynamics among students or the general public. What are the benefits and potential challenges of using such interactive models for learning about complex health issues?

Glossary of Key Terms

• Exponential Spread: A rapid increase in the number of cases where the growth rate is proportional to the current number of cases, leading to a steep upward curve.
• Probabilistic Spread: The transmission of the virus from a sick individual to a healthy one is not guaranteed upon contact but depends on a certain likelihood or probability, often influenced by factors like proximity and duration of interaction.
• Flattening the Curve: Reducing the steepness of the epidemic curve, which represents the number of new cases over time. This aims to prevent overwhelming healthcare systems by spreading out the total number of cases over a longer period.
• Social Distancing: Measures taken to reduce contact between people to slow down the transmission of a disease. In the simulation, this is represented by a reduced probability of infection within a certain radius.
• Work from Home/Lockdown: Policies that restrict movement and interaction by having people stay at home and reducing non-essential activities. In the model, this is shown by making individuals stationary, limiting transmission opportunities.
• Vaccination: The administration of a vaccine to provide immunity against a disease. The model represents vaccination as eliminating the probability of infection upon contact.
• Random Velocity and Direction: In the context of the simulation, the individuals (balls) move in unpredictable ways with varying speeds and angles, mimicking the random movements of people in a population.
• Collision Laws of Physics: Basic principles governing how objects interact when they come into contact, influencing their subsequent movement. This is used to model the movement of individuals after an interaction.
• Arbitrary Length of Days: A duration chosen for the simulation (e.g., the 14-day recovery period) that is not necessarily based on precise real-world data but serves as a parameter for the model.
• Visualization: The graphical representation of data or a process. In the simulation, the movement and status (healthy, sick, recovered) of the individuals are visually displayed.

Sample Learning Goals

current affairs model based discussion with interactive

For Teachers

Research

[text]

Video

[text]

 Version

 https://weelookang.blogspot.com/2020/04/covid-19-virus-spread-javascript-html5.html

Other Resources

[text]