Breadcrumbs

📊MAthematics PlaySpace Fractions Bar Model Interactive JavaScript Applet

 

 

 

 

Download ModelDownload SourceembedLaunch Website ES WebEJS

About

Intro Page Dev Notes. - Considering creating a key-value pair for each "related" arrow and box once the arrow has been snapped to the box. Currently, there can be multiple arrows to each box, causing them to overlap and not being able to assign arrows to different boxes. Things to work on: - Add label input boxes  

Translations

Code Language Translator Run

Credits

Mianna Teng; Loo Kang Wee; kyrin

Introduction:

This briefing document summarizes the key themes and information presented in two provided sources related to the use of the bar model method for teaching fractions in primary mathematics. The first source is an excerpt titled "Bar Model Method in Primary Math Only Fraction" by Mianna Teng, Loo Kang Wee, and kyrin. The second source is an excerpt from the "MAthematics PlaySpace Fractions Bar Model Interactive JavaScript Applet" page, which also credits Mianna Teng, Loo Kang Wee, and kyrin among others. These sources collectively highlight the importance, application, and available digital tools for implementing the bar model method in teaching fractions to primary school students.

2. Main Themes and Important Ideas:

2.1. The Bar Model Method as a Tool for Teaching Fractions:

Both sources clearly focus on the bar model method as a valuable pedagogical approach for introducing and developing understanding of fractions in primary mathematics. The title of the first excerpt, "Bar Model Method in Primary Math Only Fraction," emphasizes its specific application to fraction concepts. The second source details an interactive JavaScript applet specifically designed for visualizing and manipulating fractions using bar models.

2.2. Authorship and Collaboration:

The consistent crediting of Mianna Teng, Loo Kang Wee, and kyrin across both sources suggests their significant contribution to the development and promotion of this method and related resources. The "MAthematics PlaySpace" page also acknowledges other contributors like CH Thong and lists various resources, indicating a collaborative effort within the Open Educational Resources / Open Source Physics @ Singapore initiative.

2.3. Digital Tools and Interactivity:

The "MAthematics PlaySpace" excerpt heavily focuses on a specific interactive JavaScript applet for fractions using bar models. The inclusion of an embed code (<iframe width="100%" height="100%" src="https://iwant2study.org/lookangejss/math/ejss_model_MAPS_fractions10g/MAPS_fractions10g_Simulation.xhtml " frameborder="0"></iframe>) demonstrates the intention for educators to easily integrate this tool into their online teaching materials.

2.4. Features and Development of the Applet:

The "About" section of the applet page provides insights into its ongoing development. The developers mention considerations for creating "a key-value pair for each 'related' arrow and box once the arrow has been snapped to the box" to address the issue of overlapping arrows when multiple arrows are connected to a single box. The note "Things to work on: - Add label input boxes" indicates future enhancements aimed at improving the applet's usability and functionality. This highlights the iterative nature of educational resource development.

2.5. Accessibility and Open Educational Resources:

The context of "Open Educational Resources / Open Source Physics @ Singapore" suggests that the applet and likely the pedagogical ideas behind the bar model method are intended to be freely accessible and usable by educators. The license mentioned in the first source ("Released under a license") further supports this idea of open sharing.

2.6. Supporting Resources and Community:

The "Other Resources" section lists various external links to other bar model tools (e.g., "www.ace-learning.com/model-thinking-blocks-drawing-tool-free-version", "https://www.mathplayground.com/thinking_blocks_modeling_tool/index.html") and related blog posts by Loo Kang Wee ("https://weelookang.blogspot.com/2021/08/mathematics-playspace-fractions.html", "https://weelookang.blogspot.com/2021/12/mathematics-playspace-fractions-bar.html"). This indicates a broader community and a wealth of resources available for educators interested in using the bar model method. The inclusion of YouTube video links ("https://www.youtube.com/watch?v=S2vAHGD1_o4", "https://www.youtube.com/watch?v=UW8EJ0M3flc") suggests the use of multimedia to explain and demonstrate the method.

2.7. Breadcrumbs and Navigation:

The "Breadcrumbs" section ("Home > MAthematics PlaySpace Fractions Bar Model Interactive JavaScript Applet > Primary > Mathematics") provides context within a larger website structure, indicating that this applet is categorized under "Primary" and "Mathematics" within the "MAthematics PlaySpace."

2.8. Translations:

The presence of a "Translations" section with options for "Code," "Language," "Translator," and "Run" implies an effort to make the applet accessible to a wider audience through language localization, although no specific translations are listed in the excerpt.

2.9. Diverse Range of Educational Applets:

The extensive list of other applets available on the "Open Educational Resources / Open Source Physics @ Singapore" website (as seen in the accordion menu) showcases a broad commitment to developing interactive digital tools for various subjects and grade levels, with a significant focus on mathematics and science. While not directly about the bar model method, this context highlights the environment in which the fraction bar model applet was created.

3. Key Quotes:

  • From the embed section: <iframe width="100%" height="100%" src="https://iwant2study.org/lookangejss/math/ejss_model_MAPS_fractions10g/MAPS_fractions10g_Simulation.xhtml " frameborder="0"></iframe> - This provides the direct code for embedding the interactive bar model.
  • From the "About" section: "- Considering creating a key-value pair for each 'related' arrow and box once the arrow has been snapped to the box. Currently, there can be multiple arrows to each box, causing them to overlap and not being able to assign arrows to different boxes. Things to work on: - Add label input boxes" - This gives insight into the technical development and future plans for the applet.

4. Implications for Educators:

  • The bar model method is presented as a valuable visual strategy for teaching fractions in primary grades.
  • Interactive digital tools, such as the JavaScript applet highlighted, can enhance student engagement and understanding of fraction concepts through manipulation and visualization.
  • A community of educators and developers is actively contributing to and sharing resources related to the bar model method.
  • The open educational resource nature of these materials allows for free access and integration into teaching practices.

5. Further Considerations:

  • The first source, "Bar Model Method in Primary Math Only Fraction," likely contains more detailed explanations of the pedagogical principles and practical application of the bar model for different types of fraction problems. Accessing the full content of this source would provide a deeper understanding.
  • Exploring the "Other Resources" links, particularly the blog posts and other bar model tools, could offer additional perspectives and resources for educators.
  • Investigating the YouTube videos linked could provide visual demonstrations of how the bar model method is used in practice.

6. Conclusion:

The provided excerpts underscore the significance of the bar model method in primary mathematics education, particularly for teaching fractions. The development of interactive digital tools, such as the MAthematics PlaySpace applet, demonstrates a commitment to leveraging technology to enhance learning. The collaborative nature of the project and the availability of related resources suggest a strong support system for educators looking to implement this effective teaching strategy.

 

 

Bar Model Method for Fractions

Study Guide

Overview:

This study guide is designed to help you review your understanding of the bar model method for teaching and learning fractions, based on the provided sources: "Bar Model Method in Primary Math Only Fraction" and the "MAthematics PlaySpace Fractions Bar Model Interactive JavaScript Applet" resource page. The bar model method is a visual strategy that uses rectangular bars to represent whole numbers and their fractional parts, aiding in the conceptual understanding and problem-solving related to fractions.

Key Concepts to Understand:

  • Representation of Wholes: How a single bar represents a whole unit.
  • Representation of Fractions: How a bar is divided into equal parts to represent fractions (numerator and denominator).
  • Equivalent Fractions: Using bar models to visually demonstrate that different fractions can represent the same amount.
  • Comparing Fractions: Employing bar models to easily compare the relative sizes of different fractions.
  • Addition and Subtraction of Fractions: Utilizing bar models to visualize the combining or taking away of fractional parts.
  • Multiplication and Division of Fractions (Introduction): How bar models can provide an initial visual understanding of these operations.
  • The Role of Interactive Tools: Understanding how digital bar model applets can enhance learning and exploration of fraction concepts.
  • Benefits of the Bar Model Method: Recognizing the advantages of this visual approach for primary math students learning fractions.

Review Questions:

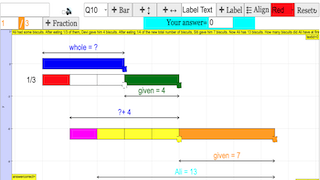
  1. What is the fundamental principle behind the bar model method for fractions? Explain how a bar is used to represent a whole and its parts.
  2. Describe how you would use a bar model to visually represent the fraction 3/5. What does the whole bar represent, and how is it divided?
  3. Explain how bar models can be used to demonstrate that 1/2 and 2/4 are equivalent fractions. What visual aspect of the models shows this equivalence?
  4. How can you use bar models to compare two fractions, such as 2/3 and 3/4? Describe the process of creating and comparing the models.
  5. Illustrate how a bar model can help solve the addition problem 1/4 + 2/4. What does the combined shaded portion of the bars represent?
  6. Explain how the "MAthematics PlaySpace Fractions Bar Model Interactive JavaScript Applet" can be a valuable tool for learning about fractions. What features or functionalities make it beneficial?
  7. According to the sources, what are some key advantages of using the bar model method in primary mathematics education for fractions? Focus on the benefits for student understanding.
  8. Briefly describe how a bar model could be used to introduce the concept of finding a fraction of a whole number (e.g., 1/3 of 12). What visual steps would be involved?
  9. How do the credits and resources mentioned in the "MAthematics PlaySpace" excerpt contribute to the credibility and utility of the applet? What kind of information do they provide?
  10. Based on the information provided, what is the intended audience or grade level for the bar model method and the interactive applet? What clues in the text suggest this?

Answer Key:

  1. The fundamental principle is the visual representation of a whole unit as a rectangle and the division of that rectangle into equal parts to represent fractions. The whole bar represents the entire quantity, while the number of equal sections indicates the denominator, and the number of shaded or selected sections indicates the numerator.
  2. To represent 3/5, a single bar is drawn to represent the whole. This bar is then divided into five equal parts, signifying the denominator of 5. Three of these five parts are then shaded or highlighted to represent the numerator of 3.
  3. To show equivalence, two identical bars are drawn. The first bar is divided into two equal parts, and one part is shaded (1/2). The second bar is divided into four equal parts, and two parts are shaded (2/4). Visually, the shaded portions of both bars should cover the same amount of the whole, demonstrating their equivalence.
  4. To compare 2/3 and 3/4, two bars of the same length are drawn. The first bar is divided into three equal parts with two shaded. The second is divided into four equal parts with three shaded. By visually comparing the shaded portions, the fraction with the larger shaded area represents the greater value. Alternatively, bars can be further divided to find a common denominator for a more precise comparison.
  5. To solve 1/4 + 2/4 with a bar model, a bar is divided into four equal parts. One part is shaded to represent 1/4. Then, two more adjacent parts are shaded to represent adding 2/4. The total shaded portion now consists of three out of the four parts, visually showing that 1/4 + 2/4 = 3/4.
  6. The interactive applet offers a dynamic and hands-on way to manipulate bar models, allowing students to visualize fractions, create equivalent fractions, and potentially perform operations. The ability to interact with the model can lead to a deeper and more intuitive understanding of fractional concepts compared to static representations.
  7. Key advantages include enhanced visual understanding of abstract fraction concepts, improved problem-solving skills by providing a concrete representation, and the facilitation of conceptual development before moving to abstract algorithms. The method helps students make connections between fractions and the whole.
  8. To show 1/3 of 12, a bar could represent the quantity 12. This bar would then be divided into three equal sections. Each section visually represents 1/3 of the whole, and the value of one of these sections (which would be 4 in this case) is the answer.
  9. The credits acknowledge the creators and contributors, lending authority to the resource. The listed "Other Resources" provide links to additional tools and information related to bar modeling and fraction learning, increasing the utility of the main applet by offering supplementary materials and alternative approaches.
  10. Based on the title's focus on "Primary Math" and the examples likely intended for initial fraction instruction, the target audience is likely elementary or primary school students learning about fractions for the first time or reinforcing their understanding.

Essay Format Questions:

  1. Discuss the significance of visual representations, such as the bar model method, in the early development of mathematical understanding, specifically focusing on the concept of fractions.
  2. Compare and contrast the use of physical manipulatives and interactive digital tools like the "MAthematics PlaySpace Fractions Bar Model Interactive JavaScript Applet" in teaching the bar model method for fractions. What are the unique advantages and disadvantages of each?
  3. Explore the different ways the bar model method can be applied to solve various types of fraction problems, including addition, subtraction, comparison, and finding a fraction of a whole. Provide examples of each.
  4. Analyze the potential challenges students might face when learning fractions and discuss how the bar model method can help address these difficulties. Consider issues such as understanding the part-whole relationship and the concept of equivalence.
  5. Based on the provided resources and your understanding, argue for the integration of the bar model method into primary mathematics curricula for fraction instruction. What evidence or pedagogical reasoning supports its effectiveness?

Glossary of Key Terms:

  • Bar Model: A visual representation using rectangular bars to represent whole numbers and their fractional parts, used as a problem-solving strategy in mathematics.
  • Fraction: A number that represents a part of a whole or, more generally, any number of equal parts. It is written as one number (numerator) over a line or slash another number (denominator).
  • Numerator: The top number in a fraction that shows how many parts of the whole are being considered.
  • Denominator: The bottom number in a fraction that shows the total number of equal parts that the whole is divided into.
  • Whole: A complete unit or quantity, represented by a single undivided bar in the bar model method.
  • Equivalent Fractions: Fractions that have different numerators and denominators but represent the same value (e.g., 1/2 and 2/4). Bar models visually demonstrate this by showing equal shaded areas for the same whole.
  • Primary Math: Mathematics taught in the early years of schooling, typically focusing on foundational concepts like whole numbers, basic operations, and introductory fractions.
  • Interactive Applet: A small, self-contained computer program or application that allows users to actively engage with and manipulate visual representations or simulations, such as the fractions bar model.
  • Visual Representation: The use of diagrams, pictures, or other visual aids to represent mathematical concepts and relationships, making them more concrete and accessible.
  • Conceptual Understanding: A deep and connected understanding of mathematical ideas, beyond just memorizing rules or procedures, allowing one to apply knowledge in different contexts.

 Video

https://www.youtube.com/watch?v=S2vAHGD1_o4 

https://www.youtube.com/watch?v=UW8EJ0M3flc 

 

Credits

CH Thong, Loo Kang WEE, Mianna Teng, Kyrin Chong

Other Resources

  1. www.ace-learning.com/model-thinking-blocks-drawing-tool-free-version as shared by Charles
  2. https://www.mathplayground.com/thinking_blocks_modeling_tool/index.html
  3. https://weelookang.blogspot.com/2021/08/mathematics-playspace-fractions.html
  4. https://mathsbot.com/manipulatives/bar
  5. https://weelookang.blogspot.com/2021/12/mathematics-playspace-fractions-bar.html

Frequently Asked Questions: Bar Model Method and Interactive Fraction Applets

1. What is the Bar Model Method in primary mathematics, particularly in relation to fractions? The Bar Model Method is a visual strategy used in primary mathematics to help students understand and solve word problems, including those involving fractions. It involves representing quantities as rectangular bars, where the length of the bar corresponds to the value. For fractions, a whole bar can represent a unit, and it can be divided into equal parts to represent fractions of that whole. This visual representation helps students to concretely see the relationships between different quantities and understand fractional concepts like parts of a whole, equivalent fractions, and operations with fractions.

2. How does the Bar Model Method aid in understanding fraction concepts? The Bar Model Method provides a concrete and visual way for students to grasp abstract fraction concepts. By seeing a whole divided into equal parts, they can understand the meaning of the numerator (the number of parts considered) and the denominator (the total number of equal parts). Comparing the lengths of different bars or sections of bars helps them visualize the relative sizes of fractions, identify equivalent fractions (by seeing if different divisions represent the same length), and understand addition and subtraction of fractions as combining or taking away sections of bars.

3. What is the MAthematics PlaySpace Fractions Bar Model Interactive JavaScript Applet? The MAthematics PlaySpace Fractions Bar Model Interactive JavaScript Applet is an online, interactive tool designed to help primary students learn about fractions using the bar model method. It allows users to dynamically manipulate bars to represent wholes and their fractional parts. This interactivity can involve dividing bars into equal segments, shading portions to represent specific fractions, and potentially comparing different fractional representations visually.

4. How can the interactive Fractions Bar Model applet be used for learning? The interactive nature of the applet allows for active learning and exploration of fraction concepts. Students can experiment with different ways of dividing a bar, visualize equivalent fractions by creating different partitions that cover the same area, and potentially model simple fraction operations. The applet can provide immediate visual feedback, reinforcing their understanding and allowing them to self-correct. Teachers can also use it as a visual aid in lessons, demonstrating fraction concepts in real-time and engaging students through interactive exercises.

5. Who developed the Bar Model Method resources and the interactive applet mentioned? The "Bar Model Method in Primary Math Only Fraction" resource and the MAthematics PlaySpace Fractions Bar Model Interactive JavaScript Applet are credited to Mianna Teng, Loo Kang Wee, and kyrin. They are associated with Open Educational Resources / Open Source Physics @ Singapore.

6. Are there other digital tools or resources related to the Bar Model Method and fractions available? Yes, the provided sources mention several other resources related to visual modeling in mathematics, including:

7. Is there video support available for understanding or using these resources? Yes, the MAthematics PlaySpace Fractions Bar Model Interactive JavaScript Applet page includes links to two YouTube videos: https://www.youtube.com/watch?v=S2vAHGD1_o4 and https://www.youtube.com/watch?v=UW8EJ0M3flc. These videos likely provide demonstrations or explanations on how to use the applet and potentially how the bar model method can be applied to understanding fractions.

8. What are some of the key features or functionalities that might be included in an interactive Fractions Bar Model applet? Based on the "About" section of the applet, potential features include the ability to create and manipulate bars representing wholes, divide these bars into equal parts, shade or color specific fractional portions, and possibly interact with "related" arrows and boxes to represent relationships between different fractions or quantities. Future development considerations include adding label input boxes to further customize the representations. The goal is to provide a dynamic and visual environment for exploring and understanding fraction concepts through the bar model method.

3.5 1 1 1 1 1 1 1 1 1 1 Rating 3.50 (3 Votes)
Details
Parent Category: Whole Numbers
Category: 1. Numbers up to 100
Hits: 3333