About
Bungee Oscillation
Activities
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits



 Leong Tze Kwang; Lawrence Wee Loo Kang; Francisco Esquembre; Felix Garcia Clemente
Leong Tze Kwang; Lawrence Wee Loo Kang; Francisco Esquembre; Felix Garcia Clemente
1. Overview:
This document reviews the information provided on the "Horizontal spring dynamics HTML5 Applet Javascript" webpage hosted by Open Educational Resources / Open Source Physics @ Singapore. The page introduces an interactive simulation designed to demonstrate the dynamics of a mass attached to a horizontal spring. It highlights the availability of the simulation as an open educational resource, its alignment with Newtonian Mechanics and the topic of oscillations, and provides information for embedding and utilizing the applet for learning and teaching.
2. Main Themes and Important Ideas:
- Interactive Physics Simulation: The core of the resource is an embeddable HTML5 applet built with Javascript that simulates the behavior of a mass connected to a horizontal spring. The embed code provided (<iframe width="100%" height="100%" src="https://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_horizontalspring_dynamics/horizontalspring_dynamics_Simulation.xhtml " frameborder="0"></iframe>) allows users to integrate this dynamic model directly into their own webpages.
- Open Educational Resource (OER) / Open Source Physics: The webpage is presented under the banner of "Open Educational Resources / Open Source Physics @ Singapore," emphasizing its commitment to freely accessible and reusable educational materials. The licensing information at the bottom ("Contents are licensed Creative Commons Attribution-Share Alike 4.0 Singapore License") reinforces this. The mention of the "EasyJavaScriptSimulations Library" and its specific commercial use license further clarifies the open-source nature of the underlying tools.
- Focus on Newtonian Mechanics and Oscillations: The applet is explicitly categorized under "Newtonian Mechanics" and "Physics," specifically within the subtopic of "Dynamics" and related to "oscillations." This indicates its pedagogical purpose in illustrating fundamental physics principles related to force, mass, and motion in the context of oscillatory systems.
- Learning Activities and Sample Goals: The page includes sections titled "Activities" and "Sample Learning Goals" (though the latter contains "[texthttps://weelookang.blogspot.com/2020/07/horizontal-spring-dynamics-html5-applet.html) suggests a history of development and potential updates to the simulation.
- Integration with Other Resources: The presence of "Other Resources" (again, marked as "[texthttps://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_horizontalspring_dynamics/horizontalspring_dynamics_Simulation.xhtml " frameborder="0"></iframe>
- (For Teachers - Potential Activities):"Drag the mass and observe the force exerted by the spring on the cart"
- "Changing of variables - maximum spring constant,k and minimum mass, m"
- "Changing of variables - minimum spring constant, k and maximum mass, m"
- (Credits): "Leong Tze Kwang; Lawrence Wee Loo Kang; Francisco Esquembre; Felix Garcia Clemente"
- (License Information): "Contents are licensed Creative Commons Attribution-Share Alike 4.0 Singapore License"
4. Conclusion:
The "Horizontal spring dynamics HTML5 Applet Javascript" page provides access to a valuable open educational resource for teaching and learning about the dynamics of horizontal spring systems. The embeddable simulation allows for interactive exploration of the relationship between force, mass, and oscillation. The resource is part of a larger initiative focused on open-source physics education in Singapore, offering a wide range of interactive models and tools for educators and learners. The identified learning activities and the "For Teachers" section highlight the pedagogical intent behind this resource. Further exploration of the linked version and the broader website would likely reveal more specific learning goals and supporting materials.
Horizontal Spring Dynamics Study Guide
Overview
This study guide focuses on the "Horizontal spring dynamics HTML5 Applet Javascript" resource from Open Educational Resources / Open Source Physics @ Singapore. The resource provides an interactive simulation to explore the concepts of Newtonian mechanics and oscillations, specifically in the context of a mass attached to a horizontal spring.
Key Concepts
- Newtonian Mechanics: The fundamental laws of motion, including inertia, force, and acceleration.
- Oscillation: A repetitive variation, typically in time, about a central value or between two or more different states.
- Horizontal Spring System: A system consisting of a mass attached to a spring that moves back and forth on a frictionless horizontal surface.
- Force Exerted by a Spring (Hooke's Law): The force needed to extend or compress a spring by a distance x is proportional to that distance (F = -kx), where k is the spring constant.
- Spring Constant (k): A measure of the stiffness of a spring; a higher spring constant indicates a stiffer spring.
- Mass (m): A measure of the amount of matter in an object, which influences its inertia.
- Equilibrium Position: The position where the spring is neither stretched nor compressed, and the net force on the mass is zero.
- Displacement (x): The distance of the mass from its equilibrium position.
- Maximum Displacement (Amplitude): The maximum distance the mass moves from its equilibrium position during an oscillation.
- Effect of Changing Variables: Understanding how changing the spring constant (k) and the mass (m) affects the behavior of the oscillating system (though the specifics aren't detailed in this excerpt).
Review Questions
Short Answer Quiz
- What fundamental area of physics does the horizontal spring dynamics applet primarily explore?
- According to the information provided, what happens when you drag the mass in the simulation?
- State Hooke's Law in your own words and identify the key variables involved.
- What does a higher value for the spring constant (k) indicate about the spring?
- What physical property of the cart does the variable 'm' represent in the context of the simulation?
- Describe the equilibrium position in a horizontal spring system.
- What is meant by the term "oscillation" as it relates to the horizontal spring system?
- Based on the "Changing of variables" points, what two properties of the system can be adjusted in the simulation?
- What is the purpose of the embedded iframe link provided in the resource?
- Who are some of the key individuals credited for the development of this resource?
Short Answer Quiz - Answer Key
- The horizontal spring dynamics applet primarily explores Newtonian Mechanics and Oscillations.
- When you drag the mass in the simulation, you can observe the force exerted by the spring on the cart change as the spring is stretched or compressed.
- Hooke's Law states that the force exerted by a spring is proportional to the amount it is stretched or compressed from its equilibrium position; the key variables are force (F), spring constant (k), and displacement (x).
- A higher value for the spring constant (k) indicates that the spring is stiffer and requires more force to stretch or compress by a given distance.
- The variable 'm' represents the mass of the cart, which affects its inertia and how it responds to the force exerted by the spring.
- The equilibrium position in a horizontal spring system is the point where the spring is neither stretched nor compressed, resulting in no net force acting on the mass.
- Oscillation in this context refers to the back-and-forth motion of the mass attached to the spring around its equilibrium position.
- Based on the provided information, the two properties of the system that can be adjusted in the simulation are the maximum and minimum spring constant (k) and the minimum and maximum mass (m).
- The embedded iframe link allows users to directly integrate and run the horizontal spring dynamics simulation within another webpage.
- Some of the key individuals credited for the development of this resource include Leong Tze Kwang, Lawrence Wee Loo Kang, Francisco Esquembre, and Felix Garcia Clemente.
Essay Format Questions
- Explain how the concepts of force, mass, and acceleration, as described by Newton's Laws of Motion, are relevant to the behavior of a mass attached to a horizontal spring undergoing oscillation.
- Discuss the relationship between the spring constant (k) and the oscillatory motion of the mass. How would increasing or decreasing the spring constant affect the system's behavior? (Note: While not explicitly detailed, consider how stiffness generally influences oscillations).
- Hypothesize about the effect of changing the mass (m) attached to the spring on the characteristics of its oscillation. Explain your reasoning based on fundamental physics principles.
- The resource highlights the ability to change variables such as the maximum and minimum spring constant and mass. Describe how experimenting with these variables in the simulation could enhance understanding of horizontal spring dynamics.
- Beyond the horizontal spring, what other real-world systems exhibit oscillatory behavior that might be understood through similar physics principles? Provide a few examples and briefly explain the analogy.
Glossary of Key Terms
- Newtonian Mechanics: A set of physical laws describing the relationship between the motion of an object and the forces acting upon it.
- Oscillation: A repetitive variation over time of some measure about a central value or between two or more different states.
- Spring Constant (k): A measure of a spring's stiffness, defined as the force per unit extension or compression.
- Mass (m): A fundamental property of an object that measures its resistance to acceleration when a net force is applied.
- Equilibrium Position: The state in which opposing forces or influences are balanced, and in the context of a spring, where it is neither stretched nor compressed.
- Displacement (x): The vector quantity that describes the distance and direction of an object from its equilibrium position.
- Hooke's Law: A law stating that the force needed to extend or compress a spring by a distance is proportional to that distance (F = -kx).
- Amplitude: The maximum displacement or distance moved by a point on a vibrating body or wave measured from its equilibrium position.
- Damping (Not explicitly in source but relevant to oscillations): A force that opposes the motion in an oscillatory system, causing the amplitude of the oscillations to decrease over time.
- Frequency (Not explicitly in source but relevant to oscillations): The number of oscillations that occur per unit of time.
Sample Learning Goals
[text]
For Teachers
| Initial setup |
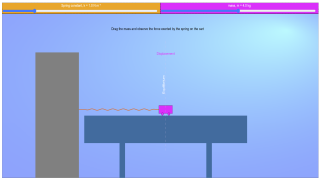
Drag the mass and observe the force exerted by the spring on the cart |
| Changing of variables - minimum spring constant, k and maximum mass, m |
Research
[text]
Video
[text]
Version:
1. https://weelookang.blogspot.com/2020/07/horizontal-spring-dynamics-html5-applet.html
Other Resources
Frequently Asked Questions: Horizontal Spring Dynamics Applet
- What is the purpose of the Horizontal Spring Dynamics HTML5 Applet? The applet is an interactive simulation designed to demonstrate and explore the dynamics of a mass attached to a horizontal spring, likely illustrating concepts related to Newtonian mechanics and oscillations. Users can interact with the simulation, likely by dragging the mass and observing the resulting motion and forces exerted by the spring.
- What physics concepts can be explored using this applet? Based on its categorization under "Newtonian Mechanics" and "Dynamics," this applet likely allows users to investigate principles such as Hooke's Law (the relationship between the spring force and displacement), simple harmonic motion, the effect of mass and spring constant on the period and frequency of oscillations, and the transfer of energy in an oscillating system.
- How can users interact with the Horizontal Spring Dynamics Applet? The "Images: Initial setup" and "Drag the mass and observe the force exerted by the spring on the cart" descriptions suggest that users can directly manipulate the mass in the simulation, likely by clicking and dragging it from its equilibrium position. This action would then initiate the oscillatory motion, allowing observation of the resulting dynamics.
- What variables can be changed within the simulation? The "Changing of variables - maximum spring constant, k and minimum mass, m" and "Changing of variables - minimum spring constant, k and maximum mass, m" points indicate that users can adjust the values of the spring constant (k) and the mass (m) attached to the spring. By changing these parameters, users can observe their impact on the system's behavior.
- Is this applet intended for a specific educational level? While not explicitly stated, the inclusion under "Open Educational Resources / Open Source Physics @ Singapore" and the sample learning goals (mentioned as "[texthttps://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_horizontalspring_dynamics/horizontalspring_dynamics_Simulation.xhtml) directly links to the simulation. Additionally, Version 1 is linked to a blog post (https://weelookang.blogspot.com/2020/07/horizontal-spring-dynamics-html5-applet.html), which likely provides further context and information about the applet.
- Details
- Written by Coco Lee
- Parent Category: Physics
- Category: 02 Newtonian Mechanics
- Hits: 5638