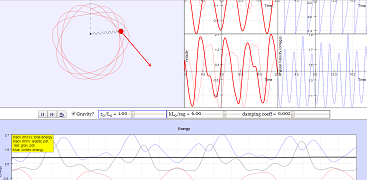
About

Mass on a Spring: Motion in a Vertical Plane

A mass m is situated at the end of a spring of (unstretched) length L₀ and negligible mass. The spring is fixed at the other end and the motion is restricted to two spatial dimensions in a vertical plane, with the y-axis representing the vertical (if gravity is switched on).

We use Hooke's law (with spring constant k) for the spring force, and include a damping term that is proportional to the velocity of the mass. You can also choose for the spring to behave like a spring only when stretched, and have no effect when compressed (i.e. it is more like a string).

Applying Newton's Second Law yields a second-order ordinary differential equation, which we solve numerically in the simulation and visualise the results.

Activities

1. Drag the red mass to impart an initial velocity, and see how the system evolves.
2. Try changing the initial vertical position of the mass relative to the fixed end of the spring using the slider.
3. Observe what happens when gravity is switched off.
4. Try varying the spring constant relative to the force of gravity and/or the damping coefficient, using the sliders. You may need to fiddle with the damping coefficient to better approximate energy conservation.
5. Also try activating the "string-like" mode such that the elastic force only occurs in the stretched state and not in the compressed state.

 

Translations

Code	Language		Translator	Run

Credits

Wolfgang Christian; Francisco Esquembre; Zhiming Darren TAN

Overview:

These sources describe an interactive HTML5 JavaScript simulation designed for educational purposes, specifically to explore the motion of a mass attached to a spring under the influence of gravity. The simulation allows users to manipulate various parameters and observe the resulting behavior of the system in a vertical plane. It is part of the Open Source Physics (OSP) project and is aimed at students from junior college level and above, particularly those studying physics concepts like gravity, oscillations, and rotational motion (though the focus here is primarily on the first two).

Main Themes and Important Ideas/Facts:

1. Interactive Simulation for Physics Education:

• The core idea is to provide a visual and interactive tool to understand the abstract concepts of mass-spring systems and the effect of gravity on their motion. The simulation is described as a "Mass and Spring in Gravity HTML5 JavaScript Simulation".
• It is explicitly mentioned as an "Open Educational Resource" from "Open Source Physics @ Singapore", highlighting its accessibility and free use for educational purposes.
• The inclusion of an embed code (<iframe width="100%" height="100%" src="https://iwant2study.org/lookangejss/physicszdtan/ejss_model_MassAndSpringStringGravity/MassAndSpringStringGravity_Simulation.xhtml " frameborder="0"></iframe>) emphasizes its usability within online learning environments and webpages.

2. Modeling Mass-Spring Motion in a Vertical Plane with Gravity:

• The simulation models a mass (m) attached to a spring with an unstretched length (L0) and negligible mass.
• The motion is constrained to two spatial dimensions in a vertical plane, with the y-axis representing the vertical direction where gravity acts.
• The simulation incorporates key physical principles:
• Hooke's Law: Used to model the spring force, dependent on the spring constant (k) and the displacement from the equilibrium position.
• Gravity: Included when switched on, acting vertically on the mass.
• Damping: A term proportional to the velocity of the mass can be included to model energy dissipation.
• The underlying physics is governed by Newton's Second Law, which results in a "second-order ordinary differential equation" that is solved numerically within the simulation.

3. Simulation Features and User Interactivity:

• The "Activities" section details how users can interact with the simulation:
• Initial Velocity: Users can "drag the red mass to impart an initial velocity, and see how the system evolves."
• Initial Vertical Position: A "slider" allows users to "try changing the initial vertical position of the mass relative to the fixed end of the spring."
• Gravity Control: Users can "observe what happens when gravity is switched off." This allows for comparison of motion with and without gravitational influence.
• Parameter Variation: Sliders are available to "try varying the spring constant relative to the force of gravity and/or the damping coefficient." This enables exploration of how these parameters affect the system's behavior.
• "String-like" Mode: A feature allows the spring to "behave like a spring only when stretched, and have no effect when compressed (i.e. it is more like a string)." This introduces non-linearity to the system.

4. Pedagogical Goals and Applications:

• The simulation aims to help students visualize and understand the interplay between spring force and gravitational force, leading to oscillatory motion.
• The ability to adjust parameters and observe the effects supports inquiry-based learning and the development of intuitive understanding.
• The mention of "Junior College" and "H3 Physics" suggests the intended audience and the level of physics concepts that can be explored.
• The inclusion of "Sample Learning Goals" (though the text is "[texthttps://www.um.es/fem/EjsWiki/) provides further context about the underlying technology and the broader OSP ecosystem.
• The recognition of the Open Source Physics Team with the "2020 Excellence in Physics Education Award from American Physical Society" underscores the impact and quality of their work in physics education.

6. Broader Context within Open Educational Resources @ Singapore:

• The simulation is presented within a larger repository of open educational resources, as evidenced by the "Breadcrumbs" and the extensive list of other simulations and resources available on the platform. This suggests a rich environment for exploring various physics and other science concepts.
• The listing includes a wide range of interactive simulations covering topics from rotational motion to electromagnetism, and even games for learning languages and mathematics, demonstrating the breadth of the OER platform.

Key Quotes:

• From the simulation page title: "Mass and Spring in Gravity HTML5 JavaScript Simulation by Darren Z Tan - Open Educational Resources / Open Source Physics @ Singapore" - This clearly states the topic, format, creator, and source.
• From the "About" section: "A mass m is situated at the end of a spring of (unstretched) length L0 and negligible mass. The spring is fixed at the other end and the motion is restricted to two spatial dimensions in a vertical plane, with the y-axis representing the vertical (if gravity is switched on)." - This describes the fundamental setup of the modeled system.
• From the "About" section: "We use Hooke's law (with spring constant k ) for the spring force, and include a damping term that is proportional to the velocity of the mass." - This identifies the key forces and physical laws included in the model.
• From the "Activities" section: "Drag the red mass to impart an initial velocity, and see how the system evolves." - This is an example of the interactive elements offered to users.
• The embed code provides a direct way to integrate the simulation into other online platforms, highlighting its accessibility.

Conclusion:

The "Mass and Spring in Gravity" HTML5 JavaScript simulation is a valuable open educational resource for teaching and learning about the dynamics of a mass-spring system under the influence of gravity. Its interactive features allow students to explore the effects of various parameters, fostering a deeper understanding of the underlying physical principles. The simulation is part of the broader Open Source Physics project, emphasizing its commitment to free and accessible physics education. The detailed description and interactive capabilities make it a useful tool for educators at the junior college level and potentially beyond.

 

Mass and Spring in Gravity Study Guide

Key Concepts:

• Hooke's Law: The force needed to extend or compress a spring by a distance x is proportional to that distance. Mathematically, it is expressed as F = -kx, where F is the spring force, k is the spring constant, and x is the displacement from the equilibrium position.
• Newton's Second Law: The acceleration of an object is directly proportional to the net force acting on the object, is in the same direction as the net force, and is inversely proportional to the mass of the object (F_net = ma).
• Gravity: The force that attracts any two objects with mass towards each other. Near the Earth's surface, the force of gravity on an object of mass m is given by F_g = mg, where g is the acceleration due to gravity (approximately 9.8 m/s²).
• Oscillation: A repetitive variation, typically in time, of some measure about a central value or between two or more different states.
• Damping: A force that opposes motion and reduces the amplitude of oscillations in a system over time. The damping force is often proportional to the velocity of the object.
• Equilibrium Position: The position of an object where the net force acting on it is zero. In a mass-spring system under gravity, this is where the spring force balances the gravitational force.
• Restoring Force: A force that acts to bring a system back to its equilibrium position. In a mass-spring system, both the spring force and gravity (in the vertical direction) contribute to the restoring force when the mass is displaced from equilibrium.
• Potential Energy (Elastic): The energy stored in a spring when it is stretched or compressed, given by PE_elastic = (1/2)kx².
• Potential Energy (Gravitational): The energy an object possesses due to its position in a gravitational field, given by PE_gravitational = mgy (relative to some reference point).
• Kinetic Energy: The energy an object possesses due to its motion, given by KE = (1/2)mv².
• Energy Conservation: In a closed system without non-conservative forces (like damping), the total mechanical energy (the sum of potential and kinetic energy) remains constant.

Short-Answer Quiz:

1. State Hooke's Law in your own words and provide the mathematical formula. Explain what each variable in the formula represents.
2. How does the presence of gravity affect the equilibrium position of a mass hanging from a spring compared to a horizontal mass-spring system?
3. Describe the role of the spring constant (k) in the oscillatory motion of a mass-spring system. How does a larger k value influence the oscillations?
4. What is damping, and how does it affect the motion of a mass-spring system over time? Provide an example of a damping force.
5. Explain the difference in the spring's behavior when the simulation is switched to "string-like" mode. How does this affect the possible motion of the mass?
6. According to Newton's Second Law, what is the relationship between the net force acting on the mass and its acceleration in the vertical plane? Identify the forces acting on the mass in this system.
7. Describe one activity suggested by the simulation that allows you to observe the principles of energy conservation (or energy dissipation) in the mass-spring system.
8. How would the oscillatory motion of the mass change if gravity were switched off in the simulation? Explain your reasoning.
9. What type of differential equation is mentioned as being used to model the motion of the mass on the spring, and why is numerical solving necessary?
10. Briefly explain how you could use the simulation to investigate the relationship between the initial conditions (position and velocity) of the mass and the resulting oscillatory motion.

Answer Key:

1. Hooke's Law states that the force exerted by a spring is directly proportional to the amount it is stretched or compressed and acts in the opposite direction of the displacement. The formula is F = -kx, where F is the spring force, k is the spring constant (a measure of the spring's stiffness), and x is the displacement from the spring's equilibrium length.
2. In a horizontal mass-spring system, the equilibrium position is where the spring is at its unstretched length. However, in a vertical system under gravity, the equilibrium position is lower because the spring must stretch enough so that its upward force balances the downward force of gravity on the mass (kΔy = mg).
3. The spring constant (k) represents the stiffness of the spring. A larger k means a stiffer spring that requires more force to stretch or compress by a given distance. A larger k results in a higher frequency of oscillation, meaning the mass oscillates more rapidly.
4. Damping is a force that opposes the motion of an oscillating system and causes the amplitude of the oscillations to decrease over time. It dissipates mechanical energy, often as heat. An example of a damping force in this context is the velocity-proportional damping term mentioned in the description.
5. In "string-like" mode, the spring only exerts a restoring force when it is stretched. When compressed, it provides no force, acting like a slack string. This restricts the motion, preventing the mass from being pushed upwards by the spring beyond its unstretched length.
6. Newton's Second Law states that the net force on the mass is equal to its mass times its acceleration (F_net = ma). In the vertical plane, the forces acting on the mass are the spring force (given by Hooke's Law), the gravitational force acting downwards, and the damping force opposing its velocity.
7. Activity 4, which involves varying the damping coefficient, allows observation of energy conservation (when damping is minimal and oscillations persist with roughly constant amplitude) versus energy dissipation (when significant damping causes the oscillations to die out). Fiddling with the damping coefficient to approximate energy conservation implies minimizing energy loss.
8. If gravity were switched off, the equilibrium position would revert to the unstretched length of the spring (in the vertical orientation described). The oscillations would be purely due to the spring force around this new equilibrium, and the frequency would be determined solely by the mass and the spring constant.
9. The motion is modeled by a second-order ordinary differential equation because it involves acceleration (the second derivative of position with respect to time) and depends on forces that are functions of position and velocity. Numerical solving is often necessary because these differential equations can be complex and may not have simple analytical solutions, especially with the inclusion of damping and the "string-like" behavior.
10. By using Activity 1 (dragging the mass to impart an initial velocity) and Activity 2 (changing the initial vertical position), one can set different starting conditions for the mass. Observing the resulting oscillations in each case will reveal how the initial displacement and velocity influence the amplitude, frequency, and overall trajectory of the motion.

Essay Format Questions:

1. Discuss the interplay between Hooke's Law and Newton's Second Law in determining the oscillatory motion of a mass-spring system, both in the absence and presence of gravity. How does gravity modify the system's behavior?
2. Analyze the role of energy conservation and energy dissipation (due to damping) in the mass-spring system. How do changes in the spring constant and damping coefficient affect the total mechanical energy of the system over time?
3. Compare and contrast the behavior of the mass-spring system when the spring acts as a traditional spring versus when it is constrained to behave like a string (only providing tension). What are the implications of this change for the types of motion observed?
4. Explain how the provided simulation can be used as a tool for understanding the concept of equilibrium in a physical system. Discuss how different parameters (mass, spring constant, gravity) affect the equilibrium position of the mass.
5. Describe how the activities suggested in the simulation allow for the exploration of fundamental physics principles such as force, motion, and energy in the context of a mass-spring system under the influence of gravity. Provide specific examples from the activities.

Glossary of Key Terms:

• Amplitude: The maximum displacement or distance moved by a point on a vibrating body or wave measured from its equilibrium position.
• Damping Coefficient: A measure of the strength of the damping force in an oscillatory system. A higher damping coefficient leads to faster decay of oscillations.
• Frequency: The number of oscillations or cycles that occur per unit of time, typically measured in Hertz (Hz).
• Period: The time taken for one complete oscillation or cycle. It is the inverse of the frequency.
• Spring Constant (k): A measure of the stiffness of a spring, defined as the force per unit extension or compression. Measured in Newtons per meter (N/m).
• Tension: The pulling force exerted by a stretched string, cable, or similar object on another object to which it is attached.
• Trajectory: The path followed by an object moving through space.
• Unstretched Length (L0): The length of a spring when no external force is applied to it.
• Velocity: The rate of change of an object's position with respect to time, including both speed and direction.
• Vertical Plane: A two-dimensional plane oriented in such a way that it includes the direction of gravity.

Sample Learning Goals

[text]

For Teachers

[text]

Research

[text]

Video

[text]

 Version:

1. https://weelookang.blogspot.com/2020/10/mass-and-spring-in-gravity-html5.html

Other Resources

[text]