About
Using The Beach Ball Physics Model
 The physics of a thrown beach ball can be very interesting. Because of
its relatively low mass (compared to its size), subtle effects that are
important in sports like baseball, soccer and volleyball become
exaggerated in the beach ball’s motion. This simulation allows users to
explore a simple model of several “complications” to simple projectile
motion: drag, buoyancy and the Magnus effect. Drag slows the ball down,
buoyancy makes the ball “float” and the Magnus effect puts a curve on
the ball’s trajectory.
The physics of a thrown beach ball can be very interesting. Because of
its relatively low mass (compared to its size), subtle effects that are
important in sports like baseball, soccer and volleyball become
exaggerated in the beach ball’s motion. This simulation allows users to
explore a simple model of several “complications” to simple projectile
motion: drag, buoyancy and the Magnus effect. Drag slows the ball down,
buoyancy makes the ball “float” and the Magnus effect puts a curve on
the ball’s trajectory.
Simulation Controls:
The simulations main display includes an interactive 3-D display of the ball in flight. The “Show Velocity” checkbox will add a pair of vectors for the ball’s velocity and angular velocity (both scaled to the ball’s launch speed). The “Show Forces” checkbox adds vectors for all the forces contributing to the ball’s dynamics. A pair of graphs may be hidden or viewed for ancillary information using the Show Graphs checkbox.
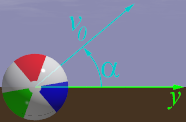 The basic ball launch parameters are the initial height of the ball, the
launch speed and the launch angle α (from horizontal).
The basic ball launch parameters are the initial height of the ball, the
launch speed and the launch angle α (from horizontal).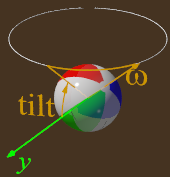
Beach Balls come in various sizes, so the radius and mass of the ball can be specified. Note that the assumption is that the mass given is what would be measured on a balance; the mass of the air inside the ball does not affect such measurements as its weight is offset by the buoyancy due to the displaced volume of air. To see the buoyant force in a simple way, note that if you weigh your beach ball empty or inflated, you will get the same measurement and yet the inflated ball’s contents do contribute to the overall inertia.
The simulation also allows the adjustment of some of the aerodynamic parameters. See the technical notes for discussion. For those interested in the aerodynamics, the Reynolds number and Spin factor are also displayed.
The Physics of Beach Ball Trajectories: Technical Notes
The model employed in this simulation follows Clanet’s “Sports Ballistics”.1 This simulation takes up as the positive z direction and the initial velocity of the ball to be in the y-z plane.
Gravity and Buoyancy
In a Physics Teacher paper on the vertical motion accounting for aerodynamic effects, Timmerman and van der Weele2 note
The mass (and hence the weight) of a beach ball are easy to determine: just place it on an electronic balance. The same results will be obtained whether the ball is inflated or not. When a ball is thrown, the air inside goes for a ride as well, and in the case of a beach ball, this is a significant contribution to inertia:
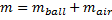
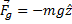
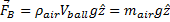
Drag Force
Drag force, or air resistance is the friction effect of moving though the air. It will be a significant force for almost any toss of the beach ball. The drag force is opposes motion and it is modeled in this simulation by
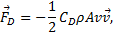 ,
,

Magnus Effect
The Magnus force is very noticeable when it is used to make the trajectory of a ball curve while in flight. The size of the effect depends upon both the velocity and angular velocity of the ball, and the direction is always perpendicular to both the velocity and the rotation axis of the ball’s spin. The force is often referred to as lift, and (following Clanet) is given by:
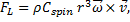
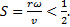
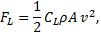
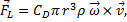
Complete Model Dynamics
The full beach ball dynamics used in the model is given by
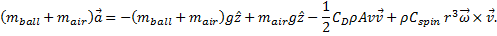
(1) Sports Ballistics by Clanet, Christophe, Annual Review of Fluid Mechanics, 01/2015, Volume 47, Issue 1
(2) On the rise and fall of a ball with linear or quadratic drag by Timmerman, Peter; Weele, van der, Jacobus P, American Journal of Physics, 1999, Volume 67, Issue 6
(3) For more information on drag, see https://en.wikipedia.org/wiki/Drag_coefficient
(4) Nathan AM. 2008. The effect of spin on the flight of a baseball. Am. J. Phys. 76:119–24
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits

 Michael R. Gallis, Ryan Vidal; lookang
Michael R. Gallis, Ryan Vidal; lookang
Overview
This briefing document summarizes the key aspects of an interactive JavaScript simulation designed to explore the physics of a thrown beach ball, contrasting it with the motion of other sports balls. The simulation emphasizes the exaggerated effects of drag, buoyancy, and the Magnus effect on beach balls due to their low mass relative to their size. It serves as an open educational resource for physical and sports education.
Main Themes and Important Ideas/Facts
1. Exaggerated Physics of Beach Ball Trajectories:
- The core theme is that beach balls, due to their physical properties (low mass, large size), exhibit exaggerated aerodynamic effects compared to denser sports balls like baseballs or tennis balls.
- The simulation allows users to visualize and understand these "complications" to simple projectile motion: drag, buoyancy, and the Magnus effect.
- Quote: "The physics of a thrown beach ball can be very interesting. Because of its relatively low mass (compared to its size), subtle effects that are important in sports like baseball, soccer and volleyball become exaggerated in the beach ball’s motion."
2. Key Aerodynamic Forces:
- Drag: This force opposes the motion of the ball through the air and is modeled in the simulation. The drag coefficient for a beach ball is noted to be typically around 0.5, higher than that of smoother, denser sports balls.
- Quote: "Drag force, or air resistance is the friction effect of moving though the air. It will be a significant force for almost any toss of the beach ball. The drag force is opposes motion and it is modeled in this simulation by [mathematical equation for drag force]."
- Buoyancy: The buoyant force, often ignored in discussions of sports ballistics, is included in the model. It is the upward force exerted by the air displaced by the ball. The source highlights that while the air inside the beach ball contributes significantly to its inertia, its weight is offset by buoyancy, leading to the same measured mass whether inflated or not.
- Quote: "…we include the buoyant force, which is almost always forgotten or ignored in the literature on this topic. This is somewhat curious, since the medium that is responsible for the drag force at the same time introduces a buoyant force.”
- Quote: "Note that the assumption is that the mass given is what would be measured on a balance; the mass of the air inside the ball does not affect such measurements as its weight is offset by the buoyancy due to the displaced volume of air. To see the buoyant force in a simple way, note that if you weigh your beach ball empty or inflated, you will get the same measurement and yet the inflated ball’s contents do contribute to the overall inertia."
- Magnus Effect: This force causes the ball's trajectory to curve due to its spin. The direction of the Magnus force is perpendicular to both the velocity and the spin axis. The simulation allows users to explore different spin rates and axis orientations to observe various curveball effects and floating motions.
- Quote: "The Magnus force is very noticeable when it is used to make the trajectory of a ball curve while in flight. The size of the effect depends upon both the velocity and angular velocity of the ball, and the direction is always perpendicular to both the velocity and the rotation axis of the ball’s spin."
3. Simulation Features and Controls:
- The simulation provides an interactive 3D display of the ball in flight.
- Users can toggle the display of velocity and angular velocity vectors, as well as the vectors for all contributing forces (gravity, buoyancy, drag, Magnus).
- Ancillary graphs can be shown or hidden.
- Key launch parameters are adjustable: initial height, launch speed, and launch angle.
- Detailed control over the ball's spin is provided: spin rate (rotations per second), tilt of the spin axis relative to horizontal, and azimuthal angle of the spin axis. Presets for simple curve balls, floating effects (backspin), and top spin sinkers are suggested.
- Users can modify the physical properties of the beach ball: radius and mass.
- Aerodynamic parameters can also be adjusted (refer to technical notes for details).
- The simulation displays the Reynolds number and Spin factor, relevant for understanding the aerodynamic regime.
4. Underlying Physics Model:
- The model is based on Clanet's "Sports Ballistics."
- The simulation considers the positive z-direction as upward and the initial velocity to be in the y-z plane.
- The complete dynamics incorporate gravity, buoyancy, drag, and the Magnus force.
- Quote: "The full beach ball dynamics used in the model is given by [mathematical equation for complete dynamics]."
5. Caveats and Limitations:
- The technical notes mention that drag and lift models become more complex at high Reynolds numbers (around 10^5), known as the "drag crises."
- The authors caution that while the model is sophisticated compared to simple projectile motion, high-fidelity results across all launch conditions should not be guaranteed.
- Quote: "Bottom line: as sophisticated as this model is compared to drag-free ballistic motion, one should still not necessarily expect high fidelity results over all launch conditions."
6. Sample Learning Outcomes (Inferred from Questions):
- Understanding how backspin and topspin affect the trajectory and distance traveled by a ball.
- Visualizing the effect of left spin on the horizontal and depth components of a ball's trajectory.
- Relating the type of spin to the speed at which a ball reaches the ground.
7. Resources and Context:
- The page includes links to technical notes, translations, credits, sample learning goals, resources for teachers, and relevant videos.
- It is part of a larger collection of open educational resources in physics from Singapore.
- The inclusion of numerous other interactive simulations on the website highlights the project's commitment to providing diverse learning tools.
Quotes Highlighting Key Concepts:
- On Buoyancy: "For most balls used in sports (baseball, soccer, volleyball, etc.) the buoyant force and the inertia of the air contained within the ball are ignorable." (This contrasts with the beach ball where it is significant.)
- On Magnus Force Formulation: "An alternate (and more common) formulation of the Magnus force is given by [mathematical equation] which, with the cross section area A=π r2 and the lift coefficient CL=2 CD S, the Magnus force would be then be written in vector form as: [mathematical equation] Which corresponds to Clanet form and typical Cspin when CD≈.5." (Demonstrates the connection between different models of the Magnus force.)
Conclusion
This simulation provides a valuable interactive tool for understanding the complex physics governing the trajectory of a beach ball. By allowing users to manipulate various parameters and visualize the contributing forces, it effectively demonstrates the significant roles of drag, buoyancy, and the Magnus effect, particularly in scenarios where the object has a low mass-to-size ratio. The resource is well-documented, provides theoretical background, and suggests avenues for exploration, making it a useful asset for physical and sports education.
Study Guide: Physics of Beach Ball Trajectories
Overview
This study guide is designed to help you review the physics principles governing the motion of a beach ball as described in the provided sources. The focus is on understanding how factors like drag, buoyancy, and the Magnus effect influence a beach ball's trajectory, contrasting it with simpler projectile motion and sports balls with different properties.
Key Concepts to Understand
- Projectile Motion: The basic parabolic path an object follows under the influence of gravity alone.
- Drag Force (Air Resistance): The force that opposes the motion of an object through the air, dependent on factors like the object's shape, size, speed, and the air's density.
- Buoyant Force: The upward force exerted by a fluid (in this case, air) that opposes the weight of an immersed object. It is equal to the weight of the fluid displaced by the object.
- Magnus Effect: The force exerted on a spinning object moving through a fluid, perpendicular to both the velocity and the axis of rotation. This force can cause the trajectory of the ball to curve.
- Spin: The rotation of the ball, characterized by its rate (rotations per second) and the orientation of its spin axis (tilt and azimuth).
- Velocity: The speed and direction of the ball's motion.
- Angular Velocity: The rate at which the ball is rotating.
- Reynolds Number: A dimensionless quantity that describes the ratio of inertial forces to viscous forces within a fluid. It helps predict flow patterns and affects drag.
- Spin Factor: A dimensionless parameter related to the ratio of the ball's surface speed due to spin to its translational speed, influencing the Magnus force.
- Newtonian Mechanics: The fundamental principles of motion based on Newton's laws.
- Inertia: The tendency of an object to resist changes in its state of motion.
- Weight: The force of gravity acting on an object's mass.
Quiz: Short Answer Questions
Answer each question in 2-3 sentences based on the provided sources.
- Why are the effects of drag, buoyancy, and the Magnus effect more pronounced on a beach ball compared to a baseball?
- Describe how the "Show Velocity" and "Show Forces" checkboxes in the simulation can help users understand the forces acting on the beach ball.
- Explain how to set the simulation parameters to observe a simple curve ball trajectory.
- According to the text, why does the measured mass of a beach ball on a balance remain the same whether it is empty or inflated?
- What is the direction of the drag force relative to the motion of the beach ball? How is it modeled in the simulation?
- How does the Magnus effect influence the trajectory of a spinning beach ball? What two factors determine the size and direction of this force?
- What is the significance of the Reynolds number mentioned in the technical notes? What does a "drag crisis" near a Reynolds number of 10^5 imply for the simulation's accuracy?
- According to Timmerman and van der Weele, why is it somewhat surprising that the buoyant force is often ignored in the literature on sports ballistics?
- Explain the difference between how top spin and backspin affect the trajectory of a beach ball, based on the information provided (including the sample questions).
- What is the "spin factor," and how does it relate to the Magnus force acting on the beach ball?
Answer Key for Quiz
- The effects are more pronounced on a beach ball due to its relatively low mass compared to its size. This means that even small forces like drag, buoyancy, and the Magnus effect can produce noticeable changes in its motion.
- The "Show Velocity" checkbox displays vectors representing the ball's velocity and angular velocity, allowing users to visualize the ball's movement and rotation. The "Show Forces" checkbox displays vectors for all forces acting on the ball, such as gravity, drag, buoyancy, and the Magnus force, making the influence of each force apparent.
- To simulate a simple curve ball, users should set a non-zero spin (between 1 to 5 rotations per second is suggested) and orient the spin axis vertically. This is achieved by setting the tilt to ±90 degrees and the azimuth to 0.
- The measured mass remains the same because a balance measures the gravitational force on the ball (its weight). The air inside contributes to the overall inertia of the ball when it is thrown, but its weight is offset by the buoyant force due to the displaced volume of air.
- The drag force opposes the motion of the beach ball. It is modeled in the simulation by the equation F_drag = -½ ρ C_D A v^2 v̂, where ρ is the air density, C_D is the drag coefficient, A is the cross-sectional area, v is the velocity magnitude, and v̂ is the unit vector in the direction of velocity.
- The Magnus effect creates a force perpendicular to both the velocity and the rotation axis, causing the ball's trajectory to curve. The size of the effect depends on both the velocity and the angular velocity (spin rate) of the ball, and its direction is determined by the right-hand rule applied to the velocity and spin axis vectors.
- The Reynolds number helps predict the nature of the airflow around the ball and is important for determining the drag coefficient. A "drag crisis" near Re=10^5 indicates a region where the drag model becomes more complex and the simulation might not provide highly accurate results.
- Timmerman and van der Weele find it curious because the same medium (air) that is responsible for the drag force also introduces a buoyant force. They argue that both should be considered when analyzing the motion of objects through the air.
- Backspin creates an upward Magnus force, causing the ball to experience greater lift and potentially travel further. Top spin creates a downward Magnus force, causing the ball to dip and reach the ground faster.
- The spin factor (S) is a dimensionless parameter related to the ratio of the ball's rotational speed to its translational speed (S = rω/v). It influences the dimensionless spin parameter (C_spin) in Clanet's formulation of the Magnus force, thus affecting the magnitude of the Magnus force.
Essay Format Questions
- Discuss the relative importance of drag, buoyancy, and the Magnus effect on the trajectory of a beach ball. Under what conditions might one of these forces be dominant over the others?
- Compare and contrast the factors influencing the trajectory of a beach ball with those affecting a baseball or tennis ball. How do the physical properties of these balls (mass, size, surface) contribute to the differences in their flight?
- Explain how manipulating the spin (rate and axis orientation) of a beach ball can be used to achieve different trajectory effects, such as curve balls, floaters, and sinkers. Use the simulation controls described in the text to illustrate your points.
- Critically evaluate the statement: "While the beach ball simulation model incorporates several complexities beyond simple projectile motion, it still has limitations in accurately predicting real-world trajectories under all conditions." Support your answer with evidence from the technical notes.
- Design an experiment (either physical or using the provided simulation) to investigate the relationship between the spin rate of a beach ball and the horizontal distance it travels. Identify the independent and dependent variables, and discuss potential sources of error.
Glossary of Key Terms
- Aerodynamics: The study of motion through the air and the forces exerted by air on moving objects.
- Azimuthal Angle: The angle in the horizontal plane, used to define the orientation of the spin axis.
- Ballistics: The study of the motion of projectiles.
- Buoyancy: The upward force exerted by a fluid that opposes the weight of an immersed object.
- Drag Coefficient (C_D): A dimensionless number that quantifies the resistance of an object in a fluid environment.
- Drag Crisis: A sudden drop in the drag coefficient of a smooth sphere at a critical Reynolds number.
- Drag Force: The force exerted by a fluid that opposes the motion of an object through it.
- Inertia: The resistance of any physical object to any change in its velocity.
- Magnus Effect: The force on a spinning object in a fluid that acts perpendicular to the direction of flow and the axis of spin.
- Projectile Motion: The motion of an object thrown or projected into the air, subject only to acceleration due to gravity (in a simplified model).
- Reynolds Number (Re): A dimensionless quantity that is used to help predict similar flow patterns in different fluid flow situations by considering the ratio of inertial forces to viscous forces.
- Spin Factor (S): A dimensionless parameter representing the ratio of the tangential speed due to spin to the translational speed of a rotating object.
- Tilt: The angle of the spin axis relative to the horizontal plane.
- Trajectory: The path followed by a projectile moving under the action of given forces.
- Velocity: A vector quantity that specifies both the speed and direction of motion.
- Weight: The force exerted on an object due to gravity.
Sample Learning Goals
[text]
For Teachers
[text]
Research
[text]
Video
Backspin Basketball Flies Off Dam by Veritasium
Physics of toys- Cup Flyers // Homemade Science with Bruce Yeany by Bruce Yeany
Version
https://weelookang.blogspot.com/2020/03/beach-ball-physics-for-sports.html

Question 1: A student claims that having a backspin on the ball increases the distance travelled by the ball as compared to having a top spin. True or false?
True. Backspin causes the ball to travel further than with having a top spin.
Question 2: Taking the default point of reference from the sim (blue arrow points up, red arrow points towards user, and green arrow towards right of user), how does having a left spin affect the trajectory of the ball?
Ball moves to the right and also away from the user.
Question 3: If a tennis player hit the ball with a certain spin and it reached the ground faster than expected, what type of spin did the ball experience? (assuming the tennis ball in this case is modelled by the same ball in the sim)
Top spin. This exerts a downward force on the ball and thus makes it hit the ground faster.
Other Resources
[text]
Frequently Asked Questions: Beach Ball Physics Simulation
1. What makes the physics of a thrown beach ball particularly interesting compared to other sports balls like baseball or soccer balls?
The relatively low mass of a beach ball in comparison to its size exaggerates subtle effects that are also present in the motion of other sports balls. This makes phenomena like drag, buoyancy, and the Magnus effect more pronounced and easier to observe and study.
2. This simulation allows the exploration of "complications" to simple projectile motion. What are these complications and how do they affect the trajectory of a beach ball?
The simulation models three main complications: * Drag: This is the air resistance that opposes the motion of the ball, causing it to slow down during its flight and reducing its range. * Buoyancy: This is the upward force exerted by the air displaced by the ball. While often ignored for denser sports balls, it plays a more significant role for the lightweight beach ball, effectively making it "float" more. * Magnus Effect: This is a force that causes the ball's trajectory to curve due to its spin. The direction of the curve depends on the direction of the spin axis and the ball's velocity.
3. How can users interact with the simulation to observe these effects?
Users can control various parameters through the simulation interface, including: * Launch parameters: Initial height, launch speed, and launch angle. * Ball properties: Radius and mass, allowing for the exploration of different beach ball sizes. * Spin: Rotations per second, tilt, and azimuthal angle of the spin axis, enabling the investigation of different spin types and their effects on the trajectory. * Aerodynamic parameters: Allowing advanced users to adjust factors influencing drag and lift. * Visualization: Options to show velocity vectors, angular velocity vectors, and the forces acting on the ball (gravity, buoyancy, drag, and Magnus force). Graphs can also be displayed for ancillary information like Reynolds number and spin factor.
4. Why is the buoyant force often ignored in the physics of other sports balls but considered important for beach balls in this simulation?
For denser sports balls like baseball, soccer balls, and volleyballs, the buoyant force (the weight of the air displaced by the ball) is very small compared to the ball's weight and inertia. However, because a beach ball has a much lower mass relative to its volume, the buoyant force becomes a more significant fraction of the total forces acting on it and thus has a more noticeable impact on its motion.
5. How does spin affect the trajectory of a beach ball, and what are some examples of spin and their resulting effects?
Spin imparts a force perpendicular to both the velocity and the spin axis, known as the Magnus force, causing the ball to curve. Examples include: * Curve ball: Achieved with spin about a vertical axis (tilt ±90 degrees, azimuth 0), causing the ball to curve sideways. * Floating effect (backspin): Achieved with spin directed backward (tilt 0, azimuth -90 degrees), creating an upward Magnus force that opposes gravity and can make the ball travel further. * Top spin (sinker): Achieved with spin directed forward (tilt 0, azimuth +90 degrees), creating a downward Magnus force that causes the ball to drop more quickly.
6. What are the key forces that the simulation takes into account when modeling the beach ball's motion?
The complete model dynamics include the following forces: * Gravity: The downward force due to the Earth's gravitational pull. * Buoyancy: The upward force exerted by the displaced air. * Drag Force: The air resistance opposing the ball's motion. * Magnus Force: The force resulting from the ball's spin and its movement through the air, causing the trajectory to curve.
7. The technical notes mention the "drag crises" near a Reynolds number of 10^5. What is the significance of this and why should users be aware of this limitation?
The drag coefficient, which influences the drag force, can change abruptly at certain Reynolds numbers (a dimensionless quantity indicating the ratio of inertial forces to viscous forces within a fluid). The "drag crisis" around Re = 10^5 signifies a significant drop in the drag coefficient for smooth spheres. The models used in the simulation, while sophisticated, may not perfectly capture these complex aerodynamic phenomena across all launch conditions. Therefore, users should be aware that the simulation's accuracy might be limited, especially when the ball's flight parameters lead to Reynolds numbers near this critical value.
8. How does the simulation account for the mass of the air inside the beach ball?
The simulation notes that when weighing a beach ball on a balance, the mass measured is the same whether the ball is inflated or empty. This is because the buoyant force offsets the weight of the air inside. However, when considering the ball's inertia (its resistance to changes in motion), the mass of the air inside the inflated ball does contribute. The simulation allows users to input the mass as measured on a balance, acknowledging that the internal air contributes to the overall inertia even though its weight is countered by buoyancy.
- Details
- Written by Jonathan
- Parent Category: Physical & Sports Education
- Category: Physical Education
- Hits: 6490