About
Using The Beach Ball Physics Model
 The physics of a thrown beach ball can be very interesting. Because of
its relatively low mass (compared to its size), subtle effects that are
important in sports like baseball, soccer and volleyball become
exaggerated in the beach ball’s motion. This simulation allows users to
explore a simple model of several “complications” to simple projectile
motion: drag, buoyancy and the Magnus effect. Drag slows the ball down,
buoyancy makes the ball “float” and the Magnus effect puts a curve on
the ball’s trajectory.
The physics of a thrown beach ball can be very interesting. Because of
its relatively low mass (compared to its size), subtle effects that are
important in sports like baseball, soccer and volleyball become
exaggerated in the beach ball’s motion. This simulation allows users to
explore a simple model of several “complications” to simple projectile
motion: drag, buoyancy and the Magnus effect. Drag slows the ball down,
buoyancy makes the ball “float” and the Magnus effect puts a curve on
the ball’s trajectory.
Simulation Controls:
The simulations main display includes an interactive 3-D display of the ball in flight. The “Show Velocity” checkbox will add a pair of vectors for the ball’s velocity and angular velocity (both scaled to the ball’s launch speed). The “Show Forces” checkbox adds vectors for all the forces contributing to the ball’s dynamics. A pair of graphs may be hidden or viewed for ancillary information using the Show Graphs checkbox.
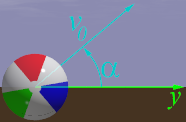 The basic ball launch parameters are the initial height of the ball, the
launch speed and the launch angle α (from horizontal).
The basic ball launch parameters are the initial height of the ball, the
launch speed and the launch angle α (from horizontal).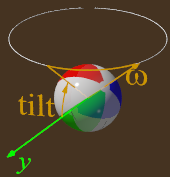
Beach Balls come in various sizes, so the radius and mass of the ball can be specified. Note that the assumption is that the mass given is what would be measured on a balance; the mass of the air inside the ball does not affect such measurements as its weight is offset by the buoyancy due to the displaced volume of air. To see the buoyant force in a simple way, note that if you weigh your beach ball empty or inflated, you will get the same measurement and yet the inflated ball’s contents do contribute to the overall inertia.
The simulation also allows the adjustment of some of the aerodynamic parameters. See the technical notes for discussion. For those interested in the aerodynamics, the Reynolds number and Spin factor are also displayed.
The Physics of Beach Ball Trajectories: Technical Notes
The model employed in this simulation follows Clanet’s “Sports Ballistics”.1 This simulation takes up as the positive z direction and the initial velocity of the ball to be in the y-z plane.
Gravity and Buoyancy
In a Physics Teacher paper on the vertical motion accounting for aerodynamic effects, Timmerman and van der Weele2 note
The mass (and hence the weight) of a beach ball are easy to determine: just place it on an electronic balance. The same results will be obtained whether the ball is inflated or not. When a ball is thrown, the air inside goes for a ride as well, and in the case of a beach ball, this is a significant contribution to inertia:
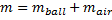
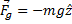
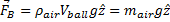
Drag Force
Drag force, or air resistance is the friction effect of moving though the air. It will be a significant force for almost any toss of the beach ball. The drag force is opposes motion and it is modeled in this simulation by
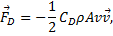 ,
,

Magnus Effect
The Magnus force is very noticeable when it is used to make the trajectory of a ball curve while in flight. The size of the effect depends upon both the velocity and angular velocity of the ball, and the direction is always perpendicular to both the velocity and the rotation axis of the ball’s spin. The force is often referred to as lift, and (following Clanet) is given by:
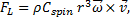
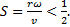
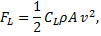
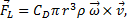
Complete Model Dynamics
The full beach ball dynamics used in the model is given by
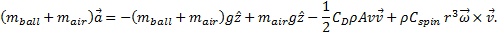
(1) Sports Ballistics by Clanet, Christophe, Annual Review of Fluid Mechanics, 01/2015, Volume 47, Issue 1
(2) On the rise and fall of a ball with linear or quadratic drag by Timmerman, Peter; Weele, van der, Jacobus P, American Journal of Physics, 1999, Volume 67, Issue 6
(3) For more information on drag, see https://en.wikipedia.org/wiki/Drag_coefficient
(4) Nathan AM. 2008. The effect of spin on the flight of a baseball. Am. J. Phys. 76:119–24
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits

 Michael R. Gallis, Ryan Vidal; lookang
Michael R. Gallis, Ryan Vidal; lookang
Overview:
These sources focus on the physics governing the trajectory of a beach ball, particularly in the context of sports. Due to the beach ball's unique characteristics – low mass relative to its size – certain aerodynamic effects that are often subtle in other sports become significantly exaggerated and thus easier to study. The primary source is an interactive JavaScript simulation that models these complexities, accompanied by technical notes explaining the underlying physics.
Main Themes and Important Ideas/Facts:
1. Exaggerated Aerodynamic Effects:
- The core idea is that a beach ball's motion vividly demonstrates aerodynamic forces crucial in many sports. The simulation intro states: "Because of its relatively low mass (compared to its size), subtle effects that are important in sports like baseball, soccer and volleyball become exaggerated in the beach ball’s motion."
2. Key Forces Influencing Trajectory (Modeled in the Simulation):
- Drag: Air resistance that opposes the motion of the ball, causing it to slow down. The technical notes state: "Drag force, or air resistance is the friction effect of moving though the air. It will be a significant force for almost any toss of the beach ball." The simulation allows adjustment of aerodynamic parameters and displays the Reynolds number, relevant to drag. Experimental data suggests a drag coefficient closer to 0.5 for a beach ball, higher than typical values for denser sports balls (around 0.25).
- Buoyancy: The upward force exerted by the air displaced by the ball, making it "float." The technical notes highlight that buoyancy is often ignored in sports ballistics literature, despite air being the medium responsible for drag: "… we include the buoyant force, which is almost always forgotten or ignored in the literature on this topic. This is somewhat curious, since the medium that is responsible for the drag force at the same time introduces a buoyant force." While negligible for denser sports balls, buoyancy is more significant for lighter beach balls. The simulation considers the inertia of the air inside the ball, noting that while it doesn't affect balance measurements, it contributes to the overall inertia.
- Magnus Effect: The force that causes a spinning ball to curve in flight. The technical notes explain: "The Magnus force is very noticeable when it is used to make the trajectory of a ball curve while in flight. The size of the effect depends upon both the velocity and angular velocity of the ball, and the direction is always perpendicular to both the velocity and the rotation axis of the ball’s spin." The simulation allows users to control the spin rate and the orientation of the spin axis to observe different curve ball, floating (backspin), and sinking (topspin) effects. Typical spin rates of 1 to 5 rotations per second are mentioned for curve balls.
3. Simulation Features and Controls:
- The simulation provides an interactive 3D display of the ball's flight.
- Users can toggle the display of velocity vectors (linear and angular) and force vectors (drag, buoyancy, Magnus, gravity).
- Graphs for ancillary information can be viewed.
- Adjustable launch parameters include initial height, launch speed, and launch angle.
- Spin can be controlled by rotations per second, tilt (up/down), and azimuthal angle (horizontal rotation) of the spin axis. Setting spin to 0 disables the Magnus effect. Specific spin settings are provided to demonstrate curve balls, backspin "floating," and topspin "sinking."
- The ball's radius and mass can be specified.
- Aerodynamic parameters can be adjusted (refer to technical notes for details).
- The Reynolds number and Spin factor are displayed for those interested in aerodynamics.
4. Underlying Physics Model:
- The simulation's model is based on Clanet’s "Sports Ballistics."
- It considers gravity acting in the negative z-direction and the initial velocity in the y-z plane.
- Mathematical formulations for drag force (\(\vec{F}_D = -\frac{1}{2} \rho A C_D |\vec{v}| \vec{v}\)) and Magnus force (\(\vec{F}L = \frac{1}{2} \rho A r C{spin} \vec{\omega} \times \vec{v}\) or the alternative formulation using lift coefficient \(C_L\)) are presented.
- The complete model dynamics are represented by a vector sum of forces divided by mass: \(\frac{d\vec{v}}{dt} = \frac{\vec{F}_g + \vec{F}_B + \vec{F}D + \vec{F}L}{m{total}}\), where \(m{total}\) includes the mass of the ball material and the air inside.
5. Limitations of the Model:
- The technical notes include a crucial caveat: "Bottom line: as sophisticated as this model is compared to drag-free ballistic motion, one should still not necessarily expect high fidelity results over all launch conditions." This is particularly relevant at the "drag crises" near a Reynolds number of \(10^5\), where drag and lift models become more complex.
6. Sample Learning from the Simulation (FAQ):
- Backspin vs. Topspin: Backspin increases the distance travelled compared to topspin (True).
- Left Spin Effect: With the default orientation, a left spin causes the ball to move to the right and away from the user.
- Faster Ground Contact: A ball experiencing topspin will reach the ground faster due to the downward force it generates.
Quotes:
- "Because of its relatively low mass (compared to its size), subtle effects that are important in sports like baseball, soccer and volleyball become exaggerated in the beach ball’s motion." (About section)
- "Drag slows the ball down, buoyancy makes the ball ‘float’ and the Magnus effect puts a curve on the ball’s trajectory." (About section)
- "… we include the buoyant force, which is almost always forgotten or ignored in the literature on this topic. This is somewhat curious, since the medium that is responsible for the drag force at the same time introduces a buoyant force." (Technical Notes - Gravity and Buoyancy)
- "The Magnus force is very noticeable when it is used to make the trajectory of a ball curve while in flight." (Technical Notes - Magnus Effect)
- "Bottom line: as sophisticated as this model is compared to drag-free ballistic motion, one should still not necessarily expect high fidelity results over all launch conditions." (Technical Notes - Complete Model Dynamics)
Potential Applications:
- Educational tool for physics, physical education, and sports science, demonstrating aerodynamic principles.
- Allows for qualitative and quantitative exploration of factors affecting projectile motion with significant air resistance and spin.
- Provides insights into the flight dynamics of various sports balls by highlighting the exaggerated effects on a beach ball.
This briefing document summarizes the key aspects of the provided sources, focusing on the physics of beach ball trajectories and the features of the associated JavaScript simulation.
Beach Ball Physics Study Guide
Key Concepts:
- Projectile Motion: The motion of an object projected into the air, influenced by gravity.
- Drag Force: The resistive force experienced by an object moving through a fluid (like air), opposing its motion.
- Buoyant Force: The upward force exerted by a fluid that opposes the weight of an immersed object.
- Magnus Effect: The force acting on a rotating object moving through a fluid, perpendicular to both the velocity and the axis of rotation, causing a curved trajectory.
- Spin Rate: The frequency of rotation of an object, typically measured in rotations per second (rps).
- Spin Axis Orientation: The direction of the axis around which an object rotates, defined by tilt and azimuthal angles.
- Drag Coefficient: A dimensionless quantity that quantifies the drag or resistance of an object in a fluid environment.
- Reynolds Number: A dimensionless quantity that describes the ratio of inertial forces to viscous forces within a fluid which is subjected to relative internal movement due to different fluid velocities.
- Spin Factor: A dimensionless parameter that relates the surface speed due to rotation to the translational speed of a spinning object, influencing the Magnus force.
- Inertia: The resistance of an object to changes in its state of motion.
- Terminal Velocity: The constant speed that a freely falling object eventually reaches when the drag force equals the gravitational force.
- Lift Coefficient: A dimensionless coefficient that relates the lift generated by a body to the fluid density around the body, the fluid velocity, and a reference area.
Quiz:
- Explain why the effects of drag, buoyancy, and the Magnus effect are more noticeable on a beach ball compared to a baseball.
- Describe how the "Show Velocity" and "Show Forces" checkboxes in the simulation can help users understand the physics of a beach ball's flight.
- How does backspin on a beach ball typically affect its vertical trajectory compared to a ball with no spin, considering the Magnus effect?
- If a beach ball is thrown with a vertical spin axis, what kind of trajectory would you expect to see, and what is this effect called?
- Why does the simulation note that the mass measured on a balance for a beach ball is the same whether it's inflated or deflated?
- According to the technical notes, what is the primary reason buoyancy is often overlooked in the literature on sports ballistics?
- How does the drag force modeled in the simulation affect the velocity of the beach ball during its flight?
- In the context of the Magnus effect, what is the relationship between the direction of the force, the velocity of the ball, and the axis of its spin?
- The technical notes mention a "drag crisis" at a certain Reynolds number. What does this suggest about the accuracy of the drag model across all launch conditions?
- What are the typical values for the drag coefficient of a soccer ball and a beach ball, as mentioned in the technical notes?
Answer Key:
- Beach balls have a relatively low mass compared to their large size. This low inertia makes them more susceptible to the influence of smaller forces like drag, buoyancy, and the Magnus effect, causing these effects to be more pronounced in their motion compared to denser, smaller balls like baseballs.
- The "Show Velocity" checkbox displays vectors for the ball's velocity and angular velocity, allowing users to visualize the direction and magnitude of these quantities throughout the flight. The "Show Forces" checkbox displays vectors for all forces acting on the ball (gravity, drag, buoyancy, Magnus), helping users understand which forces are influencing the ball's motion at any given time.
- Backspin typically creates an upward Magnus force on the beach ball, opposing gravity to some extent. This can result in the ball staying in the air longer and potentially traveling a greater horizontal distance compared to a ball with no spin or topspin.
- A beach ball thrown with a vertical spin axis will typically exhibit a curved trajectory in the horizontal plane. This sideways deviation is due to the Magnus effect, where the spinning motion interacting with the airflow creates a lateral force, often referred to as a curveball effect.
- The mass measured on a balance reflects the total mass of the beach ball, including the material of the ball itself. The weight of the air inside the inflated ball is offset by the buoyant force due to the volume of air it displaces, resulting in the same balance reading whether the ball is inflated or not.
- The technical notes suggest that buoyancy is often overlooked because for most balls used in sports (baseball, soccer, volleyball, etc.), the buoyant force and the inertia of the air contained within the ball are typically negligible compared to other forces like gravity and drag.
- The drag force, as modeled in the simulation, acts in the opposite direction to the ball's velocity. It constantly opposes the motion of the beach ball, causing it to decelerate and reducing its speed over time during its flight.
- The Magnus force is always perpendicular to both the velocity vector of the ball and the vector representing its angular velocity (spin axis). The direction of the force depends on the direction of the spin and the velocity of the air relative to the ball.
- The mention of a "drag crisis" near a Reynolds number of 10^5 indicates that the models used for drag and lift can become less accurate under certain high-speed conditions. Therefore, the simulation might not produce highly accurate results for all possible launch parameters.
- The technical notes cite a typical drag coefficient of about 0.25 for soccer, volleyball, and basketball, while local experiments suggest a typical drag coefficient closer to 0.5 for a beach ball.
Essay Format Questions:
- Discuss the relative importance of drag, buoyancy, and the Magnus effect in determining the trajectory of a thrown beach ball. Provide specific examples of how each force can influence its motion, referencing the simulation controls and technical notes.
- Explain how manipulating the spin rate and spin axis orientation in the simulation can create different types of curved trajectories for a beach ball. Describe the physics behind these curves, relating them to the Magnus effect and its dependence on these parameters.
- Critically evaluate the statement: "While a beach ball might seem like a simple object, its flight path involves complex physics that are often simplified or ignored for other sports balls." Support your argument with evidence from the provided sources.
- Considering the technical notes' discussion of the drag force and the Magnus effect models, what are some limitations or caveats to keep in mind when using the beach ball physics simulation to predict real-world trajectories?
- Compare and contrast the factors that influence the trajectory of a beach ball with those that influence the trajectory of another sports ball (e.g., a baseball or soccer ball), highlighting the role of air resistance and spin in each case.
Sample Learning Goals
[text]
For Teachers
[text]
Research
[text]
Video
Backspin Basketball Flies Off Dam by Veritasium
Physics of toys- Cup Flyers // Homemade Science with Bruce Yeany by Bruce Yeany
Version
https://weelookang.blogspot.com/2020/03/beach-ball-physics-for-sports.html

Question 1: A student claims that having a backspin on the ball increases the distance travelled by the ball as compared to having a top spin. True or false?
True. Backspin causes the ball to travel further than with having a top spin.
Question 2: Taking the default point of reference from the sim (blue arrow points up, red arrow points towards user, and green arrow towards right of user), how does having a left spin affect the trajectory of the ball?
Ball moves to the right and also away from the user.
Question 3: If a tennis player hit the ball with a certain spin and it reached the ground faster than expected, what type of spin did the ball experience? (assuming the tennis ball in this case is modelled by the same ball in the sim)
Top spin. This exerts a downward force on the ball and thus makes it hit the ground faster.
Other Resources
[text]
Frequently Asked Questions: Beach Ball Physics
1. Why is the physics of a beach ball's trajectory particularly interesting compared to other sports balls?
Due to its relatively low mass compared to its size, a beach ball exaggerates subtle aerodynamic effects that are also present in sports like baseball, soccer, and volleyball. This makes phenomena like drag, buoyancy, and the Magnus effect more noticeable and easier to study.
2. What are the main forces that significantly influence the flight of a thrown beach ball?
The primary forces influencing a beach ball's trajectory are: * Gravity: The downward force due to the ball's mass. * Drag: Air resistance that opposes the motion of the ball, slowing it down. The drag coefficient for a beach ball is typically higher than for denser sports balls. * Buoyancy: An upward force exerted by the displaced air. While often ignored for denser sports balls, it's a more significant factor for light beach balls. * Magnus Effect: A sideways force produced by the spin of the ball, causing its trajectory to curve.
3. How does buoyancy affect a beach ball's motion, and why is it often overlooked in the physics of other sports balls?
Buoyancy is the upward force equal to the weight of the air displaced by the beach ball. It acts to counteract gravity, making the ball "float" more than a denser object. This force is often ignored for sports balls like baseballs or soccer balls because their mass is significantly greater relative to the air they displace, making the buoyant force negligible in comparison. However, for a light and large beach ball, buoyancy plays a more significant role in its overall dynamics.
4. What is the Magnus effect, and how can a beach ball's spin be manipulated to create different flight paths?
The Magnus effect is a force acting on a spinning object moving through a fluid (like air). This force is perpendicular to both the velocity of the ball and its axis of rotation, causing the ball's trajectory to curve. * Backspin: Creates an upward Magnus force, causing the ball to stay in the air longer and travel further. * Topspin: Creates a downward Magnus force, causing the ball to dip and reach the ground faster. * Sidespin: Creates a sideways Magnus force, causing the ball to curve left or right in its flight path. The simulation allows users to control the spin rate, tilt, and azimuthal angle of the spin axis to explore these different effects.
5. The sources mention a simulation that allows users to adjust various parameters. What are some of the key parameters that can be controlled and observed in this simulation?
The simulation allows users to manipulate and observe the effects of: * Launch parameters: Initial height, launch speed, and launch angle. * Ball properties: Radius and mass. * Spin properties: Spin rate (rotations per second), tilt of the spin axis (up or down), and azimuthal angle of the spin axis (rotation about a vertical axis). * Aerodynamic parameters: Although not explicitly detailed for adjustment in the excerpts, the simulation models drag with a drag coefficient, which implicitly accounts for some aerodynamic properties. * Visualizations: Velocity and angular velocity vectors, force vectors (gravity, drag, buoyancy, Magnus), and ancillary graphs. * Calculated values: Reynolds number and Spin factor, which are relevant for understanding the aerodynamic regime.
6. Why does the simulation include the "inertia of the air contained within the ball" in its model, even though it doesn't affect the measured weight on a balance?
While the air inside the beach ball has a buoyant force that offsets its weight when measured on a balance, this internal air still contributes to the overall inertia of the ball. Inertia is the resistance of an object to changes in its motion. When the ball is thrown and accelerated, the air inside must also be accelerated along with the outer material of the ball. Therefore, to accurately model the ball's response to forces, the simulation accounts for the inertia of the enclosed air.
7. The "Technical Notes" mention that the drag and lift models can become more complex at high Reynolds numbers. What does this imply about the accuracy of the simulation under all launch conditions?
The mention of "drag crises" near a Reynolds number of 10^5 indicates that the simplified models used for drag and the Magnus effect (lift) in the simulation may not accurately represent the real-world behavior of a beach ball under all conditions, particularly at very high speeds where turbulent airflow becomes dominant. Therefore, while the simulation provides a sophisticated model compared to simple projectile motion, users should be aware that its fidelity might decrease under extreme launch conditions that result in very high Reynolds numbers.
8. Based on the provided "Question 1" and "Question 3" examples related to the simulation, what are some practical insights one can gain about manipulating a ball's trajectory with spin in sports?
The examples suggest that: * Backspin can increase the range of a projectile: Question 1 states that backspin increases the distance traveled. This is because the upward Magnus force created by backspin counteracts gravity to some extent, allowing the ball to stay airborne longer. * Topspin can cause a ball to drop more quickly: Question 3 indicates that a ball with topspin will reach the ground faster. This is due to the downward Magnus force created by topspin, which adds to the effect of gravity.
These insights are relevant to various sports where spin is used strategically to control the trajectory of a ball, such as tennis, volleyball, and golf.
- Details
- Written by Jonathan
- Parent Category: Physical & Sports Education
- Category: Physical Education
- Hits: 6245


.png
)






.png)
 Michael R. Gallis, Ryan Vidal; lookang
Michael R. Gallis, Ryan Vidal; lookang