About

 

Translations

Code	Language		Translator	Run

Credits

Lam Meng Hwee

1. Introduction:

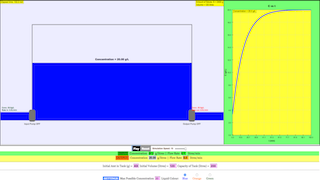
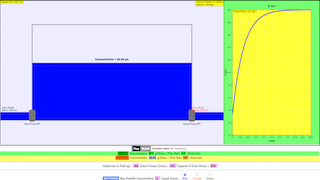
This briefing document reviews two provided sources, both titled "First Order DE (Concentration Changes in Tank)" and attributed to Lam Meng Hwee. The first source appears to be the theoretical basis, likely containing explanations and mathematical derivations. The second source is a webpage hosted by Open Educational Resources / Open Source Physics @ Singapore, featuring an embedded JavaScript HTML5 applet simulating the concentration changes in a tank. The analysis will focus on the main themes, important ideas, and potential pedagogical applications of these resources.

2. Source 1: Excerpts from "First Order DE (Concentration Changes in Tank)"

Due to the nature of the provided excerpt (only the title, author, and copyright information are present), it is impossible to detail the specific content, main themes, or important ideas within this source. However, based on the title, we can infer the likely subject matter.

Inferred Content: This document likely covers the mathematical modeling of how the concentration of a substance in a well-mixed tank changes over time. This typically involves setting up and solving a first-order linear differential equation. Key concepts likely discussed include:

• Rate of change of concentration: How the concentration increases or decreases depending on the inflow and outflow of solutions with different concentrations.
• Influx and efflux rates: The volume of solution entering and leaving the tank per unit time.
• Concentration of inflow: The concentration of the substance being added to the tank.
• Volume of the tank: The total volume of the solution in the tank, which may be constant or variable.
• Setting up the differential equation: Translating the physical scenario into a mathematical equation involving the derivative of the concentration with respect to time.
• Solving the differential equation: Using appropriate techniques (e.g., integrating factors) to find an expression for the concentration as a function of time.
• Initial conditions: The concentration of the substance in the tank at the beginning of the process, which is necessary to find a particular solution to the differential equation.
• Equilibrium concentration (steady state): The concentration that the solution in the tank approaches as time goes to infinity.

Without the actual content, we cannot provide direct quotes or specific details from this source. However, it serves as the theoretical foundation for the simulation model described in the second source.

3. Source 2: Excerpts from "Tank 2 Concentration JavaScript HTML5 Applet Simulation Model by Lam MH - Open Educational Resources / Open Source Physics @ Singapore"

This source provides context and access to an interactive simulation related to the topic of concentration changes in a tank.

Main Themes and Important Ideas:

• Interactive Learning: The core of this source is an embedded JavaScript HTML5 applet, emphasizing an interactive and visual approach to understanding the abstract concepts of differential equations and their applications. The "Embed this model in a webpage" functionality highlights its intended use in online educational materials.
• Open Educational Resources: The hosting of this model on "Open Educational Resources / Open Source Physics @ Singapore" signifies its commitment to freely available educational tools. The mention of a Creative Commons license in the "About" section of the model further reinforces this.
• Connection to First Order DE: The "About" section explicitly links the simulation model to the theoretical document "First Order DE (Concentration Changes in Tank)," indicating that the applet is designed to visually demonstrate the principles explained in that document.
• Practical Application of Mathematics: The simulation provides a concrete example of how first-order differential equations can be used to model real-world phenomena, specifically the mixing of solutions.
• Accessibility and Flexibility: Being an HTML5 applet, the simulation is likely accessible on various devices (desktops, tablets, smartphones) without the need for specific software installations.
• Community and Collaboration: The "Credits" section acknowledges Lam Meng Hwee as the author. The "Version" section, referencing improvements based on Joseph Chua's inputs, suggests a collaborative aspect in the development of the simulation.
• Broad Context of Open Source Physics: The webpage lists a vast array of other physics and mathematics simulations, demonstrating the breadth of resources available through the Open Source Physics @ Singapore project. These cover diverse topics ranging from mechanics and electromagnetism to chemistry and even educational games.

Key Facts and Information:

• Title of the Simulation: Tank 2 Concentration JavaScript HTML5 Applet Simulation Model by Lam MH.
• Author of the Underlying Theory and Simulation: Lam Meng Hwee.
• Platform: Open Educational Resources / Open Source Physics @ Singapore.
• Technology: JavaScript HTML5 Applet.
• License: Released under a license (likely Creative Commons based on the footer of the webpage, although the specific license for the simulation itself isn't explicitly stated in the excerpt).
• Embeddable: The model can be embedded into other webpages using an iframe.
• Related Theoretical Resource: "First Order DE (Concentration Changes in Tank)" by Lam Meng Hwee.
• Sample Learning Goals & For Teachers: These sections are mentioned but contain "[texthttps://iwant2study.org/lookangejss/00workshop/2017FelixPaco/day4/ejss_model_Tank/Tank_Simulation.xhtml " frameborder="0">" (This provides the code to embed the interactive simulation.)

4. Potential Pedagogical Applications:

The combination of the theoretical document and the interactive simulation offers significant pedagogical value for teaching and learning about first-order differential equations and their applications:

• Visualization of Abstract Concepts: The simulation can help students visualize how the concentration changes dynamically based on different parameters (inflow rate, outflow rate, inflow concentration, tank volume), making the abstract mathematical concepts more concrete.
• Interactive Exploration: Students can manipulate the parameters of the simulation and observe the resulting changes in concentration over time, fostering a deeper understanding through active learning.
• Connection between Theory and Practice: The simulation serves as a practical application of the theoretical concepts explained in the "First Order DE" document, helping students see the relevance of mathematics to real-world scenarios.
• Experimentation and Hypothesis Testing: Students can use the simulation to test hypotheses about how different factors affect the final concentration or the time it takes to reach a certain concentration.
• Differentiated Learning: The interactive nature of the simulation can cater to different learning styles, particularly visual and kinesthetic learners.
• Assessment and Feedback: While not explicitly stated, the simulation could potentially be used as a tool for formative assessment, allowing students to check their understanding of the concepts.

5. Conclusion:

The provided resources, particularly the "Tank 2 Concentration JavaScript HTML5 Applet Simulation Model," offer a valuable tool for educators and learners interested in understanding the application of first-order differential equations to model concentration changes in a tank. The simulation, built upon the theoretical foundation likely provided in the accompanying document, allows for interactive exploration and visualization of key concepts. The availability of these resources through an open educational platform promotes accessibility and collaborative learning. Further access to the full content of the "First Order DE (Concentration Changes in Tank)" document and exploration of the interactive simulation itself would provide a more comprehensive understanding of their educational potential. The extensive list of other simulations available on the Open Educational Resources / Open Source Physics @ Singapore website suggests a rich ecosystem of interactive learning tools developed by Lam Meng Hwee and others.

 

Study Guide: Tank Concentration Changes

Overview of Concepts

This study guide focuses on the principles of concentration changes in a tank, likely involving differential equations to model these changes over time. The materials provided include an applet simulation model and a resource titled "First Order DE (Concentration Changes in Tank)," suggesting that the core mathematical concept involves first-order differential equations. Key areas to understand include:

• Defining Concentration: Understanding how concentration is expressed (e.g., mass per unit volume).
• Flow Rates: Analyzing the rates at which solutions enter and leave the tank.
• Mixing: Considering the assumption of uniform mixing within the tank.
• Setting up Differential Equations: Translating the described physical process into a mathematical model using differential equations.
• Solving First-Order Differential Equations: Applying techniques to find the concentration as a function of time.
• Initial Conditions: Recognizing the importance of the starting concentration in determining the specific solution.
• Equilibrium/Steady-State Concentration: Understanding the long-term behavior of the concentration in the tank.
• Simulation Models: Recognizing how computational models can visualize and predict concentration changes under varying conditions.

Quiz

Answer the following questions in 2-3 sentences each.

1. What is the definition of concentration in the context of a solution in a tank? How is it typically expressed mathematically?
2. Explain the role of inflow rate and outflow rate in determining the change in the amount of solute within the tank over time.
3. What is the significance of the assumption of "uniform mixing" when modeling concentration changes in a tank?
4. Based on the title "First Order DE (Concentration Changes in Tank)," what type of mathematical equation is likely used to model this process? What does "first order" imply in this context?
5. What are initial conditions, and why are they necessary when solving a differential equation that models concentration change in a tank?
6. Describe what is meant by the equilibrium or steady-state concentration in a tank system with continuous inflow and outflow.
7. How can a JavaScript HTML5 applet simulation model, like the one mentioned, be helpful in understanding concentration changes in a tank?
8. Identify at least two variables that you might be able to manipulate within a simulation model of tank concentration changes. How would changing these variables likely affect the concentration over time?
9. Why is it important to consider the concentration of the incoming solution when analyzing concentration changes within the tank?
10. How might the volume of the solution in the tank change over time if the inflow rate and outflow rate are not equal? How would this volume change affect the concentration?

Quiz Answer Key

1. Concentration refers to the amount of solute present in a given volume of solution. Mathematically, it is typically expressed as mass of solute divided by volume of solution (e.g., kg/L) or moles of solute divided by volume of solution (molarity).
2. The inflow rate brings solute into the tank, increasing the total amount of solute, while the outflow rate removes the mixed solution, thus removing some solute and decreasing the total amount. The difference between the rates of solute entering and leaving determines the net change of solute in the tank.
3. The assumption of uniform mixing implies that the solute is instantaneously and evenly distributed throughout the entire volume of the solution in the tank. This allows us to assume that the concentration of the outflow is the same as the concentration within the tank at any given time.
4. A first-order differential equation is likely used. "First order" indicates that the equation involves the first derivative of the unknown function (in this case, likely the concentration or the amount of solute) with respect to the independent variable (time).
5. Initial conditions specify the state of the system at a particular starting time, usually time zero. For a tank problem, this typically means the concentration (or amount of solute) in the tank at the beginning of the process, which is crucial for finding a unique solution to the differential equation.
6. Equilibrium or steady-state concentration is the concentration that the solution in the tank approaches as time goes to infinity, assuming the inflow concentration and flow rates remain constant. At this point, the rate of solute entering the tank equals the rate of solute leaving.
7. A simulation model allows for the visualization of how concentration changes over time under different conditions without needing to solve the differential equation analytically. Users can often manipulate parameters like inflow rate, outflow rate, and inflow concentration to observe the resulting changes dynamically.
8. Two variables that could likely be manipulated are the inflow rate and the concentration of the inflow. Increasing the inflow rate of a solution with a higher concentration would likely cause the tank concentration to increase more rapidly towards that higher concentration.
9. The concentration of the incoming solution directly influences the amount of solute being added to the tank per unit time. A higher inflow concentration will introduce more solute, leading to a faster increase in the tank's concentration (or a higher equilibrium concentration).
10. If the inflow rate is greater than the outflow rate, the volume of the solution in the tank will increase over time. Conversely, if the outflow rate is greater, the volume will decrease. Changes in volume will directly affect the concentration because concentration is defined as the amount of solute per unit volume.

Essay Format Questions

1. Discuss the process of setting up a first-order differential equation to model the change in concentration of a solute in a well-mixed tank with constant inflow and outflow rates. Be sure to define all relevant variables and explain the physical meaning of each term in the equation.
2. Explain how the initial concentration of a solute in a tank and the concentration of the incoming solution influence the concentration of the solution in the tank over time. Consider scenarios where the inflow concentration is higher, lower, and equal to the initial concentration.
3. Describe the concept of steady-state concentration in a continuous flow tank system. Under what conditions is a steady state reached, and how can it be determined mathematically from the differential equation governing the system?
4. Analyze the benefits of using a simulation model, such as a JavaScript HTML5 applet, to study concentration changes in a tank compared to relying solely on analytical solutions of differential equations. What insights can a simulation provide that might be less apparent from the mathematical solution alone?
5. Consider a scenario where the volume of the solution in the tank is not constant due to unequal inflow and outflow rates. How would this variation in volume complicate the mathematical model for concentration changes, and what factors would need to be taken into account?

Glossary of Key Terms

• Solute: The substance that is dissolved in a solvent to form a solution (e.g., salt in water).
• Solvent: The substance in which the solute is dissolved (e.g., water).
• Solution: A homogeneous mixture of a solute dissolved in a solvent (e.g., saltwater).
• Concentration: The amount of solute present in a given amount of solution, often expressed as mass per unit volume or moles per unit volume.
• Inflow Rate: The volume of solution entering the tank per unit time.
• Outflow Rate: The volume of solution leaving the tank per unit time.
• Mixing: The process of dispersing the solute uniformly throughout the solvent in the tank.
• Differential Equation: A mathematical equation that relates a function with its derivatives.
• First-Order Differential Equation: A differential equation involving only the first derivative of the unknown function.
• Initial Condition: The value of the dependent variable (e.g., concentration) at a specific starting value of the independent variable (e.g., time).
• Equilibrium Concentration (Steady-State Concentration): The constant concentration that the system approaches after a sufficiently long time, when the rates of solute entering and leaving the tank are equal.
• Simulation Model: A computational representation of a real-world system that allows for experimentation and observation of its behavior under different conditions.

Sample Learning Goals

[text]

For Teachers

[text]

Research

[text]

Video

[text]

 Version:

1. http://weelookang.blogspot.sg/2016/02/vector-addition-b-c-model-with.html improved version with joseph chua's inputs
2. http://weelookang.blogspot.sg/2014/10/vector-addition-model.html original simulation by lookang

Other Resources

[text]