About

Simple Harmonic Motion

Guiding Questions

1. What are the characteristics of periodic motion? How can we study and describe such motion?
2. How can circular motion be related to simple harmonic motion (SHM)?
3. How do we analyse simple harmonic motion?

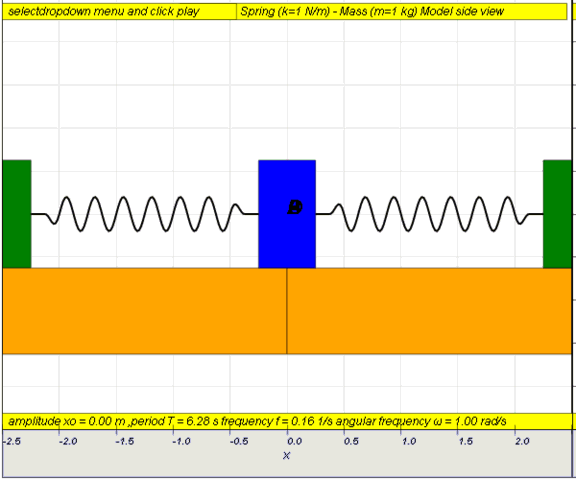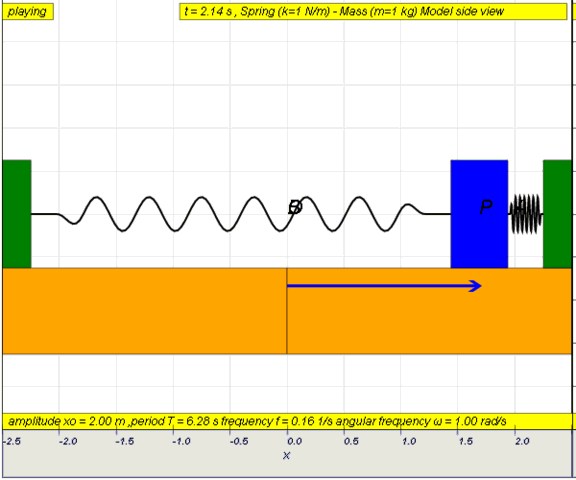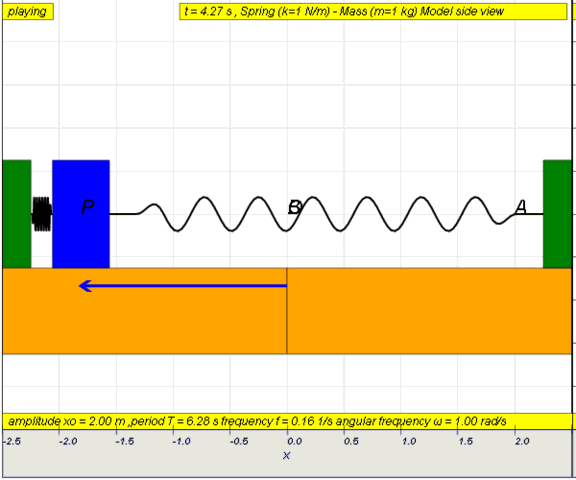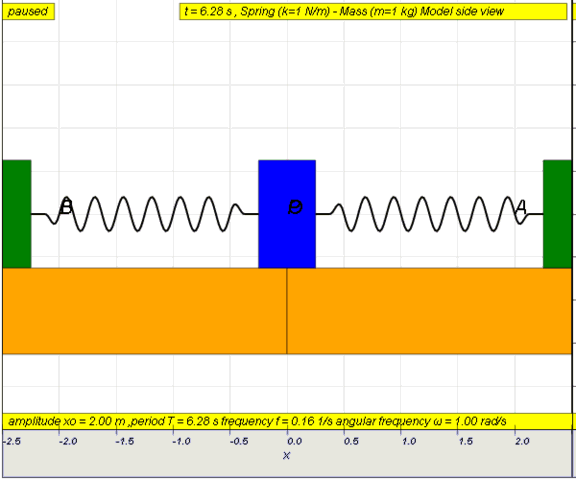
Learning Outcomes (LOs) 

1. describe simple examples of free oscillations.
2. investigate the motion of an oscillator using experimental and graphical methods.
3. understand and use the terms amplitude, period, frequency and angular frequency.
4. recognise and use the equation a =  - ω² x as the defining equation of simple harmonic motion.
5. recall and use x= x₀ ω sin( ωt )as a solution to the equation a =  - ω² x
6. recognise and use v = v₀ cos ( ω t )  , ${\displaystyle v=\pm \omega \sqrt{(x_0^2-x^2)}}$
7. describe with graphical illustrations, the changes in displacement, velocity and acceleration during simple harmonic motion.
8. describe the interchange between kinetic and potential energy during simple harmonic motion.
9. describe practical examples of damped oscillations with particular reference to the effects of the degree of damping and the importance of critical damping in cases such as a car suspension system.
10. describe practical examples of forced oscillations and resonance.
11. describe graphically how the amplitude of a forced oscillation changes with driving frequency near to the natural frequency of the system, and understand qualitatively the factors which determine the frequency response and sharpness of the resonance
12. show an appreciation that there are some circumstances in which resonance is useful and other circumstances in which resonance should be avoided.

Learning Experiences

1. Examine representations used in oscillations
   • Examine how different graphs are used to represent SHM. Draw links between the different graphs highlighting the positive and negative values and their interpretation. These will help students to understand SHM as a function of two variables (space and time) and understand the treatment of vector and scalar quantities .
2. Investigate factors affecting period of oscillations using experiments or a simulation
   • Design and carry out an experiment  to build a pendulum or spring-mass system to obtain a prescribed period. Present the experimental design, explaining the factors that determine the period of the oscillating system. This provides an opportunity for students to predict and collect data to ascertain the properties of a system and determine whether a motion is considered to be SHM. Students are also to understand that it is necessary for oscillations to be small for the motion to be considered as SHM. Students can also be shown other systems that demonstrate SHM . Simulations [1] [2] [3] ,  can also be used for students to investigate these factors.
3. Investigate phase using a turntable or a simulation
   • Investigate phase using a turntable  or a simulation  to associate each position in an SHM with a position on a uniform circular motion. This idea can be extended to the phase difference between different positions in an SHM. The association of SHM with uniform circular motion helps students to visualise many aspects of SHM. Students are to make mental links between three related ideas: physical position and velocity of the oscillator, angle in the associated uniform circular motion and the position of the oscillator on a displacement-time graph .
4. Build a model for SHM using a datalogger or simulation
   • Investigate the motion of a SHM system (pendulum, mass-spring system) using a datalogger  or a simulation . Students are to practice observing the motion and interpreting graphs before getting into the mathematical details of the equations. Compare the relationship between the different variables particularly note the values of these valuables at equilibrium position and at endpoints. Students should practice converting one graph into another.
5. Explore modelling of oscillation in molecules as SHM
   • Explore how oscillations of molecules bounded by the van der Waals interaction can be SHM if the amplitude is small [4] .
6. Explore benefits and danger of resonance
   • Explore various examples of resonance  and discuss the benefits  and dangers  of resonance.

1. Simple examples of free oscillations LO(a)

1.1 YouTube of many examples of oscillators

http://youtu.be/VKtEzKcg6_s This video can be used at the start of the first lecture (while students settle down for lecture) to introduce oscillations, to show various modes of oscillations and to interest them.

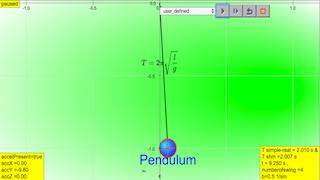
1.1.1 Example 1: Simple pendulum

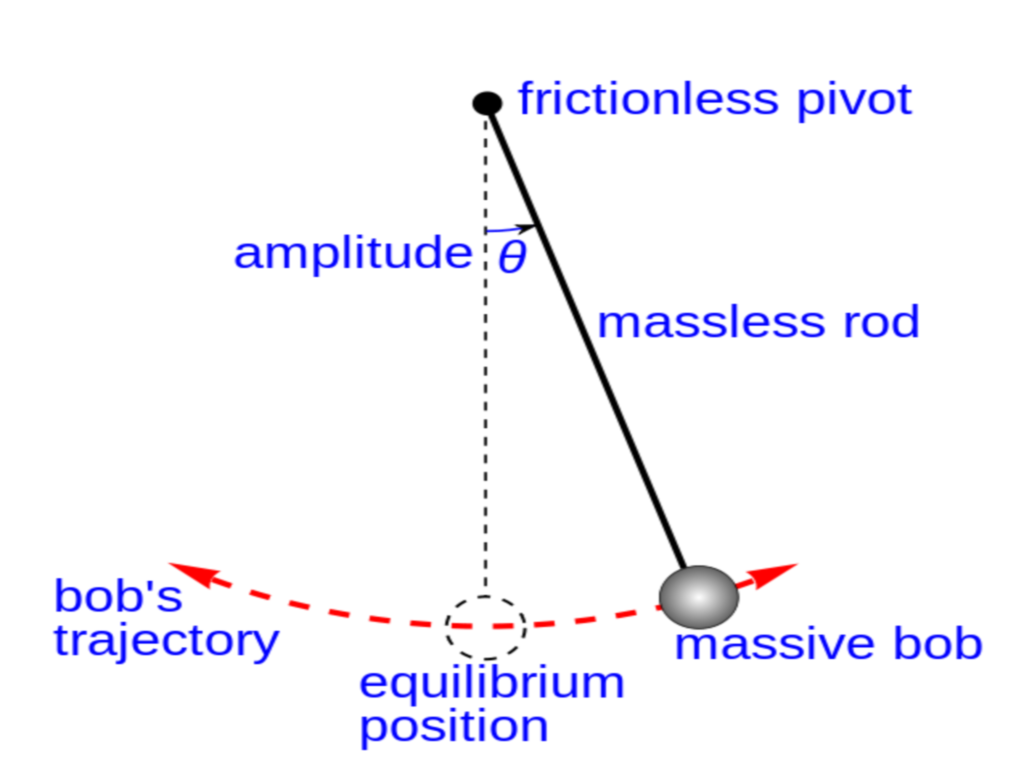
Static picture of a pendulum bob given an initial horizontal displacement and released to swing freely to produce to and fro motion

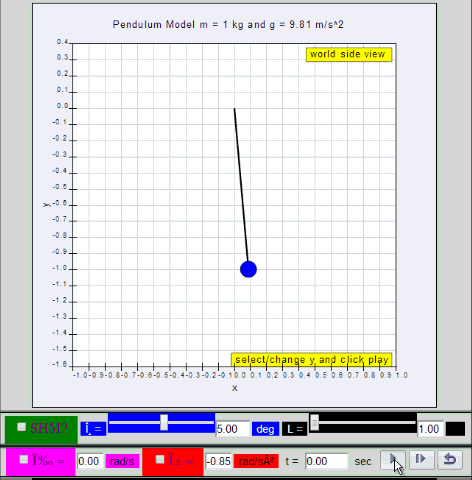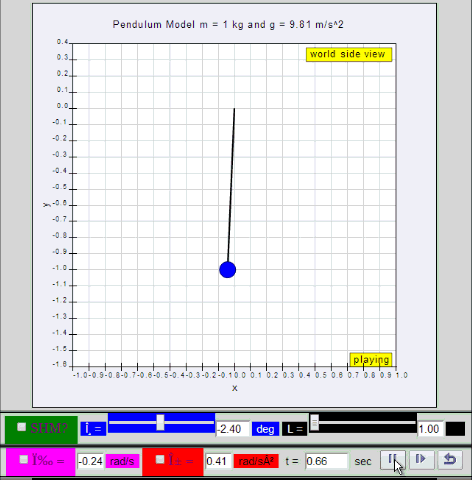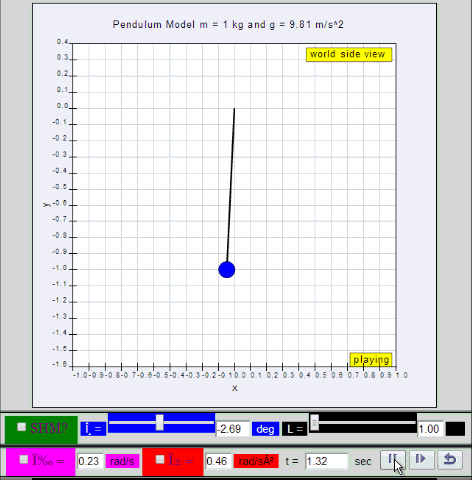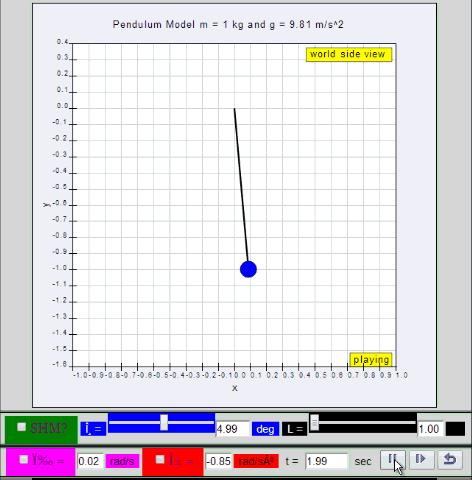
Dynamic picture of a pendulum bob given an initial horizontal displacement and released to swing freely to produce to and fro motion

1.1.2 Run Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/67

1.1.2.Q1: what is the maximum angle of release before the motion is not accurately described as a simple harmonic motion for the case of a simple free pendulum?

1.1.2.A1: : 10 degrees for error of , depending on what is the error acceptable, small angle is typically about less than 10 degree of swing from the vertical.

 

Translations

Code	Language		Translator	Run

Credits

weelookang@gmail.com; Fu-Kwun Hwang; Francisco Esquembre; Wolfgang Christian; Félix J. García

 

Pendulum Toy

• Source Type: Software tool compiled with EJS 6.1 BETA.
• Authorship and Licensing: Developed by a team including weelookang@gmail.com, Fu-Kwun Hwang, Francisco Esquembre, Wolfgang Christian, and Félix J. García. Released under a Creative Commons Attribution license (© 2021). This indicates the tool is likely freely available for use and adaptation with proper attribution.
• Main Theme: The title suggests this is a digital tool designed for users to interact with and explore the behavior of pendulums. The fact that it is "Compiled with EJS 6.1 BETA" points towards its likely use for creating simulations and visualizations of physical phenomena, possibly for educational purposes.
• Key Implications: The Creative Commons license makes this a valuable resource for educators looking for open-source tools to demonstrate pendulum motion. The mention of EJS (Easy JavaScript Simulations) suggests the tool is likely interactive and customizable.

2. Real Time Evolution Line Code 10 Pendulum JavaScript Model Simulation Applet HTML5

• Source Type: Interactive HTML5 simulation applet accessible online through "Open Educational Resources / Open Source Physics @ Singapore."
• Authorship: Developed within the context of the Open Educational Resources / Open Source Physics @ Singapore project. Real-time evolution code specifically mentions Shaun.
• Main Theme: This resource focuses on providing a real-time, interactive simulation of a pendulum, specifically highlighting its connection to Simple Harmonic Motion (SHM). The detailed "Learning Outcomes" and "Learning Experiences" sections clearly indicate its primary purpose is educational.
• Key Ideas and Facts:
• Simple Harmonic Motion (SHM): The resource explicitly links the pendulum's behavior (under small angle approximations) to SHM. This is evident in the section title "Simple Harmonic Motion" and the guiding questions like "How can circular motion be related to simple harmonic motion (SHM)?"
• Learning Outcomes (LOs): A comprehensive list of learning objectives is provided, covering fundamental aspects of oscillations and SHM. These include:
• Describing free oscillations.
• Investigating motion graphically and experimentally.
• Understanding and using terms like amplitude, period, frequency, and angular frequency.
• Recognizing and using the defining equation of SHM: "a = - ω2 x".
• Applying solution equations for displacement and velocity: "x= x0 ω sin( ωt )" and "v = v0 cos ( ω t ) , v = ± ω ( x 0 2 - x 2 )".
• Describing and illustrating changes in displacement, velocity, and acceleration graphically.
• Explaining the interchange between kinetic and potential energy.
• Discussing damped and forced oscillations, including resonance and its practical implications. The LO on resonance highlights its dual nature: "show an appreciation that there are some circumstances in which resonance is useful and other circumstances in which resonance should be avoided."
• Learning Experiences: The resource suggests various interactive activities for students, such as:
• Examining different graphical representations of SHM.
• Investigating factors affecting the period of oscillations through experiments or simulations. The text explicitly states: "Investigate factors affecting period of oscillations using experiments or a simulation... This provides an opportunity for students to predict and collect data to ascertain the properties of a system and determine whether a motion is considered to be SHM. Students are also to understand that it is necessary for oscillations to be small for the motion to be considered as SHM." This emphasizes the small angle approximation crucial for SHM.
• Investigating phase relationships using turntables or simulations, linking SHM to uniform circular motion.
• Building models of SHM using dataloggers or simulations, focusing on interpreting graphs and understanding variable relationships.
• Exploring real-world applications, such as molecular oscillations (with small amplitudes) and the benefits and dangers of resonance.
• Interactive Simulation: The presence of an "Embed" code (<iframe...>) indicates the resource is designed to be easily integrated into web pages, making it highly accessible for online learning. The "Run Sim" link further confirms the interactive nature.
• Small Angle Approximation: The resource explicitly addresses the limitation of the simple pendulum model for SHM, stating in response to a guiding question: "1.1.2.A1: : 10 degrees for error of , depending on what is the error acceptable, small angle is typically about less than 10 degree of swing from the vertical." This is a crucial point for understanding the validity of the SHM approximation.
• Code Snippets: The inclusion of JavaScript code snippets (e.g., "// prevTime is initialised when the play button is hit...") suggests transparency in the simulation's underlying mechanics, potentially valuable for advanced learners or educators interested in the computational aspects. The equations within the code (e.g., omega += alpha * dt;) illustrate the numerical integration methods likely used for the real-time evolution.
• Links to Other Resources: The presence of numerous links to other pendulum simulations (e.g., from Walter Fendt, Phet Colorado) and related concepts (e.g., Conical Pendulum on GeoGebra) broadens the learning opportunities and provides alternative tools for exploration.
• Applications: The resource mentions applications for various platforms (Android/iOS, Windows/MacOSX/Linux), highlighting its broad compatibility.

Relationship Between the Sources:

While "Pendulum Toy" is presented with less specific detail in the provided excerpt, it likely serves a similar purpose to the "Real Time Evolution Line Code 10 Pendulum" applet – to provide a visual and interactive way to understand pendulum motion. The common authorship (overlapping names in the credits) suggests a potential connection or that both are part of a larger collection of educational physics resources developed by the same team. The "Pendulum Toy" might be a more comprehensive software package, while the "Real Time Evolution" applet is a specific, web-based simulation focusing on SHM aspects.

Educational Implications:

The "Real Time Evolution Line Code 10 Pendulum JavaScript Model Simulation Applet HTML5" is a rich educational resource for teaching oscillations and Simple Harmonic Motion. Its strengths include:

• Clearly defined learning outcomes: Educators can easily align their teaching with the specified objectives.
• Engaging interactive simulation: The ability to run the simulation online and embed it in webpages enhances student engagement and accessibility.
• Emphasis on conceptual understanding: The guiding questions and suggested learning experiences encourage students to explore and interpret the behavior of pendulums.
• Integration of theory and practice: The resource connects theoretical concepts of SHM with visual representations and interactive investigations.
• Addressal of limitations: Explicitly mentioning the small angle approximation is important for developing a nuanced understanding.
• Links to further exploration: The inclusion of links to other simulations and resources allows students to deepen their learning.

Potential Use Cases:

• Classroom demonstrations: Teachers can use the embedded simulation to visually illustrate pendulum motion and its relation to SHM.
• Interactive student activities: Students can explore the simulation independently, investigating the effects of different parameters on the pendulum's period and behavior.
• Homework and self-study: The online accessibility allows students to review concepts and experiment with the simulation outside of the classroom.
• Virtual labs: The simulation can serve as a virtual laboratory environment for exploring oscillatory motion.

Conclusion:

The "Real Time Evolution Line Code 10 Pendulum JavaScript Model Simulation Applet HTML5" is a valuable open educational resource for teaching and learning about pendulums and Simple Harmonic Motion. Its interactive nature, clearly defined learning objectives, and connection to real-world examples make it a powerful tool for educators and students alike. "Pendulum Toy," while less detailed in the provided excerpt, likely complements this resource as a potentially more comprehensive software tool for exploring pendulum dynamics. The shared authorship and Creative Commons licensing further enhance the value and accessibility of these resources for the educational community.

 

Real Time Evolution added by Shaun into the Evolution page

/ Date.now() gets the current UNIX timestamp in milliseconds.
curTime = Date.now();
// prevTime is initialised when the play button is hit. dt measures the time passed between 2 consecutive steps
var dt = (curTime - prevTime) / 1000;

omega += alpha * dt;
theta += omega * dt;
omegas += (-(g/L) * thetas) * dt;
thetas += omegas * dt;

t += dt;

prevTime = curTime;

Apps

https://play.google.com/store/apps/details?id=com.ionicframework.shm01app615913&hl=en

Other Resources

1.  https://www.geogebra.org/m/sux2Q5ak The Conical Pendulum by ukukuku

 

1. http://www.walter-fendt.de/html5/phen/pendulum_en.htm 
2. http://physics.bu.edu/~duffy/HTML5/pendulum.html
3. https://phet.colorado.edu/en/simulation/pendulum-lab 
4. http://www.thephysicsaviary.com/Physics/Programs/Labs/PendulumLab/index.html