About

Bungee Oscillation

Activities

 

Translations

Code	Language		Translator	Run

Credits

Leong Tze Kwang; Lawrence Wee Loo Kang; Francisco Esquembre; Felix Garcia Clemente

 

1. Core Functionality and Purpose:

The primary focus of the described resource is a HTML5 applet built using Javascript that simulates the energy dynamics of a horizontal spring system. The applet includes:

• Visual Representation: An embedded simulation accessible via an iframe: <iframe width="100%" height="100%" src="https://iwant2study.org/lookangejss/02_newtonianmechanics_7energyworkpower/ejss_model_horizontalspring_energy_graph/horizontalspring_energy_graph_Simulation.xhtml " frameborder="0"></iframe>.
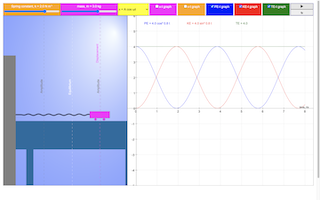
• Energy Graphs: The simulation displays energy graphs as the system is played.
• Displacement and Velocity Graphs: Alongside the energy graphs, the applet includes displacement (x) and velocity (v) over time (t) graphs, indicated by "the 2 dotted lines".
• Adjustable Parameters: Users can interact with the simulation by:
• Maximizing or minimizing the spring constant (k) and the mass (m).
• Changing the initial position and direction using a dropdown box.

The stated Sample Learning Goals (though the specific text is missing in the provided excerpt) indicate its pedagogical purpose in teaching concepts related to energy in a horizontal spring system. The section "For Teachers" further emphasizes its educational utility by providing a "Description: Initial setup" and noting "Energy graphs when played".

2. Context and Development:

• Authorship and Licensing: The applet is credited to Leong Tze Kwang; Lawrence Wee Loo Kang; Francisco Esquembre; Felix Garcia Clemente. It was compiled with EJS 6.1 BETA (200424) and released under a specified license (details not fully provided but likely Creative Commons based on the platform's general licensing). The later excerpt explicitly states the copyright as "© 2020, Leong Tze Kwang; Lawrence Wee Loo Kang; Francisco Esquembre; Felix Garcia Clemente" and confirms it's "Released under a license".
• Open Educational Resource: The applet is hosted under the "Open Educational Resources / Open Source Physics @ Singapore" initiative, highlighting its commitment to freely accessible educational materials.
• Part of a Larger Ecosystem: The applet is categorized under "Newtonian Mechanics" and "Energy Work Power," suggesting it's part of a broader collection of physics simulations. Links to other applets like "Bungee Oscillation" and "Swinging Magnet HTML5 Applet Javascript" indicate a rich library of interactive physics tools.
• Version History: A specific version is mentioned with a link: "https://weelookang.blogspot.com/2020/07/horizontal-spring-energy-graph-html5.html", suggesting ongoing development and potentially accompanying blog posts or explanations.
• EJS Toolkit: The mention of "Easy Java/JavaScript Simulations Toolkit https://www.um.es/fem/EjsWiki/ vy Francisco Esquembre and Félix Jesús Garcia Clemente" highlights the software used for creating the applet and provides a resource for further exploration of similar simulations.

3. Broader Platform and Recognition:

The extensive list of other applets and links within the "Open Educational Resources / Open Source Physics @ Singapore" page reveals a significant and diverse collection of interactive simulations covering various topics in physics, mathematics, chemistry, and even language learning.

Notably, the platform has received external validation: "Recommended in Journal Paper as One of the Top Three Websites for COVID-19 virtual labs education". This suggests the platform and its resources, including potentially this spring energy simulation, have been recognized for their value in remote learning environments.

The inclusion of "2020 Excellence in Physics Education Award from American Physical Society goes to Open Source Physics Team" further underscores the credibility and impact of the group behind these resources.

4. Target Audience and Pedagogical Use:

The categorization under "Physics" and the inclusion of "Sample Learning Goals" and a section "For Teachers" clearly indicate that the primary target audience is students and educators in physics. The interactive nature of the simulation, allowing for manipulation of parameters and observation of real-time graphs, makes it a valuable tool for:

• Visualizing abstract concepts of energy, displacement, and velocity in a simple harmonic motion system.
• Exploring the relationship between spring constant, mass, and the energy dynamics of the system.
• Conducting virtual experiments and gaining an intuitive understanding of these principles.

The presence of other resources on the platform, ranging from primary school science to junior college physics, suggests a broad applicability of the simulations for different educational levels.

5. Technical Aspects:

The use of HTML5 and Javascript ensures that the applet is cross-platform and can be easily accessed through web browsers without the need for additional plugins. The embed code provided facilitates seamless integration into online learning platforms or webpages.

Quotes from the Sources:

• Regarding the simulation display: "Include displacement(x) and velocity(v)-time(t) graphs, represented by the 2 dotted lines"
• Regarding user interaction: "Maximising the spring constant, k and the mass, m Minimising the spring constant, k and the mass, m", "Changing the initial position and direction with the dropdown box"
• Regarding the development toolkit: "Easy Java/JavaScript Simulations Toolkit https://www.um.es/fem/EjsWiki/ vy Francisco Esquembre and Félix Jesús Garcia Clemente"
• Regarding the license and copyright: "Contents are licensed Creative Commons Attribution-Share Alike 4.0 Singapore License.", "© 2020, Leong Tze Kwang; Lawrence Wee Loo Kang; Francisco Esquembre; Felix Garcia Clemente. Compiled with EJS 6.1 BETA (200424) Released under a license."
• Regarding recognition: "Recommended in Journal Paper as One of the Top Three Websites for COVID-19 virtual labs education", "2020 Excellence in Physics Education Award from American Physical Society goes to Open Source Physics Team"

Conclusion:

The "Horizontal spring energy graph HTML5 Applet Javascript" is a valuable open educational resource designed to facilitate the understanding of energy principles in a horizontal spring system. Developed by a recognized team and utilizing accessible web technologies, it offers interactive visualizations and adjustable parameters for effective learning. It is part of a larger, award-winning collection of physics simulations hosted by Open Educational Resources / Open Source Physics @ Singapore, demonstrating a commitment to providing high-quality, freely available educational tools.

 

 

Horizontal Spring Energy Graph Study Guide

Quiz

1. What physical system does the "Horizontal spring energy graph" simulation model?
2. According to the "About" section, what graphs are included in the simulation when it is played?
3. What are the effects of maximizing the spring constant (k) and the mass (m) on the system's behavior as suggested in the "Description"?
4. What are the effects of minimizing the spring constant (k) and the mass (m) on the system's behavior as suggested in the "Description"?
5. Besides adjusting k and m, what other initial conditions can be changed using the dropdown box in the simulation?
6. Who are credited with the development of this simulation, as mentioned in the "Credits" section of the first source and the second source?
7. Under what type of license is the content related to this simulation released, according to the footer of the first source and the second source?
8. What is the intended purpose of the "Sample Learning Goals" section, even though its content is not provided in these excerpts?
9. Where can one find the code for this simulation, as indicated in the first source under "Translations"?
10. What external resource is mentioned in direct relation to this simulation under the "Version" section of the first source?

Quiz Answer Key

1. The "Horizontal spring energy graph" simulation models the behavior of a mass attached to a horizontal spring, likely exploring concepts of energy transfer and oscillation.
2. When played, the simulation includes graphs of displacement (x) versus time (t) and velocity (v) versus time (t), represented by dotted lines.
3. Maximizing the spring constant (k) and the mass (m) will likely result in a higher frequency of oscillation and greater stored energy in the system.
4. Minimizing the spring constant (k) and the mass (m) will likely result in a lower frequency of oscillation and less stored energy in the system.
5. The initial position and direction of the mass can be changed using the dropdown box in the simulation.
6. The credited developers are Leong Tze Kwang, Lawrence Wee Loo Kang, Francisco Esquembre, and Felix Garcia Clemente.
7. The content is licensed under the Creative Commons Attribution-Share Alike 4.0 Singapore License.
8. The "Sample Learning Goals" section is intended to outline the specific educational objectives that users can achieve by interacting with the simulation.
9. The code for the simulation can be found under the "Translations" section, although the specific link or content is not provided in the excerpts.
10. An external blog post by weelookang.blogspot.com is mentioned as a version of this resource.

Essay Format Questions

1. Discuss the relationship between the potential energy stored in the spring and the kinetic energy of the mass in the "Horizontal spring energy graph" simulation. How would changing the spring constant and mass affect the maximum values and transfer between these energy forms?
2. Explain how the displacement versus time graph and the velocity versus time graph relate to the energy graphs displayed in the simulation. How can these graphs be used to understand the points of maximum kinetic and potential energy in the system?
3. Considering the "Sample Learning Goals" and "For Teachers" descriptions (even with limited information), propose three specific learning activities that could utilize this simulation to teach concepts related to simple harmonic motion and energy conservation.
4. Based on the list of "Other Resources" and "Popular Tags," discuss the broader context of this "Horizontal spring energy graph" simulation within the Open Educational Resources / Open Source Physics @ Singapore project. What other physics and mathematics topics appear to be covered by this initiative?
5. Analyze the importance of providing interactive simulations like the "Horizontal spring energy graph" as open educational resources for physics education. What are the potential benefits for both students and teachers compared to traditional teaching methods?

Glossary of Key Terms

• Horizontal Spring: A spring oriented horizontally, typically attached to a mass that can move back and forth along a frictionless surface. This system is often used to model simple harmonic motion.
• Energy Graph: A visual representation showing how different forms of energy (e.g., kinetic energy, potential energy, total mechanical energy) change over time or position in a system.
• HTML5 Applet: An interactive program or application written using HTML5, often incorporating JavaScript for dynamic behavior, that can run directly in a web browser without the need for additional plugins.
• Javascript: A programming language commonly used to add interactivity and dynamic features to websites and web applications, including simulations.
• Open Educational Resources (OER): Teaching, learning, and research materials that are freely available online for anyone to use, adapt, and share, often under open licenses.
• Open Source Physics (OSP): A collaborative project focused on creating and sharing computational tools and resources for physics education, often emphasizing interactive simulations and modeling.
• Displacement (x): The change in position of an object from its equilibrium point. In a spring system, it's the distance the mass has moved from its resting position.
• Velocity (v): The rate of change of displacement with respect to time, indicating how fast and in what direction an object is moving.
• Spring Constant (k): A measure of a spring's stiffness; a higher k value indicates a stiffer spring that requires more force to stretch or compress.
• Mass (m): A measure of the amount of matter in an object, which affects its inertia and response to forces.
• Bungee Oscillation: A type of oscillatory motion involving elastic potential energy and gravitational potential energy, similar in principle to a mass-spring system but often in a vertical orientation with a bungee cord.
• Newtonian Mechanics: The branch of classical mechanics that describes the motion of macroscopic objects at non-relativistic speeds using Newton's laws of motion.
• Energy Work Power: A fundamental area of physics dealing with concepts of energy, the ability to do work, and the rate at which work is done (power).
• Initial Position: The starting location of the mass in the simulation at the beginning of its motion.
• Initial Direction: The starting direction of the velocity of the mass in the simulation at the beginning of its motion.
• Simple Harmonic Motion: A type of periodic motion where the restoring force is directly proportional to the displacement and acts in the direction opposite to that of displacement. An ideal horizontal spring-mass system exhibits simple harmonic motion.
• Kinetic Energy: The energy possessed by an object due to its motion, proportional to its mass and the square of its velocity.
• Potential Energy: The energy stored in an object due to its position or configuration. In a spring system, this is the elastic potential energy stored when the spring is stretched or compressed.
• Total Mechanical Energy: The sum of the kinetic energy and potential energy in a system, which is conserved in the absence of non-conservative forces like friction

Sample Learning Goals

[text]

For Teachers

Initial setup

 

Energy graphs when played

 

Include displacement(x) and velocity(v)-time(t) graphs, represented by the 2 dotted lines

Maximising the spring constant, k and the mass, m

Minimising the spring constant, k and the mass, m

Changing the initial position and direction with the dropdown box

Research

[text]

Video

[text]

 Version:

1. https://weelookang.blogspot.com/2020/07/horizontal-spring-energy-graph-html5.html

Other Resources

[text]