About

Projectile Motion with System of Masses and Spring

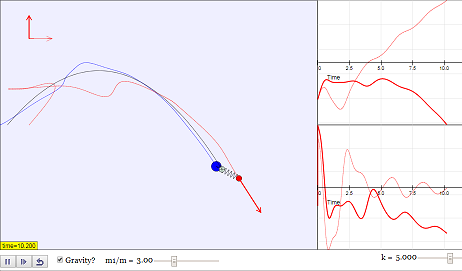
This is the simulation of the motion of two masses m and m₁ situated at the ends of a spring of length L₀ and negligible mass. The motion is restricted to two spatial dimensions, with the y-axis representing the vertical (if gravity is switched on).

We use Hooke's law for the spring force, and include a damping term that is proportional to the difference of the velocities of the masses on both ends of the spring. You can also choose for the spring to behave like a spring only when stretched, and have no effect when compressed (i.e. it is more like a string).

Applying Newton's Second Law yields a second-order ordinary differential equation, which we solve numerically in the simulation and visualise the results.

Activities

1. Drag the red mass to impart an initial velocity, and see how the system evolves.
2. Observe what happens when you do the same, but with gravity switched on.
3. Try changing the relative mass of the blue ball, and notice how the centre of gravity shifts.
4. Try varying the spring constant and/or the damping coefficient while the simulation runs.
5. Also try activating the "string-like" mode such that the elastic force only occurs in the stretched state and not in the compressed state.

 

Translations

Code	Language		Translator	Run

Credits

Wolfgang Christian; Francisco Esquembre; Zhiming Darren TAN

Overview:

This briefing document reviews a physics simulation focused on the projectile motion of a system involving two masses connected by a spring. The simulation, developed using HTML5 and JavaScript, is an open educational resource designed for learning and experimentation with concepts such as Newton's Second Law, Hooke's Law, gravity, oscillations, and the center of gravity.

Main Themes and Important Ideas/Facts:

• Simulation of a Two-Mass Spring System in 2D: The core of the resource is an interactive simulation that models the movement of two masses (m and m1) connected by a spring with an initial length L0 and negligible mass. The motion is constrained to two spatial dimensions (x and y), with the y-axis representing the vertical direction where gravity can be enabled.
• As stated in the "About" section, "This is the simulation of the motion of two masses m and m1 situated at the ends of a spring of length L0 and negligible mass. The motion is restricted to two spatial dimensions, with the y-axis representing the vertical (if gravity is switched on)."
• Incorporation of Physical Laws: The simulation applies fundamental physics principles:
• Hooke's Law: The spring force is modeled using Hooke's Law, which states that the force exerted by a spring is proportional to its displacement from its equilibrium position.
• The description notes, "We use Hooke's law for the spring force..."
• Newton's Second Law: The motion of the masses is governed by Newton's Second Law of Motion (F=ma), which relates the net force acting on an object to its mass and acceleration. The simulation numerically solves the resulting second-order ordinary differential equation.
• The text explicitly mentions, "Applying Newton's Second Law yields a second-order ordinary differential equation, which we solve numerically in the simulation and visualise the results."
• Gravity: Users can toggle gravity on or off to observe its effect on the projectile motion of the mass-spring system.
• One of the "Activities" encourages users to "Observe what happens when you do the same, but with gravity switched on."
• Damping: The simulation includes a damping force that is proportional to the relative velocity of the two masses, allowing for the exploration of energy dissipation.
• The description states, "...and include a damping term that is proportional to the difference of the velocities of the masses on both ends of the spring."
• "String-like" Behavior: The simulation offers a mode where the spring only exerts a force when stretched, mimicking the behavior of a string. In this mode, there is no restoring force when the masses move closer than the spring's natural length.
• Users are encouraged to "Try also activating the 'string-like' mode such that the elastic force only occurs in the stretched state and not in the compressed state."
• Interactive Exploration and Learning: The resource is designed for active learning through various interactive elements:
• Initial Velocity: Users can drag the red mass to impart an initial velocity to the system and observe its subsequent motion.
• The first activity listed is to "Drag the red mass to impart an initial velocity, and see how the system evolves."
• Mass Variation: Users can change the relative mass of the blue ball and observe how this affects the system's center of gravity.
• Another activity suggests, "Try changing the relative mass of the blue ball, and notice how the centre of gravity shifts."
• Parameter Adjustment: During the simulation, users can modify the spring constant and the damping coefficient to see their impact on the motion.
• Users are prompted to "Try varying the spring constant and/or the damping coefficient while the simulation runs."
• Open Educational Resource: The simulation is part of the Open Educational Resources / Open Source Physics @ Singapore initiative, making it freely accessible for educational purposes. It is licensed under the Creative Commons Attribution-Share Alike 4.0 Singapore License.
• The website clearly states "Open Educational Resources / Open Source Physics @ Singapore" and mentions the licensing terms at the bottom of the page. The "Masses and Spring Projectile" document also explicitly states it is "Released under a license."
• Embeddability: The simulation can be easily embedded into other web pages using an iframe code provided on the page.
• The page offers an "Embed this model in a webpage:" section with the iframe code.
• Credits and Development: The simulation is credited to Wolfgang Christian, Francisco Esquembre, and Zhiming Darren TAN, indicating a collaborative effort in its creation. The "Masses and Spring Projectile" document also acknowledges these authors and specifies it was "Compiled with EJS 6.0".
• Potential Learning Goals: While the specific learning goals are not detailed in the provided excerpts, the activities suggest that students can learn about:
• The relationship between initial conditions and projectile motion.
• The influence of gravity on a connected mass system.
• The concept and shifting of the center of gravity.
• The effect of spring constant and damping on oscillations and motion.
• The difference between a spring and a string in terms of force application.

Quotes from Sources:

• On the simulation's core functionality: "This is the simulation of the motion of two masses m and m1 situated at the ends of a spring of length L0 and negligible mass." (Open Educational Resources / Open Source Physics @ Singapore)
• On the forces involved: "We use Hooke's law for the spring force, and include a damping term that is proportional to the difference of the velocities of the masses on both ends of the spring." (Open Educational Resources / Open Source Physics @ Singapore)
• On the application of Newton's Laws: "Applying Newton's Second Law yields a second-order ordinary differential equation, which we solve numerically in the simulation and visualise the results." (Open Educational Resources / Open Source Physics @ Singapore)
• On user interaction: "Drag the red mass to impart an initial velocity, and see how the system evolves." (Open Educational Resources / Open Source Physics @ Singapore)
• On the open nature of the resource: "Contents are licensed Creative Commons Attribution-Share Alike 4.0 Singapore License ." (Open Educational Resources / Open Source Physics @ Singapore)

Conclusion:

The "Mass and Spring in Projectile Motion" simulation is a valuable open educational resource for teaching and learning fundamental physics concepts related to mechanics, oscillations, and gravity. Its interactive nature allows students to actively explore the behavior of a coupled mass-spring system under various conditions, providing a visual and engaging way to understand the application of physical laws. The ability to adjust parameters and observe the resulting motion fosters deeper conceptual understanding.

 

Mass and Spring in Projectile Motion Study Guide

Key Concepts

• Projectile Motion: The motion of an object under the influence of gravity. Typically involves a parabolic trajectory.
• Mass: A fundamental property of an object that measures its resistance to acceleration when a net force is applied. Represented by m and m1 in the simulation.
• Spring Force (Hooke's Law): The restoring force exerted by a spring that is proportional to its displacement from its equilibrium length. Mathematically expressed as F = -k(x - L0), where k is the spring constant, x is the current length, and L0 is the equilibrium length.
• Spring Constant (k): A measure of the stiffness of a spring. A higher spring constant indicates a stiffer spring that requires more force to stretch or compress.
• Damping: A force that opposes motion and dissipates energy from a system, often proportional to velocity. In this simulation, it's proportional to the difference in velocities of the two masses.
• Equilibrium Length (L0): The natural, unstretched length of the spring.
• Centre of Gravity: The point at which the weight of an object is considered to act. For a system of masses, the centre of gravity's position depends on the individual masses and their locations.
• Newton's Second Law of Motion: States that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass (F = ma). This law is applied to each mass in the simulation.
• Second-Order Ordinary Differential Equation: A type of mathematical equation that describes the motion of the system by relating the positions, velocities, and accelerations of the masses over time. These equations are solved numerically by the simulation.
• Numerical Solution: An approximate solution to a mathematical problem obtained through computational methods, often used when an analytical solution is difficult or impossible to find.
• Two Spatial Dimensions: Motion that occurs within a plane, requiring two coordinates (typically x and y) to describe the position of an object.
• Stretched State: When the length of the spring is greater than its equilibrium length (x > L0).
• Compressed State: When the length of the spring is less than its equilibrium length (x < L0).
• String-like Mode: A setting in the simulation where the spring only exerts a force when it is stretched, acting like an inextensible string when compressed (no restoring force).

Quiz

1. Describe the physical system being modeled in the simulation. What are the main components and how are they connected?
2. Explain the role of Hooke's Law in the simulation. How does the spring force affect the motion of the two masses?
3. What is the purpose of the damping term included in the simulation? How does it influence the system's behavior over time?
4. How does changing the relative mass of the two balls affect the system's centre of gravity? Explain the relationship.
5. In the simulation activities, what happens when gravity is switched on while the system is in motion? How does gravity alter the trajectory?
6. What are the observable effects of varying the spring constant in the simulation? How does a higher or lower spring constant change the system's behavior?
7. Explain the "string-like" mode option. How does the system's behavior differ when this mode is activated compared to when the spring acts normally under both stretching and compression?
8. According to the text, how are the equations of motion for this system solved? Why is this method used?
9. What are some of the interactive activities suggested for exploring the simulation? Briefly describe two of them.
10. What fundamental physics principle is directly applied to derive the equations governing the motion of the masses and spring system?

Quiz Answer Key

1. The simulation models a system of two masses (m and m1) connected by a spring with an equilibrium length L0 and negligible mass. The motion of these masses is restricted to two spatial dimensions (x and y).
2. Hooke's Law describes the spring force, which acts to restore the spring to its equilibrium length. This force acts on both masses, pulling them together when stretched and pushing them apart when compressed (unless in "string-like" mode).
3. The damping term represents a force that opposes the relative motion of the two masses connected by the spring. It causes the oscillations of the system to decrease in amplitude over time, eventually bringing the system to a state of rest or equilibrium.
4. Changing the relative mass of the blue ball shifts the centre of gravity of the two-mass system towards the more massive object. The centre of gravity is a weighted average of the positions of the masses.
5. When gravity is switched on, the trajectory of the system as a whole will be influenced by the downward gravitational force, causing it to follow a parabolic path, similar to a standard projectile. The internal oscillations due to the spring will be superimposed on this overall motion.
6. Varying the spring constant affects the frequency of oscillations in the system. A higher spring constant results in a higher frequency of oscillation (faster back and forth movement), while a lower spring constant leads to a lower frequency.
7. In "string-like" mode, the spring only exerts a restoring force when it is stretched. When the masses move close enough to compress the spring, no elastic force is generated, and the masses may move independently until the spring becomes stretched again.
8. The equations of motion, which are second-order ordinary differential equations derived from Newton's Second Law, are solved numerically in the simulation. This is likely because the coupled motion of the two masses and the spring force can lead to complex equations that are difficult to solve analytically.
9. Two suggested activities are: (1) Dragging the red mass to impart an initial velocity and observing the system's evolution, and (2) Observing the effect of switching gravity on after imparting an initial velocity.
10. Newton's Second Law of Motion (F = ma) is the fundamental physics principle applied to each mass in the system to derive the second-order ordinary differential equations that govern their motion under the influence of the spring force, damping, and gravity (if enabled).

Essay Format Questions

1. Discuss how the interplay between the spring force, gravity, and initial conditions determines the complex trajectory of the two-mass system in the simulation. Consider scenarios with and without damping, and with varying relative masses.
2. Analyze the energy transformations within the mass-spring projectile system. How does the initial kinetic energy imparted to one mass get distributed and potentially dissipated over time, considering the roles of the spring potential energy and damping?
3. Compare and contrast the behavior of the system when the spring acts as a traditional elastic element versus when it is set to the "string-like" mode. Under what conditions would the differences in motion be most significant?
4. Explain how the concept of the centre of gravity applies to the two-mass system connected by a spring. How does the motion of the centre of gravity relate to the external forces acting on the system, such as gravity?
5. Describe the educational value of this simulation for understanding the principles of projectile motion, oscillations, and the application of Newton's Laws. How can the interactive features enhance student learning in physics?

Glossary of Key Terms

• Damping Coefficient: A numerical value that quantifies the strength of the damping force in a system. A higher coefficient indicates stronger damping.
• Force: An interaction that, when unopposed, will change the motion of an object. It has both magnitude and direction (a vector quantity).
• Gravity: The force of attraction between objects with mass. Near the Earth's surface, it causes objects to accelerate downwards at approximately 9.8 m/s².
• Kinetic Energy: The energy possessed by an object due to its motion. It depends on the object's mass and velocity.
• Open Educational Resources (OER): Teaching, learning, and research materials that are freely available and can be reused, remixed, revised, and redistributed.
• Oscillation: A repetitive variation, typically in time, of some measure about a central value or between two or more different states.
• Potential Energy (Spring): The energy stored in a spring due to its deformation (stretching or compression) from its equilibrium length.
• Trajectory: The path followed by a projectile or other moving object.
• Velocity: The rate of change of an object's position with respect to time and a frame of reference. It is a vector quantity, having both speed and direction.

Sample Learning Goals

[text]

For Teachers

[text]

Research

[text]

Video

[text]

 Version:

1. https://weelookang.blogspot.com/2020/10/mass-and-spring-in-projectile-motion.html

Other Resources

[text]

Frequently Asked Questions: Mass and Spring Projectile Simulation

1. What does this simulation demonstrate?

This simulation visualizes the motion of a system consisting of two masses connected by a spring in two spatial dimensions. It allows users to observe projectile motion principles in conjunction with the forces exerted by a spring, including Hooke's Law. The simulation also incorporates the effects of gravity (which can be toggled on or off) and a damping force.

2. What physical principles are at play in this simulation?

Several fundamental physics principles are involved. These include Newton's Second Law of Motion, which governs the acceleration of the masses based on the net force acting on them. Hooke's Law describes the spring force, which is proportional to the displacement from its equilibrium length. Gravity exerts a constant downward force on the masses when enabled. Additionally, the simulation models a damping force proportional to the relative velocity of the two masses.

3. How can I interact with the simulation?

Users can interact with the simulation in several ways. They can drag the red mass to impart an initial velocity to the system. They can toggle gravity on or off to observe its effect. The relative mass of the blue ball can be changed, allowing observation of how this affects the center of gravity and the system's motion. Users can also vary the spring constant and the damping coefficient while the simulation is running to see their influence on the oscillations and overall movement. Finally, a "string-like" mode can be activated, where the spring only exerts a force when stretched, not when compressed.

4. What can I learn by observing the simulation with gravity?

By observing the simulation with gravity enabled, you can see how the familiar parabolic trajectory of projectile motion is affected by the presence of the spring connecting the two masses. The system will exhibit both a general projectile motion of its center of mass and oscillations due to the spring force. You can observe how gravity influences the vertical motion of the masses and the interplay between the gravitational force and the spring force.

5. How does changing the relative mass of the two balls affect the system?

Changing the relative mass of the blue ball shifts the center of gravity of the two-mass system. This shift influences the overall trajectory of the system under the influence of gravity and affects the way the two masses move relative to each other due to the spring force. The more massive object will have a greater influence on the system's overall momentum and inertia.

6. What is the effect of varying the spring constant and damping coefficient?

The spring constant determines the stiffness of the spring. A higher spring constant will result in stronger restoring forces when the spring is stretched or compressed, leading to higher frequency oscillations. The damping coefficient introduces a force that opposes the relative motion of the two masses, causing the oscillations to decrease in amplitude over time. A higher damping coefficient will lead to a faster decay of oscillations.

7. What is the "string-like" mode and how does it differ from a regular spring?

In the "string-like" mode, the spring behaves like a typical spring when it is stretched, exerting a restoring force proportional to the extension. However, unlike a regular spring, it exerts no force when it is compressed. This means the masses can move closer to each other freely until the spring becomes taut again, at which point it starts to exert a tensile force. This introduces a non-linear behavior to the system's dynamics.

8. What educational purposes does this simulation serve?

This simulation is designed as an open educational resource for teaching and learning physics concepts related to projectile motion, oscillations, Newton's Laws, and Hooke's Law. It allows students to visualize the interplay of these concepts in a dynamic system and to explore how changing parameters like mass, spring constant, damping, and gravity affect the motion. The activities suggested encourage active learning and experimentation.