Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits


 This email address is being protected from spambots. You need JavaScript enabled to view it.; Francisco Esquembre; Felix J. Garcia Clemente
This email address is being protected from spambots. You need JavaScript enabled to view it.; Francisco Esquembre; Felix J. Garcia Clemente
Overview:
This briefing document summarizes the main themes and important ideas presented in two related educational resources focused on teaching primary school students about numbers from 1 to 100, with a specific emphasis on even/odd numbers, multiples, and factors. Both sources appear to be connected, with overlapping authors and a shared focus on utilizing interactive simulations (specifically JavaScript HTML5 applets) to enhance learning. The materials align with primary mathematics curricula, particularly for students in Primary 3, 4, and 5 Foundation Mathematics.
Main Themes and Important Ideas:
- Focus on Foundational Number Concepts: Both resources center on building a strong understanding of basic number properties within the range of 1 to 100. The core concepts addressed are:
- Even and Odd Numbers: The resources highlight the definition of even numbers as those that can be paired and odd numbers as those with a "lonely one" when paired. A poem is included to illustrate this concept:
- "If you are an even number You always have a pair So if you look around Your buddy will always be there But ... If you are an odd number There's always a lonely one He looks around to find his buddy But he's the only one." - Marg Wadsworth
- Multiples: Multiples are presented as the result of "skip count[ing]," making it easier for students to grasp. For example, "multiples of three is skip count three, for example, 3, 6, 9, 12, ...." The resource emphasizes the use of color-coding in simulations to aid pattern recognition for multiples.
- Factors: Factors are identified as a more challenging concept. A strategy suggested is "pairing the first and the last numbers of the factors could help pupils realise." The resource also notes the use of color-coding to show the pairing of factors (e.g., 1x48 = 2x24 = 3x16 = 4x12 = 6x8 = 48).
- Alignment with Primary School Curriculum: The "Primary School Numbers from 1 to 100..." resource explicitly mentions its alignment with the Singaporean primary mathematics curriculum:
- Primary 3: Includes "odd and even numbers," and "number patterns" within the topic of "WHOLE NUMBERS Numbers up to 10 000."
- Primary 4: Focuses on "Factors and multiples," including "determining if a 1-digit number is a factor of a given number," "listing all factors of a given number up to 100," "finding the common factors of two given numbers," "recognising the relationship between factor and multiple," "determining if a number is a multiple of a given 1-digit number," "listing the first 12 multiples of a given 1-digit number," and "finding the common multiples of two given 1-digit numbers." Notably, it excludes "highest common factor' (H.C.F.) and 'lowest common multiple’ (L.C.M.)."
- Primary 5 Foundation Mathematics: Revisits "Factors and multiples" with similar inclusions as Primary 4 but specifies "finding the common multiples of two given numbers up to 12." Again, "highest common factor' (H.C.F.) and 'lowest common multiple’ (L.C.M.)" are excluded.
- Interactive Learning through Simulations: A significant aspect of these resources is the emphasis on using JavaScript HTML5 applet simulations. The "Primary School Numbers from 1 to 100..." source provides an embeddable model and links to accompanying apps for various platforms (Android, iOS, Windows, MacOSX, Linux, ChromeBook). This highlights the intention to provide accessible and interactive learning experiences.
- Practical Application and Problem Solving: The "Primary School Numbers from 1 to 100..." resource includes sample questions to test understanding of multiples and factors in real-world scenarios. Examples include:
- "I am a multiple of 7. I am between 50 to 100. The digit in the tens place is 0. What am I? Answer 70"
- "I am a factor of 30. When you round me to the nearest tens place, you get 20. What number am I? Answer: 15"
- Word problems involving the greatest common factor (though H.C.F. is formally excluded from the curriculum topics listed):
- "Miss Lim has 36 pens and 54 pencils. She distributed them equally among her students.What is the greatest number of students that Miss Lim can have?" The suggested steps demonstrate finding the greatest common factor by listing factors and identifying the largest common one: "Factors of 36: 1, 2, 3, 4, 9, 12, 18, and 36 Factors of 54: 1, 2, 3, 6, 9, 18, 27, and 54 The common factors are: 1, 2, 3, 9, and 18 The greatest common factor is 18 Answer: 18"
- Teaching Tips and Strategies: The resource offers practical teaching tips, such as using physical pairing activities to illustrate even and odd numbers:
- For even numbers: "ask pupils to line up in pairs, so if it is possible to pair up, the number of pupils is even."
- For odd numbers: "ask pupils to line up in pairs, so if it is not possible to pair up, meaning one pupil has no partner, the number of pupils is odd."
- Open Educational Resources: The "Primary School Numbers from 1 to 100..." source clearly identifies itself as part of "Open Educational Resources / Open Source Physics @ Singapore." The content is licensed under a Creative Commons Attribution-Share Alike 4.0 Singapore License, promoting sharing and adaptation. However, it also notes specific conditions for commercial use of the "EasyJavaScriptSimulations Library."
- Connections to Other Resources: The "Primary School Numbers from 1 to 100..." page provides numerous links to related resources, including other simulations, apps, blog posts, and even conference materials. This suggests a broader ecosystem of educational tools developed by the authors and their collaborators.
Conclusion:
These resources provide a comprehensive and interactive approach to teaching fundamental number concepts (even/odd, multiples, and factors) to primary school students, particularly those following the Singaporean mathematics curriculum. The emphasis on visual aids through color-coding and engaging simulations via JavaScript HTML5 applets makes learning more accessible and potentially more effective. The inclusion of practical teaching tips, sample problems, and links to further resources positions these materials as valuable tools for educators. The open educational resource nature further enhances their potential for widespread use and adaptation.
Study Guide: Numbers 1-100 - Factors and Multiples
Core Concepts
- Whole Numbers: Understanding the set of positive integers (1, 2, 3, ...). The context here is whole numbers up to 100.
- Even Numbers: Whole numbers divisible by 2 (e.g., 2, 4, 6...).
- Odd Numbers: Whole numbers not divisible by 2 (e.g., 1, 3, 5...).
- Factors: Whole numbers that divide evenly into another whole number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12.
- Multiples: The result of multiplying a whole number by another whole number. For example, the multiples of 3 are 3, 6, 9, 12, and so on.
- Common Factors: Factors that are shared by two or more numbers. For example, the common factors of 12 and 18 are 1, 2, 3, and 6.
- Common Multiples: Multiples that are shared by two or more numbers. For example, some common multiples of 2 and 3 are 6, 12, and 18.
- Greatest Common Factor (GCF): The largest factor that two or more numbers share. (Note: This is excluded from the primary learning goals but is exemplified in the "Miss Lim" question.)
- Lowest Common Multiple (LCM): The smallest multiple that two or more numbers share. (Note: This is excluded from the primary learning goals.)
- Number Patterns: Recognizing and extending sequences of numbers based on a rule (e.g., even numbers, multiples of 5).
- Place Value: Understanding the value of a digit based on its position in a number (ones, tens, hundreds).
Key Learning Goals (Primary School Focus)
- Identify and differentiate between odd and even numbers.
- Determine if a 1-digit number is a factor of a given number.
- List all factors of a given number up to 100.
- Find the common factors of two given numbers.
- Recognize the relationship between factors and multiples.
- Determine if a number is a multiple of a given 1-digit number.
- List the first 12 multiples of a given 1-digit number.
- Find the common multiples of two given 1-digit numbers.
- Apply the concepts of factors and multiples to solve simple word problems.
Review Questions
- Explain the difference between an even number and an odd number using the concept of pairing.
- List all the factors of the number 24. Describe the strategy you used to find them.
- What are the first five multiples of the number 6? How are multiples related to skip counting?
- Find two common factors of the numbers 15 and 20. Explain how you identified these common factors.
- Describe the relationship between the number 8, its factors (1, 2, 4, 8), and its multiples (8, 16, 24...).
- Is the number 42 a multiple of 7? Explain your reasoning.
- List the common multiples of 3 and 4 up to the number 50.
- Explain how understanding place value can help in identifying even and odd numbers.
- Consider the number 35. Is it a factor or a multiple of 5? Is 5 a factor or a multiple of 35? Explain.
- How can the concept of factors be used to solve the word problem about Miss Lim's pens and pencils, even though the term "greatest common factor" is excluded from the primary goals?
Quiz
Instructions: Answer the following questions in 2-3 sentences each.
- Define what a factor of a number is. Provide an example with the number 10.
- Explain the concept of a multiple. Give three examples of multiples of the number 9.
- How can you determine if a whole number is even? Describe a method you can use.
- What does it mean for two numbers to have a common factor? Provide an example using the numbers 6 and 8.
- Describe the relationship between factors and multiples using the numbers 4 and 12.
- Explain how to list the first few multiples of a given single-digit number, such as 5.
- What is a common multiple of two numbers? Give an example using the numbers 2 and 5.
- How can you identify all the factors of a number up to 100? Briefly outline a strategy.
- If a number ends in 0, 2, 4, 6, or 8, what can you conclude about that number? Explain why.
- In a problem where you need to divide items equally among a group, how might the concept of factors be helpful?
Quiz Answer Key
- A factor of a number is a whole number that divides evenly into that number without leaving a remainder. For example, the factors of 10 are 1, 2, 5, and 10 because 10 divided by each of these numbers results in a whole number.
- A multiple of a number is the result of multiplying that number by any whole number. Three examples of multiples of 9 are 9 (9 x 1), 18 (9 x 2), and 27 (9 x 3).
- A whole number is even if it can be divided by 2 with no remainder. You can also determine if a number is even by looking at its last digit; if the last digit is 0, 2, 4, 6, or 8, the number is even.
- Two numbers have a common factor if there is a whole number that divides evenly into both of them. For example, the numbers 6 and 8 have a common factor of 2 because 6 divided by 2 is 3, and 8 divided by 2 is 4.
- Factors divide a number evenly, while a number is a multiple of its factors. In the case of 4 and 12, 4 is a factor of 12 because 12 divided by 4 is 3. Conversely, 12 is a multiple of 4 because it can be obtained by multiplying 4 by 3.
- To list the first few multiples of a single-digit number like 5, you start by multiplying 5 by 1, then by 2, then by 3, and so on. The first few multiples of 5 are 5 (5x1), 10 (5x2), 15 (5x3), 20 (5x4), and 25 (5x5).
- A common multiple of two numbers is a number that is a multiple of both of those numbers. For example, a common multiple of 2 and 5 is 10 because 10 is a multiple of 2 (2 x 5 = 10) and also a multiple of 5 (5 x 2 = 10).
- To identify all the factors of a number up to 100, you can systematically check each whole number from 1 up to that number to see if it divides evenly. Pairing factors (e.g., for 24: 1x24, 2x12, 3x8, 4x6) can also help ensure you find all the factors.
- If a number ends in 0, 2, 4, 6, or 8, you can conclude that the number is an even number. This is because these digits represent a quantity that is divisible by 2, and therefore, any whole number ending in these digits is also divisible by 2.
- In a problem involving equal division, the concept of factors helps determine the possible sizes of the groups or the number of groups that can be formed without any remainder. Finding common factors of the quantities being divided can help find the largest possible equal groups.
Essay Format Questions
- Discuss the interconnectedness of the concepts of factors and multiples. Provide examples to illustrate their relationship and explain why understanding this relationship is fundamental in mathematics.
- Explain how the ability to identify even and odd numbers, and to find factors and multiples, builds a foundation for more advanced mathematical topics encountered in later primary school years. Reference specific learning goals mentioned in the provided sources.
- Describe different strategies that can be used to help primary school students understand the concepts of factors and multiples. Incorporate ideas from the "Teaching Tips" section of the provided materials in your response.
- Analyze the sample word problems provided in the source material. Explain how these problems effectively assess a student's understanding of factors and multiples within the context of real-world scenarios.
- Consider the range of numbers from 1 to 100. Discuss the patterns and relationships that emerge when examining the factors and multiples of these numbers, and how exploring these patterns can enhance number sense in primary students.
Glossary of Key Terms
- Factor: A whole number that divides exactly into another whole number without leaving a remainder.
- Multiple: A number that can be obtained by multiplying a given whole number by another whole number.
- Even Number: A whole number that is divisible by 2.
- Odd Number: A whole number that is not divisible by 2.
- Common Factor: A factor that is shared by two or more numbers.
- Common Multiple: A multiple that is shared by two or more numbers.
- Whole Number: Any of the non-negative integers (0, 1, 2, 3, ...). In this context, primarily refers to positive integers (1, 2, 3, ...) as per the source.
- Place Value: The numerical value that a digit has by virtue of its position in a number.
- Digit: Any of the numerals from 0 to 9 used to form numbers.
- Divisible: Capable of being divided by another number without a remainder.
Apps
https://play.google.com/store/apps/details?id=com.ionicframework.numbers100app321231

https://play.google.com/store/apps/details?id=com.ionicframework.numbersapp974975 older version
https://itunes.apple.com/us/app/even-odd-multiples-factors/id1196575475?ls=1&mt=8 iOS version
Sample Learning Goals
Topics
Primary 3
1 WHOLE NUMBERS
Numbers up to 10 000
Include:
• number notation and place values (thousands, hundreds, tens, ones),
• reading and writing numbers in numerals and in words,
• comparing and ordering numbers,
• odd and even numbers,
• number patterns
Primary 4
1 Whole Numbers
Factors and multiples
Include:
• determining if a 1-digit number is a factor of a given number,
• listing all factors of a given number up to 100,
• finding the common factors of two given numbers,
• recognising the relationship between factor and multiple,
• determining if a number is a multiple of a given 1-digit number,
• listing the first 12 multiples of a given 1-digit number,
• finding the common multiples of two given 1-digit numbers.
Exclude 'highest common factor' (H.C.F.) and 'lowest common multiple’ (L.C.M.).
Primary 5 Foundation Mathematics (Calculator is allowed unless otherwise stated)
1 Whole Numbers
Factors and multiples
Include:
• determining if a 1-digit number is a factor of a given number,
• listing all factors of a given number up to 100,
• finding the common factors of two given numbers,
• recognising the relationship between factor and multiple,
• determining if a number is a multiple of a given 1-digit number,
• listing the first 12 multiples of a given 1-digit number,
• finding the common multiples of two given numbers up to 12.
Exclude 'highest common factor' (H.C.F.) and 'lowest common multiple’ (L.C.M.).
Questions:
 |
| I am a multiple of 7. I am between 50 to 100. The digit in the tens place is 0. What am I? Answer 70 |
 |
| I am a factor of 30. When you round me to the nearest tens place, you get 20. What number am I? Answer: 15 |
 |
| Miss Lim has 36 pens and 54 pencils. She distributed them equally among her students.What is the greatest number of students that Miss Lim can have? Answer: 18 |
 |
| Miss Lim has 36 pens and 54 pencils. She distributed them equally among her students.What is the greatest number of students that Miss Lim can have? Suggested steps: Factors of 36: 1, 2, 3, 4, 9, 12, 18, and 36 Factors of 54: 1, 2, 3, 6, 9, 18, 27, and 54 The common factors are: 1, 2, 3, 9, and 18 The greatest common factor is 18 Answer: 18 |
Research
SSTRF_2017_ETD_3 Explore-Useful Learning Math Apps
Teaching Tips
even numbers are easier to understand, ask pupils to line up in pairs, so if it is possible to pair up, the number of pupils is even.
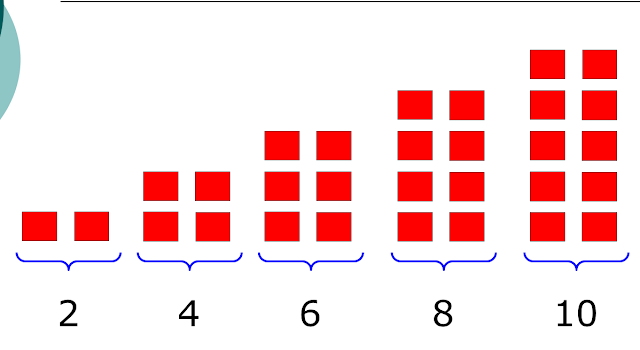 |
| taken from http://library.opal.moe.edu.sg/cos/o.x?ptid=84&c=/library/reslib&func=prop2&id=148606 by Abdul Hakim Bin Mohd Udori |
odd numbers is the opposite of even, again, ask pupils to line up in pairs, so if it is not possible to pair up, meaning one pupil has no partner, the number of pupils is odd.
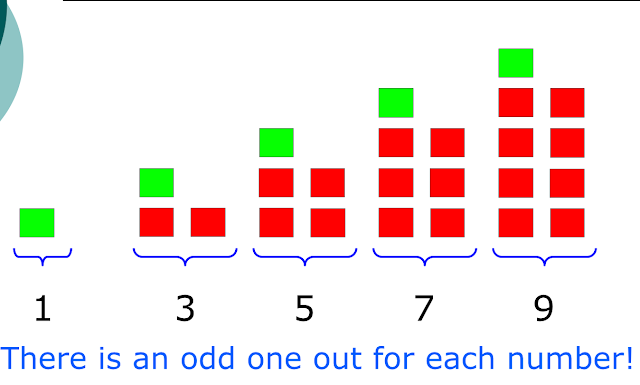 |
| taken from http://library.opal.moe.edu.sg/cos/o.x?ptid=84&c=/library/reslib&func=prop2&id=148606 by Abdul Hakim Bin Mohd Udori |
A Poem on Even & Odd Numbers by Marg Wadsworth
If you are an even number
You always have a pair
So if you look around
Your buddy will always be there
But ...
If you are an odd number
There's always a lonely one
He looks around to find his buddy
But he's the only one.
YouTube
10 Odd Todd and Even Steven swerdy45
multiples is easier if it is associated to skip count, so mulitples of three is skip count three, for example, 3 ,6, 9, 12, ....
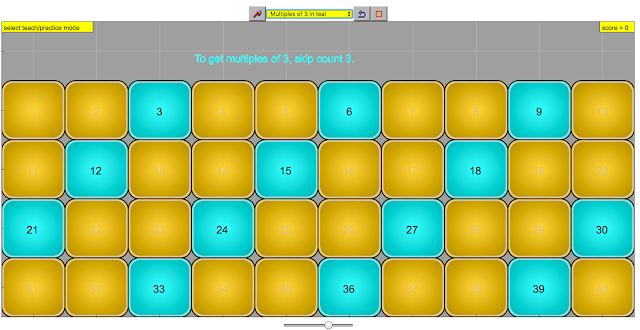 |
| multiples of three, skip count three, color coded for ease of pattern recognition |
factors is the hardest, pairing the first and the last numbers of the factors could help pupils realise
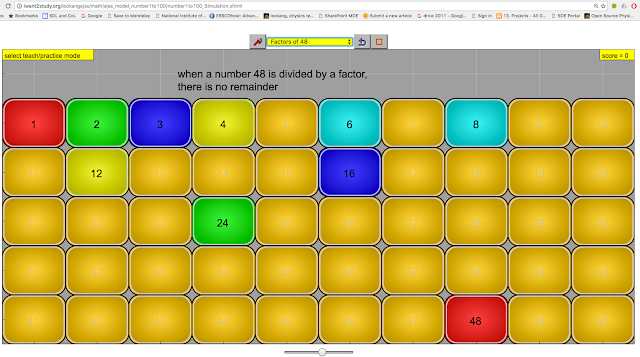 |
| factors of a numbers colour coded for ease of pattern recognition 1x48 = 2x24 = 3x16 = 4x12 = 6x8 = 48 |
Video
[text]
Version:
- https://weelookang.blogspot.com/2021/08/primary-school-numbers-from-1-to-100.html
- http://weelookang.blogspot.sg/2016/06/numbers-1-to-100-properties.html JavaScript version
- based on an earlier swf file from Thong , Thong's files
- http://library.opal.moe.edu.sg/cos/o.x?c=/library/reslib&uid=0&ptid=84&func=view&id=266009&fext=.zip (login required)
Other Resources
Frequently Asked Questions about Numbers 1-100 for Primary Math
1. What mathematical concepts related to numbers up to 100 are emphasized for primary school students based on these resources?
These resources primarily focus on foundational number concepts for primary school mathematics, specifically for numbers ranging from 1 to 100. Key areas include understanding odd and even numbers, identifying multiples of single-digit numbers, listing all factors of a given number (up to 100), finding common factors and common multiples of two numbers (mainly single-digit for multiples), and recognizing the relationship between factors and multiples. The curriculum examples also mention number notation, place values, reading and writing numbers, comparing and ordering numbers, and identifying number patterns.
2. How do these materials suggest teaching the concepts of even and odd numbers to young learners?
The materials suggest using practical, visual methods to teach even and odd numbers. A recommended teaching tip involves asking pupils to line up in pairs. If everyone has a partner, the number is even. If one pupil is left without a partner, the number is odd. A poem is also provided as a supplementary resource, reinforcing the idea of even numbers having pairs and odd numbers having a "lonely one."
3. What strategies are recommended for teaching multiples effectively?
The resources suggest associating multiples with skip counting. For instance, multiples of three can be taught as skip counting by three (3, 6, 9, 12, and so on). The example provided also mentions color-coding multiples to help with pattern recognition, making it easier for students to grasp the concept.
4. What approach is suggested for teaching factors, which is noted as being a more challenging concept?
For teaching factors, the materials recommend pairing the first and the last factors of a number. This strategy aims to help pupils realize the relationships between the factors. An example provided shows the factors of 48 color-coded and paired (1x48 = 2x24 = 3x16 = 4x12 = 6x8 = 48) to illustrate this pairing concept.
5. What are some example learning goals related to factors and multiples for primary school students?
For Primary 4, learning goals include determining if a 1-digit number is a factor of a given number, listing all factors of a given number up to 100, finding common factors of two given numbers, recognizing the factor-multiple relationship, determining if a number is a multiple of a 1-digit number, listing the first 12 multiples of a 1-digit number, and finding common multiples of two given 1-digit numbers. Similar goals are outlined for Primary 5 Foundation Mathematics, with an exclusion of 'highest common factor' (H.C.F.) and 'lowest common multiple’ (L.C.M.).
6. What types of interactive resources are mentioned in connection with learning about numbers 1-100, multiples, and factors?
The resources highlight the use of JavaScript HTML5 Applet Simulation Models for interactive learning. Specifically, a model titled "Primary School Numbers from 1 to 100 only Multiples and Factors" is mentioned, which is available as an embeddable model for webpages and as downloadable apps for Android and iOS devices. These interactive tools likely allow students to explore and visualize the properties of numbers, multiples, and factors.
7. Can you provide examples of questions that might be used to assess understanding of multiples and factors within the 1-100 range?
Yes, the resources provide example questions:
- "I am a multiple of 7. I am between 50 to 100. The digit in the tens place is 0. What am I?" (Answer: 70)
- "I am a factor of 30. When you round me to the nearest tens place, you get 20. What number am I?" (Answer: 15)
- A word problem: "Miss Lim has 36 pens and 54 pencils. She distributed them equally among her students. What is the greatest number of students that Miss Lim can have?" (Answer: 18, solved by finding the greatest common factor).
8. Who are the creators and contributors associated with these learning resources on numbers 1-100?
The creators and contributors mentioned are This email address is being protected from spambots. You need JavaScript enabled to view it., Francisco Esquembre, and Felix J. Garcia Clemente. They are credited with the compilation and release of the materials under a specific license. Open Educational Resources / Open Source Physics @ Singapore is also highlighted as the platform hosting and disseminating these resources.
- Details
- Written by Loo Kang Wee
- Parent Category: Whole Numbers
- Category: 1. Numbers up to 100
- Hits: 6030








