About

Multiple Slit Diffraction

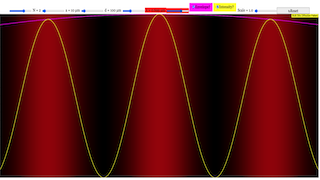
The EJS Multiple Slit Diffraction model allows the user to simulate Fraunhofer diffraction through single or multiple slits. The user can modify the number of slits, the slit width, the slit separation and the wavelength of the incident light. The scale of the diffraction pattern can also be changed and a plot of the light intensity can be toggled on and off with a checkbox.

 

The minima of single slit diffraction are determined by:

where D is the single slit width. For double slit interference, constructive interference (bright spots) are found at:

and destructive interference dark spots are located at:

where d is the distance between slits.

Multiple slits will sharpen (narrow) the regions of constructive interference.  The overall pattern from multiple slits will be the two-slit pattern multiplied by the single slit diffraction envelope.

References:

• Douglas Giancoli, Physics: Principles with Applications sixth edition, pages 664-675.
• Eugene Hecht, Optics fourth edition, pages 460-464.

Credits:

The Multiple Slit Diffraction model was created by Fu-Kwun Hwang using the Easy Java Simulations (EJS) modeling tool. It was adapted to EJS version 4.1 by Robert Mohr and Wolfgang Christian at Davidson College. You can examine and modify the model for this simulation if you have EJS installed by right-clicking within the diffraction frame and selecting "Open Ejs Model" from the pop-up menu. Information about EJS is available at: <http://www.um.es/fem/Ejs/> and in the OSP ComPADRE collection <http://www.compadre.org/OSP/>.

 

Translations

Code	Language		Translator	Run

Credits

Fu-Kwun Hwang; Robert Mohr; Wolfgang Christian; Félix J. García Clemente; Francisco Esquembre; converted to JavaScript ejss by lookang

 

Overview:

This briefing document summarizes the key information provided in the two sources regarding a JavaScript HTML5 applet simulation model for multiple slit diffraction. The applet, developed using Easy Java Simulations (EJS), allows users to explore the phenomenon of Fraunhofer diffraction through single or multiple slits by manipulating various parameters. The sources provide context on diffraction, interference, the model's functionality, underlying physics principles, and its accessibility as an open educational resource.

Main Themes and Important Ideas:

1. Fraunhofer Diffraction and Multiple Slits:

• The core topic is Fraunhofer diffraction through single and multiple slits. The simulation specifically models this type of diffraction, which occurs when the light source and the screen are far from the diffracting aperture.
• The presence of multiple slits leads to an interference pattern superimposed on the diffraction pattern produced by each individual slit.
• The simulation allows users to control key parameters affecting the diffraction pattern:
• Number of slits: Enables the observation of how increasing the number of slits alters the interference pattern.
• Slit width (D): Influences the diffraction pattern of each individual slit, determining the location of minima according to the formula provided: minima of single slit diffraction are determined by: (formula involving D).
• Slit separation (d): Determines the spacing of the interference fringes (bright and dark spots) according to the formulas provided for double-slit interference:
• Constructive interference (bright spots): constructive interference (bright spots) are found at: (formula involving d)
• Destructive interference (dark spots): destructive interference dark spots are located at: (formula involving d)
• Wavelength of incident light: Affects both the diffraction and interference patterns (spacing and position of maxima and minima).

2. Functionality of the Simulation Model:

• The "EJS Multiple Slit Diffraction model allows the user to simulate Fraunhofer diffraction through single or multiple slits."
• Users can "modify the number of slits, the slit width, the slit separation and the wavelength of the incident light."
• The model provides visual feedback by allowing users to change the "scale of the diffraction pattern."
• A crucial feature is the ability to toggle a "plot of the light intensity" on and off with a checkbox, providing a quantitative representation of the diffraction pattern.

3. Underlying Physics Principles:

• The simulation demonstrates the principles of superposition of waves. The overall diffraction pattern arises from the superposition of the waves emanating from each slit.
• For double-slit interference, the source explicitly mentions the conditions for constructive and destructive interference based on the path difference between waves from the two slits.
• For multiple slits, a key concept is that it "will sharpen (narrow) the regions of constructive interference" compared to a double-slit pattern.
• The overall intensity pattern for multiple slits is described as "the two-slit pattern multiplied by the single slit diffraction envelope." This highlights the combined effect of interference (due to multiple slits) and diffraction (due to the finite width of each slit).

4. Open Educational Resource and Accessibility:

• The model is presented as an Open Educational Resource (OER), developed by "Open Educational Resources / Open Source Physics @ Singapore."
• It is a "JavaScript HTML5 Applet Simulation Model," making it accessible through web browsers on various devices, including desktops, laptops, tablets, and smartphones (Android/iOS).
• The source provides an embed code (<iframe width="100%" height="100%" src="https://iwant2study.org/lookangejss/04waves_11superposition/ejss_model_MultipleSlitDiffraction/MultipleSlitDiffraction_Simulation.xhtml " frameborder="0"></iframe>) allowing easy integration of the simulation into webpages.
• The model was created using the Easy Java Simulations (EJS) modeling tool and adapted to JavaScript using EJS version 4.1.
• Users with EJS installed can "examine and modify the model for this simulation if you have EJS installed by right-clicking within the diffraction frame and selecting 'Open Ejs Model' from the pop-up menu." Information about EJS is available at provided URLs.
• The inclusion of "Translations" suggests efforts to make the resource accessible to a wider audience.

5. Credits and References:

• The model is credited to Fu-Kwun Hwang (creator using EJS) and adapted by Robert Mohr and Wolfgang Christian (EJS version 4.1). Further contributions include Félix J. García Clemente, Francisco Esquembre, and lookang (converted to JavaScript ejss).
• The documentation references standard physics textbooks:
• "Douglas Giancoli, Physics: Principles with Applications sixth edition"
• "Eugene Hecht, Optics fourth edition"
• These references indicate that the simulation is based on well-established physics principles and aligns with standard textbook treatments of the topic.

6. Sample Learning Goals and For Teachers:

• The presence of sections for "Sample Learning Goals" and "For Teachers" (though the content is "[text]" indicating it's not provided in the excerpt) suggests that the resource is designed with educational purposes in mind, likely to aid in student understanding of diffraction and interference.

Conclusion:

The provided sources detail a valuable open educational resource in the form of a JavaScript HTML5 applet that allows users to interactively explore the principles of multiple slit diffraction. By manipulating key parameters such as the number of slits, slit width, slit separation, and wavelength, learners can visualize the resulting diffraction patterns and intensity plots. The model is grounded in established physics principles, as evidenced by the provided formulas and textbook references. Its accessibility across various platforms and the potential for modification through EJS further enhance its utility for educational purposes. The mention of learning goals and teacher resources (even if not detailed in the excerpts) indicates a pedagogical focus in the design of this simulation.

 

Multiple Slit Diffraction Study Guide

Key Concepts

• Diffraction: The bending of waves as they pass through an opening or around an obstacle.
• Fraunhofer Diffraction: Diffraction where the light source and the screen are effectively at an infinite distance from the diffracting object, resulting in parallel incident rays.
• Single Slit Diffraction: The diffraction pattern produced when light passes through a single narrow slit, characterized by a central bright fringe and successively dimmer and narrower bright fringes (secondary maxima) separated by dark fringes (minima).
• Minima of Single Slit Diffraction: The dark fringes in a single-slit diffraction pattern, determined by the equation (D \sin \theta = m \lambda), where (D) is the slit width, (\theta) is the angle to the minimum, (m) is the order of the minimum (m = ±1, ±2, ±3,...), and (\lambda) is the wavelength of the light.
• Double Slit Interference: The interference pattern produced when light passes through two closely spaced slits, resulting in a series of bright (constructive interference) and dark (destructive interference) fringes.
• Constructive Interference (Double Slit): Bright fringes in a double-slit pattern, occurring when the path difference between the waves from the two slits is an integer multiple of the wavelength, given by (d \sin \theta = m \lambda), where (d) is the distance between the slits and (m) is the order of the maximum (m = 0, ±1, ±2, ±3,...).
• Destructive Interference (Double Slit): Dark fringes in a double-slit pattern, occurring when the path difference between the waves from the two slits is a half-integer multiple of the wavelength, given by (d \sin \theta = (m + \frac{1}{2}) \lambda), where (d) is the distance between the slits and (m) is an integer (m = 0, ±1, ±2, ±3,...).
• Multiple Slit Diffraction: The diffraction pattern produced when light passes through more than two closely spaced slits. This pattern exhibits sharper and narrower bright fringes compared to the double-slit pattern.
• Diffraction Envelope: The single-slit diffraction pattern that modulates the intensity of the multiple-slit interference pattern. The overall pattern can be thought of as the double-slit (or N-slit) interference pattern multiplied by the single-slit diffraction pattern.
• Slit Width (D): The width of each individual slit in a diffraction grating or multiple-slit setup.
• Slit Separation (d): The distance between the centers of adjacent slits in a diffraction grating or multiple-slit setup.
• Wavelength ((\lambda)): The distance between successive crests (or troughs) of a wave.
• Intensity: The power per unit area carried by a wave. In diffraction patterns, it refers to the brightness of the fringes.
• Scale of Diffraction Pattern: The size or spacing of the fringes in the diffraction pattern, which depends on the wavelength of light, the slit width, the slit separation, and the distance to the screen.
• JavaScript HTML5 Applet Simulation Model: An interactive computer program that uses JavaScript and HTML5 to visually represent and simulate the phenomenon of multiple-slit diffraction, allowing users to change parameters and observe the resulting diffraction pattern.
• Open Educational Resources (OER): Educational materials and resources offered freely and openly for anyone to use, adapt, and share.
• Open Source Physics (OSP): A project that provides computational tools and resources for physics education, often involving open-source software and simulations.
• Easy Java Simulations (EJS): A free authoring tool used to create interactive simulations, particularly in physics and other sciences. The Multiple Slit Diffraction model was originally created using EJS.

Short Answer Quiz

1. What phenomenon is the Multiple Slit Diffraction model designed to simulate? Briefly describe what happens to light waves in this phenomenon.
2. According to the provided text, what parameters can a user modify in the Multiple Slit Diffraction model? Name at least three.
3. State the equation that determines the minima in a single-slit diffraction pattern and define the variables in the equation.
4. For double-slit interference, what is the condition for constructive interference (bright spots) in terms of path difference and wavelength? Provide the relevant equation.
5. How does the interference pattern from multiple slits differ from that of a double slit with the same slit separation?
6. Explain the concept of a "diffraction envelope" in the context of multiple-slit diffraction. What determines its shape?
7. What are Fraunhofer diffraction conditions, and how are they typically approximated in experiments or simulations?
8. According to the "Credits" section, who created the original Multiple Slit Diffraction model and what software tool was used?
9. What is the role of Open Educational Resources (OER) and Open Source Physics (OSP) in the context of this simulation model?
10. How can the intensity of the light in the diffraction pattern be visualized within the simulation model described?

Answer Key for Quiz

1. The model simulates Fraunhofer diffraction through single or multiple slits. This involves the bending of light waves as they pass through the slits, followed by interference of the diffracted waves, creating a pattern of bright and dark fringes on a screen.
2. A user can modify the number of slits, the slit width, and the slit separation. The wavelength of the incident light and the scale of the diffraction pattern can also be changed.
3. The equation for minima in single-slit diffraction is (D \sin \theta = m \lambda), where (D) is the single slit width, (\theta) is the angle to the minimum, (m) is the order of the minimum (m = ±1, ±2, ±3,...), and (\lambda) is the wavelength of the light.
4. Constructive interference in a double slit occurs when the path difference is an integer multiple of the wavelength, expressed by the equation (d \sin \theta = m \lambda), where (d) is the distance between the slits and (m) is the order of the maximum (m = 0, ±1, ±2, ±3,...).
5. Multiple slits produce sharper (narrower) regions of constructive interference compared to a double slit with the same slit separation. The overall pattern retains the general spacing of the double-slit pattern but with more defined bright fringes and weaker secondary maxima.
6. The diffraction envelope is the intensity profile resulting from the single-slit diffraction of each individual slit. It modulates the intensity of the multiple-slit interference pattern, causing the overall brightness of the interference fringes to decrease as the angle from the central maximum increases. The width of the central maximum of the diffraction envelope is determined by the single-slit width (D).
7. Fraunhofer diffraction occurs when the light source and the observation screen are effectively at an infinite distance from the diffracting aperture, resulting in parallel incident and diffracted rays. This condition is often approximated by using lenses to collimate the light into parallel rays before the slits and to focus the parallel diffracted rays onto a screen.
8. The Multiple Slit Diffraction model was created by Fu-Kwun Hwang using the Easy Java Simulations (EJS) modeling tool.
9. Open Educational Resources (OER) promote free access and modification of educational materials like this simulation, allowing for wider use and adaptation. Open Source Physics (OSP) provides a platform and tools, like EJS, for creating and sharing physics simulations as OER.
10. The simulation allows the user to toggle on and off a plot of the light intensity as a function of position or angle in the diffraction pattern, providing a visual representation of the bright and dark fringes and their relative intensities.

Essay Format Questions

1. Discuss the relationship between single-slit diffraction and multiple-slit diffraction. How does the single-slit diffraction pattern influence the overall pattern observed in multiple-slit diffraction? Consider the role of slit width and slit separation in your explanation.
2. Explain how modifying the number of slits in a diffraction grating affects the resulting interference pattern. Focus on the changes in the sharpness and intensity of the principal maxima and the appearance of secondary maxima.
3. Describe the principles of wave superposition and Huygens' principle and how they contribute to the phenomena of diffraction and interference observed in multiple-slit experiments.
4. Analyze the potential pedagogical benefits of using a simulation model like the EJS Multiple Slit Diffraction model in a physics classroom. How can such a tool enhance student understanding of abstract concepts related to wave optics?
5. Compare and contrast Fraunhofer diffraction with Fresnel diffraction. Under what conditions is each type of diffraction observed, and what are the key differences in the resulting diffraction patterns?

📊

 

 

Sample Learning Goals

[text]

For Teachers

[text]

Research

[text]

Video

[text]

 Version:

1. https://weelookang.blogspot.com/2021/08/multiple-slit-diffraction-javascript.html
2. https://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=2804.msg10149#msg10149
3. https://www.compadre.org/osp/items/detail.cfm?ID=8331

Other Resources

https://www.compadre.org/osp/items/detail.cfm?ID=16739 by Wolfgang Christian using Plotly library

[text]