Breadcrumbs

Translations

Code	Language		Translator	Run

Credits

weelookang@gmail.com; Francisco Esquembre; Felix_J_Garcia_Clemente

Main Theme: The central theme is the development and availability of an interactive, open-source educational tool designed to help students, primarily at the primary and secondary levels, grasp the concepts of comparing and identifying equivalent fractions.

Key Ideas and Facts:

Title and Authorship: The simulation is attributed to "Compare Fractions" and lists the authors as weelookang@gmail.com, Francisco Esquembre, and Felix_J_Garcia_Clemente. The copyright is held by the same individuals in 2021.
Platform and Accessibility: The tool is described as an "SLS JavaScript HTML5 Applet Simulation Model," indicating it is designed to run within web browsers and potentially integrated with the Singapore Student Learning Space (SLS). The inclusion of an embed code (<iframe width="100%" height="100%" src="https://iwant2study.org/lookangejss/math/ejss_model_comparefractionsSimplev1/comparefractionsSimplev1_Simulation.xhtml " frameborder="0"></iframe>) highlights its ease of integration into online learning environments.
Open Educational Resource: The source explicitly identifies itself as part of "Open Educational Resources / Open Source Physics @ Singapore," emphasizing its commitment to freely available educational materials. The content is licensed under a "Creative Commons Attribution-Share Alike 4.0 Singapore License," promoting sharing and adaptation with attribution.
Target Audience: The categorization under "Primary," "Secondary," and "Mathematics," specifically within topics like "fractions," "Fractions of a Whole," and "Fractions Equivalent," clearly indicates the intended age groups and subject matter.
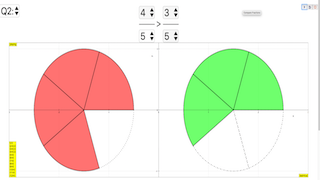
Learning Goals: The document provides explicit examples of learning goals, demonstrating the concept of equivalent fractions through equations like:
\[ \frac{1}{2} = \frac{2}{4} \http://weelookang.blogspot.sg/2017/08/comparing-fractions-javascript-html5.html") and GeoGebra applets focusing on similar concepts. This indicates a broader ecosystem of related educational materials.
Credits and Technical Foundation: The credits section acknowledges the contributions of weelookang@gmail.com, Francisco Esquembre, and Felix_J_Garcia_Clemente. The mention of "Compiled with EJS 6.1 BETA (201115)" and the link to the "Easy Java/JavaScript Simulations Toolkit" (https://www.um.es/fem/EjsWiki/) reveal the underlying technology used to develop the simulation. The license information for commercial use of the EJS library is also provided.
Integration within a Larger Platform: The presence of "Breadcrumbs" leading to "Home" and the numerous links to other educational resources within the "Open Educational Resources / Open Source Physics @ Singapore" website suggest that this fraction comparison tool is part of a larger collection of interactive learning materials. The frequent mention of "SLS" indicates a strong connection to the Singaporean educational system.
Variety of Educational Tools: The extensive list of other resources highlights the breadth of educational applets and simulations available on the platform, covering diverse subjects from physics and chemistry to mathematics and even language learning games. This context positions the fraction comparison tool within a rich environment of interactive learning resources.

Quotes:

Regarding the interactivity: "If it is Equivalent, the interactive will show the 'is equal' words."
Highlighting the open-source nature: "Contents are licensed Creative Commons Attribution-Share Alike 4.0 Singapore License."
Identifying the tool type: "Equivalent - Comparing Fractions Simple for SLS JavaScript HTML5 Applet Simulation Model"

In Conclusion:

The provided sources describe an accessible and interactive simulation designed to aid in the understanding of comparing and identifying equivalent fractions. Being an open educational resource built with JavaScript and HTML5, it can be easily integrated into various online learning platforms, including the Singapore Student Learning Space. The tool's design emphasizes hands-on exploration and immediate feedback, aligning with effective pedagogical practices for teaching mathematical concepts. Its presence within a large repository of similar educational tools further underscores its value and the broader commitment to open-source education in Singapore.

Fractions: Comparison and Equivalence Study Guide

Key Concepts

Fraction: A part of a whole, represented by a numerator (top number) and a denominator (bottom number). The denominator indicates the total number of equal parts, and the numerator indicates how many of those parts are being considered.
Numerator: The top number in a fraction, representing the number of parts being considered.
Denominator: The bottom number in a fraction, representing the total number of equal parts that make up the whole.
Equivalent Fractions: Fractions that represent the same value, even though they have different numerators and denominators. Equivalent fractions can be found by multiplying or dividing both the numerator and the denominator of a fraction by the same non-zero number.
Comparing Fractions: Determining which of two or more fractions represents a larger or smaller value. This can be done by finding a common denominator or by converting the fractions to decimals.
Common Denominator: A shared denominator that two or more fractions can use, making it easier to compare or add/subtract them. To find a common denominator, you can find the least common multiple (LCM) of the original denominators.
Simplifying Fractions: Reducing a fraction to its simplest form by dividing both the numerator and the denominator by their greatest common divisor (GCD).

Review Questions

Short Answer Quiz

Explain what a fraction represents in your own words. Provide an example of a fraction and identify its numerator and denominator.
What are equivalent fractions? Describe one method you can use to determine if two fractions are equivalent.
Why is it helpful to find a common denominator when comparing two fractions? Give a brief example.
State two different equivalent fractions for 1/2. Explain how you determined these equivalent fractions.
According to the provided materials, what will an interactive simulation show if two fractions are equivalent when explored?
Describe the relationship between the numerator and the denominator in a fraction that is equal to one whole. Provide an example.
Explain the process of simplifying a fraction. Why is it often useful to express fractions in their simplest form?
How can visual models (like those potentially found in the linked simulations) aid in understanding the concept of equivalent fractions?
Based on the titles provided, what is the primary focus of the interactive simulation described in the second source?
What are some keywords or topics listed under the "Breadcrumbs" section that relate to the concept of fractions?

Answer Key for Short Answer Quiz

A fraction represents a part of a whole or, more generally, a ratio of two quantities. For example, in the fraction 3/4, the numerator (3) represents the number of parts being considered, and the denominator (4) represents the total number of equal parts that make up the whole.
Equivalent fractions are different fractions that represent the same value. One method to determine if two fractions are equivalent is to cross-multiply. If the products of the cross-multiplication are equal, the fractions are equivalent (e.g., for a/b and c/d, if a*d = b*c, then they are equivalent).
Finding a common denominator allows for a direct comparison of the numerators, as the fractions then refer to the same size of parts of the whole. For example, to compare 1/3 and 1/4, we can use a common denominator of 12, resulting in 4/12 and 3/12, making it clear that 4/12 (or 1/3) is larger.
Two equivalent fractions for 1/2 are 2/4 and 3/6. 2/4 was determined by multiplying both the numerator and the denominator of 1/2 by 2. 3/6 was determined by multiplying both the numerator and the denominator of 1/2 by 3.
According to the "For Teachers" section, the interactive will show the words "is equal" if the fractions being compared are equivalent.
In a fraction that is equal to one whole, the numerator and the denominator are the same. For example, 4/4 represents one whole because all four parts of the whole are being considered.
Simplifying a fraction involves dividing both the numerator and the denominator by their greatest common divisor (GCD) to obtain a fraction with the smallest possible whole number numerator and denominator. This is useful because it expresses the fraction in its most concise form, making it easier to understand and compare with other fractions.
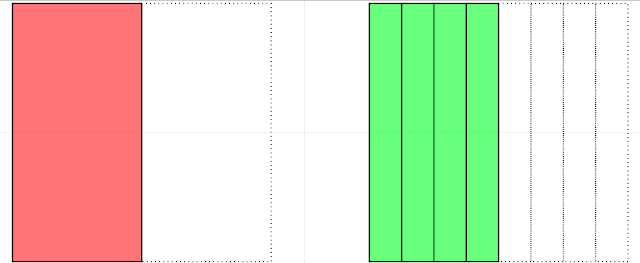
Visual models can show that different divisions of a whole can represent the same amount. For example, a circle divided into two equal halves (1/2) can be compared to a circle divided into four equal parts where two are shaded (2/4), visually demonstrating their equivalence.
The primary focus of the interactive simulation described in the second source is on understanding and exploring equivalent fractions.
The keywords or topics listed under the "Breadcrumbs" section that relate to the concept of fractions include "Mathematics," "fractions," "Fractions of a Whole," and "Fractions Equivalent."

Essay Format Questions

Discuss the importance of understanding equivalent fractions as a foundational concept for more advanced topics in mathematics. Provide examples of how this understanding might be applied in areas beyond basic fraction comparison.
Explain how interactive simulations, like the one described in the sources, can be a valuable tool for students learning about comparing and understanding equivalent fractions. What are the advantages of this type of learning over traditional methods?
Describe different strategies that can be used to compare two or more fractions. Explain the underlying mathematical principles for at least two of these strategies, and discuss when each strategy might be most appropriate to use.
Analyze the relationship between the concepts of equivalent fractions and simplifying fractions. How does understanding one concept contribute to a better understanding of the other? Provide examples to illustrate your points.
Based on the information provided, outline a potential lesson plan for introducing the concept of equivalent fractions to students using the described interactive simulation. What learning goals would you set, and how would you integrate the simulation into your lesson?

Glossary of Key Terms

Fraction: A numerical quantity that is not a whole number (e.g., 1/2, 3/4). It represents a part of a whole or, more generally, a ratio.
Numerator: The top number of a fraction, indicating the number of parts of the whole being considered.
Denominator: The bottom number of a fraction, indicating the total number of equal parts into which the whole is divided.
Equivalent Fractions: Two or more fractions that have different numerators and denominators but represent the same value (e.g., 1/2 and 2/4).
Comparing Fractions: The process of determining which of two or more fractions has a greater or lesser value.
Common Denominator: A denominator that is the same for two or more fractions, allowing for easier comparison or addition/subtraction.
Least Common Multiple (LCM): The smallest positive integer that is a multiple of two or more given integers; often used to find a common denominator.
Simplifying Fractions: Reducing a fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD).
Greatest Common Divisor (GCD): The largest positive integer that divides two or more integers without leaving a remainder; used in simplifying fractions.

Sample Learning Goals

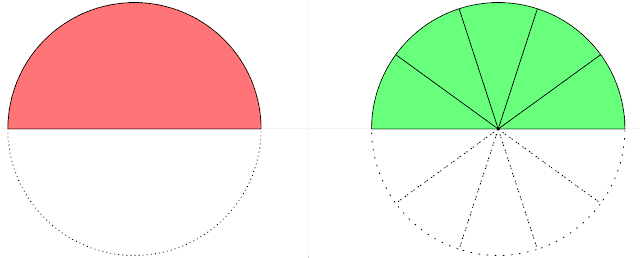
$\frac{1}{2} = \frac{2}{4}$

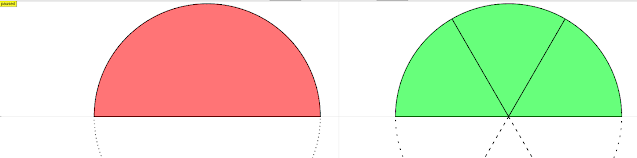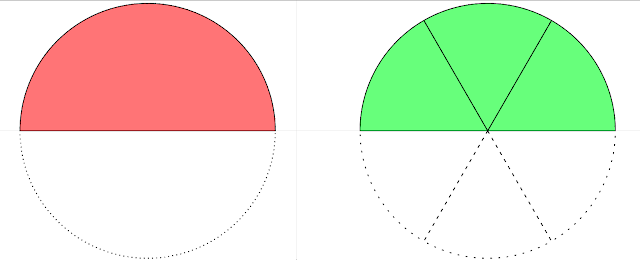$\frac{1}{2} = \frac{3}{6}$

$\frac{1}{2} = \frac{4}{8}$

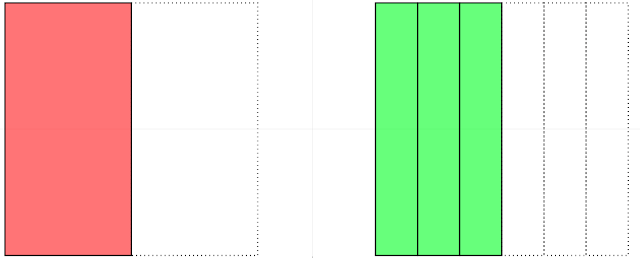
$\frac{1}{2} = \frac{5}{10}$

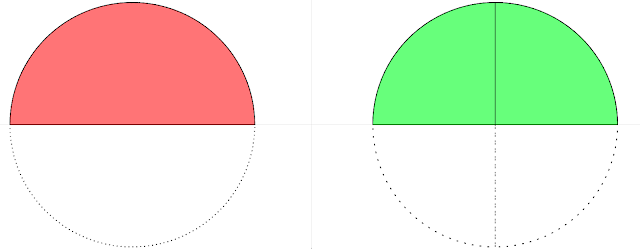
$\frac{1}{2} = \frac{3}{6}$

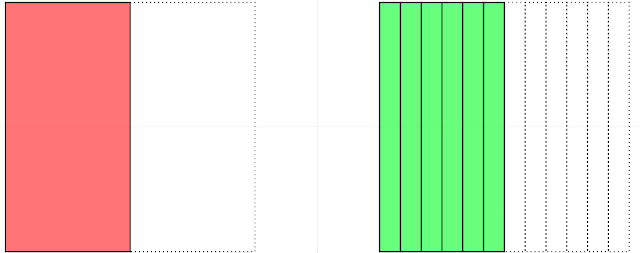
$\frac{1}{2} = \frac{2}{4}$

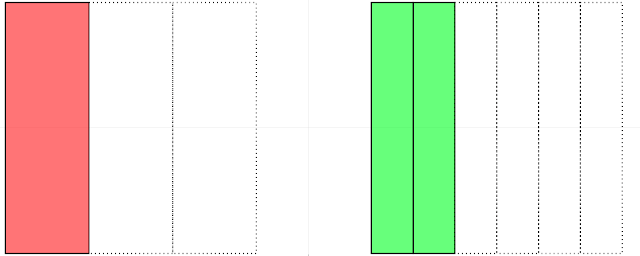
$\frac{1}{2} = \frac{6}{12}$

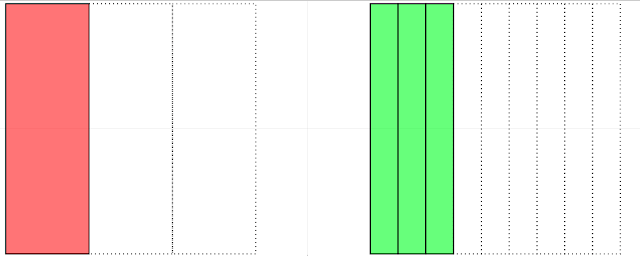
$\frac{1}{3} = \frac{3}{9}$

$\frac{1}{3} = \frac{2}{6}$

$\frac{1}{3} = \frac{3}{9}$

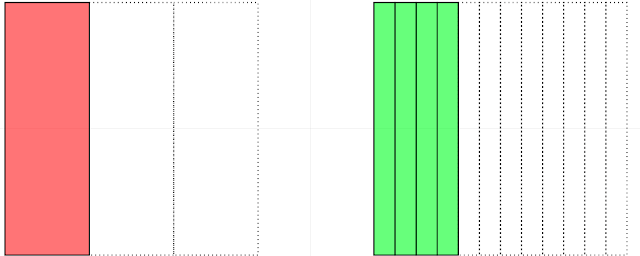$\frac{1}{3} = \frac{4}{12}$

For Teachers

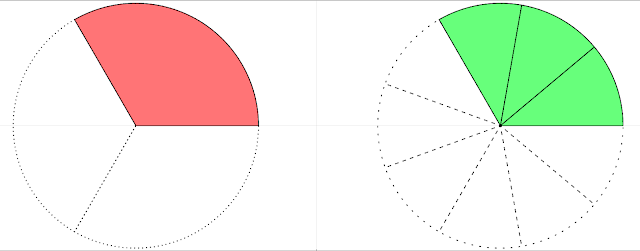
Explore this Equivalent Fractions interactive by changing the combo box on the left or directly change the denominator first. If it is Equivalent, the interactive will show the "is equal" words.

Research

[text]

Video

Version:

Other Resources

https://www.geogebra.org/m/wpzky6du

https://www.geogebra.org/m/qwjhd8kx by Lew w s

https://www.geogebra.org/m/nkj76TKW used in https://vle.learning.moe.edu.sg/mrv/community-gallery/lesson/view/a3b21ca8-6944-4437-bf53-7f6c0f730cca/page/46662849

Frequently Asked Questions about Comparing and Equivalent Fractions

1. What is the main topic addressed by these resources?

These resources primarily focus on the concept of comparing and understanding equivalent fractions. They provide interactive tools and simulations designed to help learners visualize and grasp these fundamental mathematical ideas.

2. What are equivalent fractions, and why is it important to understand them?

Equivalent fractions are different fractions that represent the same value. For example, 1/2, 2/4, and 3/6 are equivalent fractions. Understanding equivalent fractions is crucial because it allows us to simplify fractions, compare fractions with different denominators, and perform various arithmetic operations involving fractions more easily.

3. How do these resources help in understanding equivalent fractions?

These resources offer interactive simulations and applets where users can manipulate fractions, such as changing the numerator and denominator, and observe how these changes affect the fraction's value. They visually demonstrate when two fractions are equivalent by showing that they represent the same portion of a whole. For instance, the "Equivalent - Comparing Fractions Simple" tool explicitly shows "is equal" when equivalent fractions are displayed.

4. What are some of the learning goals associated with these resources?

The sample learning goals explicitly mention understanding that 1/2 is equivalent to 2/4, 3/6, 4/8, and 5/10, and that 1/3 is equivalent to 3/9, 2/6, and 4/12. These examples highlight the objective of helping learners recognize and generate equivalent fractions.

5. How can teachers use these resources in their lessons?

Teachers can embed the provided interactive models into their web pages or learning management systems. They can use these tools to visually demonstrate the concept of equivalent fractions, allow students to explore the relationship between numerators and denominators, and provide hands-on practice in identifying and creating equivalent fractions. The "For Teachers" section suggests exploring the interactive by changing the combo box or directly modifying the denominator to see when fractions are equivalent.

6. Are these resources freely available? What are the licensing terms?

Yes, these resources are generally available as Open Educational Resources under a Creative Commons Attribution-Share Alike 4.0 Singapore License. This license allows for the sharing and adaptation of the materials, provided that proper attribution is given and any derivative works are shared under the same license. However, for commercial use of the EasyJavaScriptSimulations Library, a separate license needs to be obtained from fem@um.es.

7. What kind of technology is used to deliver these interactive tools?

These resources utilize JavaScript and HTML5 to create interactive applets and simulations. This technology allows them to be run directly in web browsers without the need for additional plugins, making them accessible across various devices, including computers and tablets.

8. Besides equivalent fractions, what broader mathematical topic do these resources touch upon?

While the primary focus is on equivalent fractions, the underlying theme is the comparison of fractions. Understanding equivalence is a fundamental step in being able to compare fractions effectively, especially when they have different denominators. The title "Compare Fractions" and the functionality of showing when fractions "is equal" directly address this broader concept.

5 1 1 1 1 1 1 1 1 1 1 Rating 5.00 (1 Vote)

Details: Written by Loo Kang Wee; Parent Category: Fractions; Category: 1. Fractions of a Whole; Published: 30 August 2017; Created: 30 August 2017; Last Updated: 05 April 2025; Hits: 3772