About

Chapter 2: Round and Round the Merry-Go-Round - The Beauty That Emerges From Rotations

In the previous chapter, the judge was tasked to look at some of the foreign visitors to determine the extent of their reflection symmetry.

What he has found, to his dismay, is that each and every one of them are at least more symmetrical than the vain queen. How so? Well, the queen, being human-shaped, has only one line of symmetry. But some of the mysterious visitors have as many as eight or twelve lines of symmetry!

While he ponders on the possible ways that he can deliver this news to the queen without being locked in the dungeons for life, the arrival of a second entourage of the mysterious beings was announced. They too were summoned by the queen for judgement.

Internally resigning himself to his fate, the judge turned to look at the next wave of beings here to be checked. Expecting yet another round of crushing despair at the perfect reflection symmetries of the strange beings, he was rather surprised by what fell upon his eyes.

While a few of them did have reflection symmetry as expected, his checks revealed that some of them had no reflection symmetry whatsoever. However, what should be a happy revelation turned into puzzling stares at the strange beings. Sure, some of them weren't symmetrical in the mirror, but they had some sort of... otherworldly beauty. So much so that it made the judge tilt his head in confusion.

And then it clicked.

                                                                                                                                                                                                                                                                       

In the following simulation, we explore another form of symmetry, called rotational symmetry. Similar to reflection symmetry, instead of an object looking the same under a mirror reflection, this symmetry is the property of an object looking the same under some rotation. Even though they are both symmetries, there are some main differences between reflection and rotational symmetry.

The first notable difference is that there is no concept of a "line of symmetry" in rotational symmetry. After all, a line of symmetry tells us where to reflect the object in order to see the symmetry, but there is no reflection in rotational symmetry.

The second difference is that instead of lines of symmetry, rotational symmetry has a different concept that reflection symmetry does not have. This concept is called the order of a rotational symmetry. More informally, the order of a rotational symmetry is the number of rotational symmetries that a shape has.

We can illustrate this by looking at a simple example - that of an equilateral triangle. To make it easier for us to count, we can mark one corner of the triangle with a point, like so:

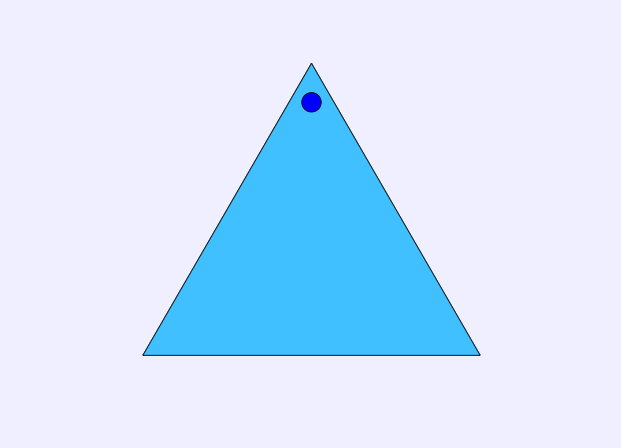
Now, how can we rotate the triangle so that it will still look the same (pretend the point isn't there, it's just to help us count)? Well, one way is to rotate the triangle 120° to the left to obtain this triangle:

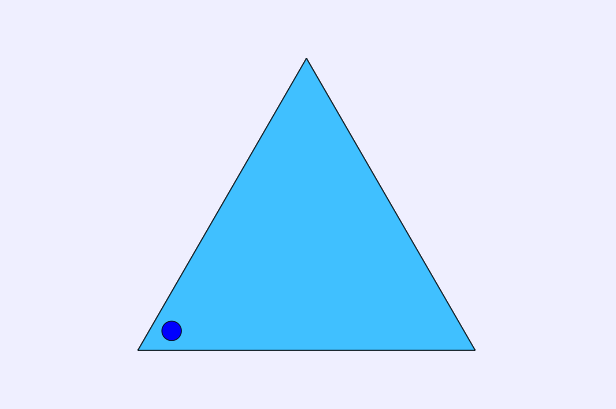
If we rotate another 120° in the same direction, this will give us yet another triangle different from the first two, as follows:

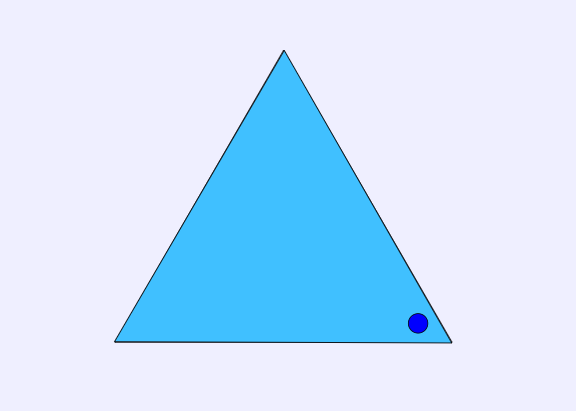
Observe that if we rotate yet another 120° in the same anti-clockwise direction, we end up back where we started, with the very first triangle above. Since we rotated the triangle 3 times, we say that the order of rotational symmetry for the equilateral triangle is 3.

In a nutshell, the order of rotational symmetry of a shape is the number of times you need to rotate the shape by a fixed nonzero angle (while keeping the shape looking the same at every step) to get back your original shape.

If you play around with shapes exhibiting rotation symmetry long enough, you may realize that there are some shapes where you can rotate a shape in multiple ways, and end up with different orders. For example, a regular hexagon (6-sided regular polygon) can be rotated in such a way that you get orders 2, 3 and 6. This is a feature, not a bug, and we shall address that later. In any case, if you end up with multiple values for the order, you should take the biggest one (more on this in a later chapter).

A special case would be if a shape has order 1. In other words, the only rotation that leaves the shape unchanged is the "do nothing" rotation. We say that the shape has no rotational symmetry in this case. We will see some of these in the simulation.

Remember, there is no rush to check all of the mysterious beings. The queen can wait for as long as you need. Have fun!

Translations

Code	Language		Translator	Run

Credits

Author name; Wei Chiong Tan

Source 1:

• Title: Not explicitly stated in the excerpt.
• Author: Wei Chiong Tan
• Copyright: © 2021, Author name; Wei Chiong Tan.
• Compilation: Compiled with EJS 6.0 (191124).
• License: Released under a license (specific license details not provided in this excerpt).

Summary of Source 1:

This source appears to be a work authored by Wei Chiong Tan, likely a digital document or application created using Easy Java/JavaScript Simulations (EJS) version 6.0. It was copyrighted in 2021 and is distributed under an unspecified license. Without further context, the specific topic or content of this source remains unknown.

Source 2:

• Title: Chapter 2: Round and Round the Merry-Go-Round - The Beauty That Emerges From Rotations Rotational Symmetry JavaScript Simulation Applet HTML5
• Source: Part of "Open Educational Resources / Open Source Physics @ Singapore"
• Author: Wei Chiong Tan (credited under "Credits")
• Publication Context: This is Chapter 2 of an epub titled "Round and Round the Merry-Go-Round - The Beauty That Emerges From Rotations." It is accessible through the "Open Educational Resources / Open Source Physics @ Singapore" platform.
• Format: The chapter includes an embeddable HTML5 JavaScript simulation applet demonstrating rotational symmetry.

Main Themes and Important Ideas:

This source focuses on introducing and explaining the concept of rotational symmetry, contrasting it with the previously discussed reflection symmetry. The narrative approach uses a judge encountering various "mysterious beings" to introduce the idea that objects can possess beauty and symmetry beyond just reflection.

Key Concepts Explained:

• Rotational Symmetry Defined: "Instead of an object looking the same under a mirror reflection, this symmetry is the property of an object looking the same under some rotation."
• Difference from Reflection Symmetry:No "line of symmetry" exists in rotational symmetry.
• Rotational symmetry introduces the concept of "order."
• Order of Rotational Symmetry: "More informally, the order of a rotational symmetry is the number of rotational symmetries that a shape has." It is further defined as "the number of times you need to rotate the shape by a fixed nonzero angle (while keeping the shape looking the same at every step) to get back your original shape."
• Illustration with Equilateral Triangle: A detailed example of an equilateral triangle with a marked corner is used to demonstrate that rotating it by 120° three times returns it to its original orientation, thus having an order of rotational symmetry of 3.
• Multiple Orders: The source notes that some shapes, like a regular hexagon, can have multiple rotational symmetries with different orders. It indicates that the largest order is typically considered.
• No Rotational Symmetry (Order 1): A shape with order 1 is defined as having "no rotational symmetry," where only a "do nothing" rotation leaves the shape unchanged.
• Interactive Learning: The text explicitly mentions an accompanying simulation ("In the following simulation...") intended to help users explore rotational symmetry. The embed code for this simulation is provided: <iframe width="100%" height="100%" src="https://iwant2study.org/lookangejss/math/ejss_model_Rotation_Symmetry/Rotation_Symmetry_Simulation.xhtml " frameborder="0"></iframe>
• Emphasis on Exploration: The concluding remarks encourage the reader to "play around with shapes" and to take their time, reinforcing the educational and exploratory nature of the resource.

Additional Information:

• The source is part of a larger work or platform focused on Open Educational Resources in Physics from Singapore.
• It is located within a section titled "Boost Your Math Proficiency: Explore designating the floors, inspired by an Interactive Math Textbook (Work-In-Progress)." This suggests a connection to mathematics education.
• The chapter is available as part of an epub.
• Credits are given to Wei Chiong Tan as the author.
• The page includes a significant number of links to other interactive simulations and resources, indicating a broader collection of educational materials.
• The platform utilizes a Creative Commons Attribution-Share Alike 4.0 Singapore License for its content, with a separate license for commercial use of the EasyJavaScriptSimulations Library.

Overall Significance:

The excerpt from "Chapter 2: Round and Round the Merry-Go-Round" provides a clear and engaging introduction to the concept of rotational symmetry. It effectively distinguishes it from reflection symmetry and uses a concrete example to explain the "order" of rotational symmetry. The inclusion of a JavaScript simulation applet highlights the interactive and practical approach to learning this mathematical concept within the "Open Educational Resources / Open Source Physics @ Singapore" platform. The presence of numerous other educational resources on the same page suggests a rich environment for exploring various scientific and mathematical topics.

Rotational Symmetry Study Guide

Key Concepts:

• Symmetry: A property of an object where it remains unchanged under certain transformations.
• Rotational Symmetry: A type of symmetry where an object looks the same after being rotated by a specific angle around a central point.
• Line Symmetry (Reflection Symmetry): A type of symmetry where an object can be divided into two identical halves by a line of symmetry, acting like a mirror.
• Rotation: The act of turning an object around a fixed point.
• Order of Rotational Symmetry: The number of distinct rotational symmetries a shape has within a full 360-degree rotation (including the "do nothing" rotation only once in the count of transformations that leave the shape unchanged). It is the number of times the shape looks identical to its original orientation as it is rotated 360 degrees.
• No Rotational Symmetry: A shape has no rotational symmetry if the only rotation that leaves it unchanged is a 360-degree (or 0-degree) rotation (order 1).

Quiz:

1. What is the fundamental difference between rotational symmetry and reflection symmetry as described in the text?
2. Explain the concept of the "order" of rotational symmetry using the example of the equilateral triangle provided in the text.
3. According to the text, can a shape possess both rotational symmetry and reflection symmetry? Provide a brief explanation.
4. What does it mean if a shape has an order of rotational symmetry equal to 1? Give an example (not explicitly mentioned in the text, but logically consistent).
5. The text mentions that a regular hexagon can have rotational symmetries of order 2, 3, and 6. In such a case, which order is typically considered the "biggest" one, and why might this be significant?
6. In the judge's initial assessment, what type of symmetry did the foreign visitors primarily exhibit, causing him dismay?
7. What was the judge's surprising observation about the second group of mysterious beings that led him to consider rotational symmetry?
8. Does rotational symmetry involve a "line of symmetry"? Explain your answer based on the provided text.
9. Summarize the author's main point about rotational symmetry in comparison to the queen's symmetry.
10. What is the practical way suggested in the text to determine the order of rotational symmetry of a shape?

Answer Key:

1. The main difference is that reflection symmetry involves an object looking the same under a mirror reflection across a line of symmetry, while rotational symmetry involves an object looking the same after being rotated around a central point by a specific angle, without any reflection.
2. The order of rotational symmetry is the number of times a shape looks identical to its original orientation during a full 360-degree rotation. For an equilateral triangle, rotating it 120°, then another 120°, and finally another 120° (back to the start) results in the same appearance three times, thus its order of rotational symmetry is 3.
3. Yes, a shape can possess both rotational and reflection symmetry. The text implies this when mentioning that while some of the second group of beings had no reflection symmetry, others did, and the focus shifted to rotational symmetry as another form of symmetry.
4. If a shape has an order of rotational symmetry of 1, it means that the only rotation that leaves the shape unchanged is a 360-degree (or 0-degree) rotation. Such a shape has no rotational symmetry in a meaningful sense; an example would be a scalene triangle.
5. The biggest order (in this case, 6 for the regular hexagon) is typically considered. This is likely because it encompasses all the possible rotational symmetries of the shape. The text hints that this will be addressed in a later chapter.
6. The foreign visitors initially exhibited reflection symmetry, with some having as many as eight or twelve lines of symmetry, which was far more than the queen's single line of symmetry.
7. The judge observed that while some of the second group had reflection symmetry, others had none. However, these non-reflection-symmetrical beings possessed a different kind of beauty, which he realized was due to rotational symmetry.
8. No, rotational symmetry does not involve a "line of symmetry." The text explicitly states that there is no concept of a "line of symmetry" in rotational symmetry because it deals with rotation, not reflection.
9. The author highlights that rotational symmetry is another form of symmetry that some objects possess, and that some beings can be more symmetrical than the queen in terms of the type of symmetry they exhibit (rotational versus reflection) or the degree of reflectional symmetry.
10. The practical way suggested is to rotate the shape by a fixed nonzero angle repeatedly and count how many times it looks the same as the original shape before returning to the starting position after a full 360-degree rotation.

Essay Format Questions:

1. Compare and contrast reflectional symmetry and rotational symmetry, drawing upon the examples and explanations provided in the text. How does the concept of "order" uniquely define rotational symmetry?
2. Discuss the significance of the judge's shift in perspective from reflectional symmetry to rotational symmetry. What does this transition reveal about the different ways in which objects can exhibit symmetry and beauty?
3. Explain the concept of the "order of rotational symmetry" in detail. Use hypothetical examples (beyond the equilateral triangle) to illustrate different orders of rotational symmetry and the implications of a shape having a higher or lower order.
4. Analyze the author's use of the narrative involving the judge and the mysterious beings. How effective is this approach in introducing and explaining the concept of rotational symmetry? What are the advantages of this narrative style?
5. Based on the text, how can the exploration of symmetry, both reflectional and rotational, enhance our understanding and appreciation of the natural and constructed world around us? Provide examples of objects or patterns that exhibit these types of symmetry.

Glossary of Key Terms:

• Symmetry: The quality of being made up of exactly similar parts facing each other or around an axis. In mathematics, it refers to a transformation that leaves an object unchanged.
• Rotational Symmetry: The property of a shape that looks the same after being rotated by a certain angle around a central point.
• Line Symmetry (Reflection Symmetry): The property of a shape that can be divided into two identical halves by a line of symmetry, such that one half is a mirror image of the other.
• Rotation: The act of moving an object in a circular path around a center.
• Order of Rotational Symmetry: The number of times a shape looks exactly the same as its original orientation during a full 360-degree rotation.
• Transformation: An operation that changes the position, shape, or size of a geometric figure. Rotation and reflection are examples of transformations.

Sample Learning Goals

[text]

For Teachers

[text]

Research

[text]

Video

[text]

 Version:

1. http://weelookang.blogspot.sg/2016/02/vector-addition-b-c-model-with.html improved version with joseph chua's inputs
2. http://weelookang.blogspot.sg/2014/10/vector-addition-model.html original simulation by lookang

Other Resources

[text]