About
Brownian motion
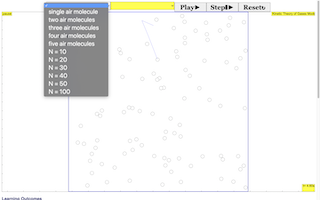
This is a simulation of brownian motion of a particle that collides with a large set of smaller particles which move with uniform motion in different random directions.
For more info:
http://weelookang.blogspot.sg/2010/06/ejs-open-source-brownian-motion-gas.html
Original Author:
Simulación preparada por Francisco Esquembre para el libro
Creación de Simulaciones Interactivas en Java.
Aplicación
a la Enseñanza de la Física
(C) Pearson Educación 2004.
Modified by Fu-Kwun Hwang
http://www.phy.ntnu.edu.tw/ntnujava/
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits
Francisco Esquembre; Fu-Kwun Hwang; lookang
{accordionfaq faqid=accordion3 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}
Introduction
Brownian motion or pedesis (from Ancient Greek: πήδησις/pέːdεːsis/ "leaping") is the random motion of particles suspended in a fluid (a liquid or a gas) resulting from their collision with the fast-moving atoms or molecules in the gas or liquid.[1] This transport phenomenon is named after the botanist Robert Brown. In 1827, while looking through a microscope at particles trapped in cavities inside pollen grains in water, he noted that the particles moved through the water. Atoms and molecules had long been theorized as the constituents of matter, and Albert Einstein published a paper in 1905 that explained in precise detail how the motion that Brown had observed was a result of the pollen being moved by individual water molecules. This explanation of Brownian motion served as convincing evidence that atoms and molecules exist, and was further verified experimentally by Jean Perrin in 1908. Perrin was awarded the Nobel Prize in Physics in 1926 "for his work on the discontinuous structure of matter" (Einstein had received the award five years earlier "for his services to theoretical physics" with specific citation of different research). The direction of the force of atomic bombardment is constantly changing, and at different times the particle is hit more on one side than another, leading to the seemingly random nature of the motion.
Brownian motion is among the simplest of the continuous-time stochastic (or probabilistic) processes, a big idea in physics.
Other Resources
http://mw.concord.org/nextgen/interactives/
surprisingly similiar random movement between brownian and diffusion.
Add a drop of dye anywhere in the container, and watch it diffuse through the water.
Click in the model to add a drop of dye. Watch how the molecules move through the water. Trace an individual molecule to see how it moves through the liquid.
http://lab.concord.org/embeddable.html#interactives/sam/diffusion/1-dropping-dye-on-click.json
How does temperature affect the rate of diffusion?
Explore the role of temperature on the rate of diffusion. Set the temperature, then remove the barrier, and measure the amount of time it takes the blue molecules to reach the gas sensor. When the gas sensor has detected three blue molecules, it will stop the experiment. Compare the diffusion rates at low, medium and high temperatures. Trace an individual molecule to see the path it takes.
http://lab.concord.org/embeddable.html#interactives/sam/diffusion/2-temperature.json
How does molecular mass affect the rate of diffusion?
Explore the role of molecular mass on the rate of diffusion. Select the mass of the molecules behind the barrier. Remove the barrier, and measure the amount of time it takes the molecules to reach the gas sensor. When the gas sensor has detected three molecules, it will stop the experiment. Compare the diffusion rates of the lightest, heavier and heaviest molecules. Trace an individual molecule to see the path it takes.
http://lab.concord.org/embeddable.html#interactives/sam/diffusion/3-mass.json
How does pore size affect the diffusion of different molecules?
Biological membranes are selectively permeable; some molecules can cross while others cannot. One way to affect this is through pore size. Change the pore size with the slider to change the permeability of the membrane to the different types of molecules. Trace an individual molecule to see the path it takes.
Cell membranes are composed of two layers of phospholipids (a phospholipid bilayer). Some molecules are capable of crossing this membrane directly, without use of specific membrane channels.
Oxygen and carbon dioxide are two molecules that can freely cross the cell membrane. In aerobic cells, oxygen is necessary for cell functioning and carbon dioxide is produced as a waste molecule. Hence, the cell “wants” oxygen to enter and carbon dioxide to leave. But molecules don’t move only in one direction–they diffuse randomly across the membrane.
Set up the model with high oxygen and low carbon dioxide outside the cell and low oxygen and high carbon dioxide inside the cell. In which direction do the oxygen and carbon dioxide molecules move?
http://lab.concord.org/embeddable.html#interactives/sam/diffusion/5-permeable-membrane.json
How does pore size affect the diffusion of different molecules?
Biological membranes are selectively permeable; some molecules can cross while others cannot. One way to affect this is through pore size. Change the pore size with the slider to change the permeability of the membranes to the different types of molecules. Trace an individual molecule to see the path it takes.
Video
https://www.youtube.com/watch?v=gPMVaAnij88 by STEM Learning
Versions:
Other resources
http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=1121.0 simplied flu spreading model by Fu-Kwun Hwang
end faq
{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}
- Details
- Parent Category: 12 Temperature & Ideal Gases
- Category: 01 Kinetic Model
- Hits: 3703