.png
)
About
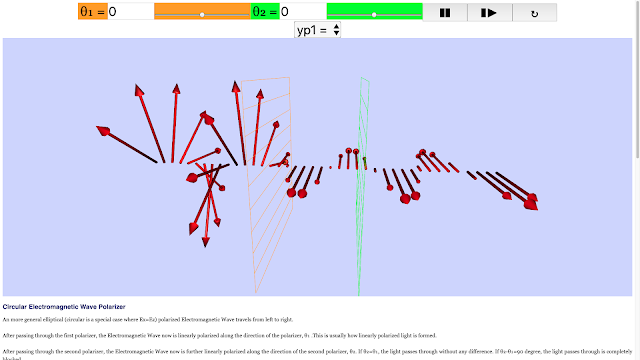
Circular Electromagnetic Wave Polarizer
An more general elliptical (circular is a special case where Ex=Ez) polarized Electromagnetic Wave travels from left to right.
After passing through the first polarizer, the Electromagnetic Wave now is linearly polarized along the direction of the polarizer, θ₁ .This is usually how linearly polarized light is formed.
After passing through the second polarizer, the Electromagnetic Wave now is further linearly polarized along the direction of the second polarizer, θ₂. If θ₂=θ₁, the light passes through without any difference. If θ₂-θ₁=90 degree, the light passes through is completely blocked.
After passing through the third polarizer,the Electromagnetic Wave now is further linearly polarized along the direction of the third polarizer, θ₃. If θ₃ = θ₂= θ₁,the linearly polarized light passes through without any difference. If θ₃-θ₂=90 degree and θ₂-θ₁=0 degree, light inbetween polarizer 2 and 3 is unchanged, still linearly polarized, but light after polarizer 3 is completely blocked.
Visualization
Electric Field is represented as Red color segments
Magnetic Field is represented as Blue color segments
Polarizer 1 is Orange color
Polarizer 2 is Green color
Polarizer 3 is Magenta color
Controls
You can modify:
θ₁ is the angle of the first polarizer
θ₂ is the angle of the second polarizer
θ₃ is the angle of the third polarizer
under the combobox
yp₁ is the position of the first polarizer
yp₂ is the position of the second polarizer
yp₃ is the position of the third polarizer
under more? it is possible to explore these other more advance variables
Ex: electric field magnitude in x direction
Ez: electric field magnitude in z direction
phase: the phase difference between E and B
vy: wave velocity. which imply Ez/Bx=vy, where Bx is magnetic field magnitude
T :period of the wave. which imply wavelength(lamda)=vy*T
wavelength: the length of one cycle of the wave
Please notice that E/B field are in phase when electromagnetic is travel in vacuum.
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits
Fremont Teng; Fu-Kwun Hwang; lookang
For Teachers
Circular Electromagnetic Wave Polarizer JavaScript Simulation Applet HTML 5
 |
| A more general elliptical (circular is a special case where Ex=Ez) polarized Electromagnetic Wave travels from left to right. After passing through the first polarizer, the Electromagnetic Wave now is linearly polarized along the direction of the polarizer, θ₁ .This is usually how linearly polarized light is formed.After passing through the second polarizer, the Electromagnetic Wave now is further linearly polarized along the direction of the second polarizer, θ₂. If θ₂=θ₁, the light passes through without any difference |
 |
| A more general elliptical (circular is a special case where Ex=Ez) polarized Electromagnetic Wave travels from left to right. After passing through the first polarizer, the Electromagnetic Wave now is linearly polarized along the direction of the polarizer, θ₁ .This is usually how linearly polarized light is formed.After passing through the second polarizer, the Electromagnetic Wave now is further linearly polarized along the direction of the second polarizer, θ₂. If θ₂-θ₁=90 degree, the light passes through is completely blocked. |
Circular Electromagnetic Wave Polarizer
A more general elliptical (circular is a special case where Ex=Ez) polarized Electromagnetic Wave travels from left to right.
After passing through the first polarizer, the Electromagnetic Wave now is linearly polarized along the direction of the polarizer, θ₁ .This is usually how linearly polarized light is formed.
After passing through the second polarizer, the Electromagnetic Wave now is further linearly polarized along the direction of the second polarizer, θ₂. If θ₂=θ₁, the light passes through without any difference. If θ₂-θ₁=90 degree, the light passes through is completely blocked.
Visualization
Electric Field is represented as Red color segments
Magnetic Field is represented as Blue color segments
Polarizer 1 is Orange color
Polarizer 2 is Green color
Controls
You can modify:
θ₁ is the angle of the first polarizer
θ₂ is the angle of the second polarizer
under the combobox
yp₁ is the position of the first polarizer
yp₂ is the position of the second polarizer
under more? it is possible to explore these other more advance variables
Ex: electric field magnitude in x direction
Ez: electric field magnitude in z direction
phase: the phase difference between E and B
vy: wave velocity. which imply Ez/Bx=vy, where Bx is magnetic field magnitude
T :period of the wave. which imply wavelength(lamda)=vy*T
Please notice that E/B field are in phase when electromagnetic is travel in vacuum.
Instructions on using Simulation Applet
Combo Boxes
Play, Pause and Reset Buttons
Version:
- http://weelookang.blogspot.com/2018/02/circular-electromagnetic-wave-polarizer.html
- https://weelookang.blogspot.com/2020/03/circular-electromagnetic-wave-2.html
Video
https://www.youtube.com/watch?v=ZXZOLscuyE8 by xmtutor
Other Resources
end faq
{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}