Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.; Cleve Chia
Introduction:
This briefing document summarizes the key themes and information presented in two related open educational resources focusing on the "Angle of Release Projectile Motion Model for Exercise Sports Science." These resources, developed by This email address is being protected from spambots. You need JavaScript enabled to view it. and Cleve Chia under a Creative Commons Attribution license, provide a model and simulation tool to understand how the angle at which a projectile is released affects its motion, specifically in the context of sports science. The materials emphasize the importance of understanding these principles for optimizing performance in various sporting activities.
2. Main Themes and Important Ideas:
The central theme of these resources is the relationship between the angle of release of a projectile and its subsequent trajectory, including maximum height, maximum distance (range), and flight time. The resources utilize a JavaScript HTML5 applet simulation model to visually demonstrate these relationships and provide concrete data points.
Key Concepts and Ideas:
- Projectile Motion: The fundamental concept explored is projectile motion, defined as the motion of an object acted upon by gravity once released into the air. The description explicitly mentions examples relevant to sports, such as "a shot put, a javelin, a human body during pole-vaulting."
- Quote: "Projectile motion refers to the motion of a projected object (e.g., a shot put, a javelin, a human body during pole-vaulting) acted on by forces of gravity."
- Negligible Air Resistance (Simplification): The model simplifies the physics by considering air resistance to be negligible. This allows for a more straightforward understanding of the core principles related to the angle of release.
- Quote: "For simplicity, air resistance is considered negligible in the following cases."
- Importance in Sports: The resources highlight the practical significance of understanding projectile motion in sports, emphasizing that once an object (or athlete in some cases) is released, its trajectory is predetermined by the initial conditions, including the angle of release.
- Quote: "In sports, once the projected object is released or thrown in the air, control of the object is no longer possible. Therefore, it is important to consider the following factors that affect the flight path of the projectile prior to its release:"
- Definition of Angle of Release: The angle of release is clearly defined as the angle of projection with respect to the horizontal.
- Quote: "Angle of release refers to the angle at which the projectile is thrown with respect to the positive x axis or horizontal level to the right."
- Influence on Trajectory Shape: The angle of release directly influences the shape of the projectile's flight path.
- Quote: "The direction of projection with respect to the horizontal determines the shape of flight."
- Relationship between Angle and Maximum Height: A higher projection angle results in a greater maximum height achieved by the projectile.
- Quote: "A higher projection angle will result in a higher maximum height achieved by the projectile."
- Optimal Angle for Maximum Distance (Zero Relative Projection Height): When the launch and landing heights are the same (zero relative projection height), an angle of release close to 45 degrees is optimal for achieving the greatest horizontal distance.
- Quote: "When the relative projection height is zero, for the projectile to achieve a greater maximum distance, the projection angle should be close to 45 degrees."
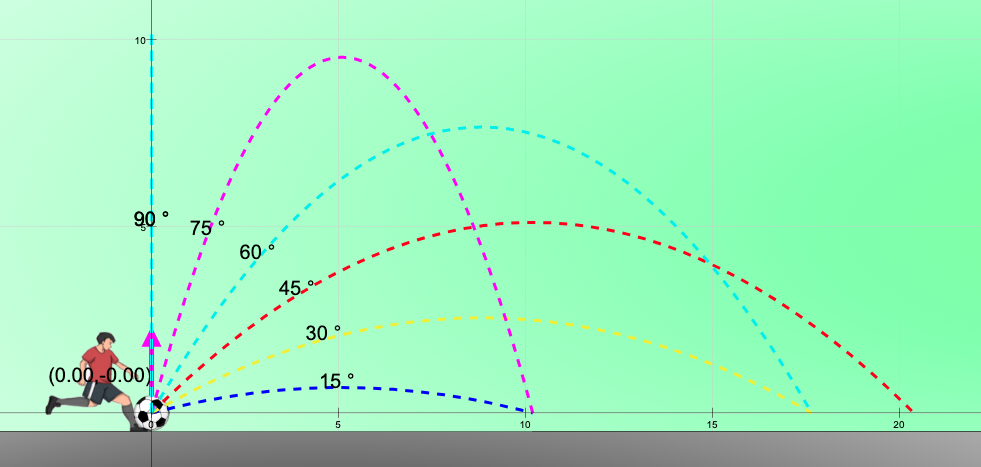
- Simulation and Data Table: The resources include a JavaScript HTML5 applet simulation model (accessible via an iframe embed) and a table demonstrating the relationship between the angle of release (from 0 to 90 degrees) and the resulting maximum height, maximum distance, and flight time. This provides empirical evidence for the principles discussed.
- | Angle of Release | Maximum Height (m) | Maximum Distance (m) | Flight Time (s) | | :---------------: | :----------------: | :-------------------: | :-------------: | | 0 | 0 | 0 | 0 | | 15 | 0.68 | 10.19 | 0.75 | | 30 | 2.55 | 17.66 | 1.44 | | 45 | 5.10 | 20.39 | 2.04 | | 60 | 7.65 | 17.66 | 2.50 | | 75 | 9.51 | 10.19 | 2.78 | | 90 | 10.19 | 0 | 2.88 |
- Visual Representation (Graphs): The simulation includes graphs that visually represent how different angles of projection affect the maximum height and distance, reinforcing the data presented in the table.
- Example Questions and Answers: The resources provide sample questions related to the concepts, along with acceptable answers, which can be valuable for educators in assessing understanding.
- Question 1: "Estimate the angle of release of the football when the range is the greatest." Answer: "acceptable answer is 45 degrees"
- Question 2: "Sam claimed that the angle of release of the football does not affected maximum time of flight of the football. Do you agree? Explain." Answer: "disagree. From the simulation, as the angle of release chnages from 0 to 90 degrees, the maximum time of flight also increases."
- Question 3: "Use the tool above, suggest whether the maximum height increase/decease/constant, as the angle of release increases." Answer: "maximum height increases"
3. Potential Applications and Educational Value:
These resources offer significant educational value for:
- Physical Education Teachers and Students: Providing a clear and interactive way to understand the physics behind sports movements involving projectiles.
- Exercise Science Professionals and Students: Demonstrating the biomechanical principles that influence athletic performance.
- Curriculum Developers: Offering open-source materials that can be integrated into physics and physical education curricula.
- Self-Learners: Providing an accessible and engaging way to learn about projectile motion.
The JavaScript simulation allows for hands-on exploration of different release angles and their impact on the trajectory, making the learning process more interactive and intuitive. The provided data and example questions further enhance understanding and facilitate assessment.
4. Technical Aspects and Credits:
The model and simulation are built using EJS 6.1 BETA (Easy JavaScript Simulations) and are released under a Creative Commons Attribution-Share Alike 4.0 Singapore License. The resources credit This email address is being protected from spambots. You need JavaScript enabled to view it. and Cleve Chia for their development. The simulation can be embedded into webpages using the provided iframe code, making it easily shareable and integrable into online learning platforms. The Open Educational Resources / Open Source Physics @ Singapore initiative provides a platform for these and many other science and physics simulations.
5. Further Exploration:
The resources encourage further exploration using the simulation model. The extensive list of "Other Resources" and "Popular Tags" on the Open Educational Resources / Open Source Physics @ Singapore website indicates a wealth of related interactive simulations and materials available for various topics in physics, mathematics, and other subjects. This broader context suggests a rich ecosystem of open educational tools that educators can leverage.
6. Conclusion:
The "Angle of Release Projectile Motion Model for Exercise Sports Science" provides a valuable and accessible resource for understanding a fundamental principle in sports biomechanics. The combination of clear explanations, a dynamic simulation, empirical data, and example questions makes it an effective tool for teaching and learning about the impact of release angle on projectile trajectory. The open-source nature and Creative Commons license further enhance its utility for educators and learners worldwide.
Angle of Release in Projectile Motion: A Study Guide
Key Concepts
- Projectile Motion: The motion of an object projected into the air, influenced primarily by gravity and (in simplified models) neglecting air resistance.
- Angle of Release: The angle at which a projectile is launched with respect to the horizontal. This angle significantly impacts the trajectory of the projectile.
- Maximum Height: The highest vertical position reached by a projectile during its flight.
- Maximum Distance (Range): The total horizontal distance traveled by a projectile before returning to its initial vertical level (or a defined landing level).
- Flight Time: The total duration a projectile remains in the air from launch to landing.
- Trajectory: The path followed by a projectile as it moves through the air.
- Gravity: The force that pulls objects towards the center of the Earth, causing a constant downward acceleration on projectiles.
- Horizontal Velocity: The component of the initial velocity in the horizontal direction. In the absence of air resistance, this velocity remains constant throughout the projectile's flight.
- Vertical Velocity: The component of the initial velocity in the vertical direction. This velocity is affected by gravity, decreasing as the projectile moves upward and increasing as it falls downward.
- Relative Projection Height: The difference in vertical height between the launch point and the landing point. The provided source focuses on cases where this is zero.
Quiz
Answer the following questions in 2-3 sentences each.
- Define projectile motion as described in the provided text.
- According to the source, what is the primary force acting on a projectile after it is released? What force is explicitly considered negligible in the simplified models discussed?
- Explain the concept of the angle of release. How is this angle typically measured?
- Based on the provided table, what angle of release results in the greatest maximum distance when the relative projection height is zero?
- Describe the relationship between the angle of release and the maximum height achieved by a projectile, as indicated by the source.
- Does the source agree with the claim that the angle of release does not affect the maximum time of flight of a projectile? Explain your reasoning based on the provided data.
- How does the shape of a projectile's flight path change as the angle of release is altered?
- What are some factors that athletes should consider prior to releasing a projectile in sports, according to the text?
- Using the information from the table, compare the maximum distances achieved with launch angles of 30 degrees and 60 degrees. What do you observe?
- Briefly explain why controlling the projectile after release is described as no longer possible in sports contexts.
Quiz Answer Key
- Projectile motion, as defined in the text, refers to the movement of an object that has been projected or thrown into the air. This motion is primarily influenced by the force of gravity acting upon the object.
- The primary force acting on a projectile after release, according to the source, is gravity. For simplicity in the cases discussed, the effect of air resistance is considered negligible.
- The angle of release is the angle at which a projectile is launched or thrown with respect to the positive horizontal axis. It determines the initial direction of the projectile's velocity vector.
- According to the provided table, an angle of release of 45 degrees results in the greatest maximum distance (20.39 m) when the relative projection height is zero.
- The source indicates a direct relationship between the angle of release and the maximum height achieved. As the angle of release increases from 0 to 90 degrees, the maximum height of the projectile also increases.
- No, the source disagrees with the claim. The provided table shows that as the angle of release increases from 0 to 90 degrees, the maximum time of flight also increases, indicating a clear effect.
- The direction of projection, determined by the angle of release, dictates the shape of the projectile's flight path. Lower angles produce flatter, longer trajectories (for range), while higher angles result in higher, shorter trajectories (for height).
- According to the text, athletes should consider factors that affect the projectile's flight path prior to release, such as the angle of release, to optimize the outcome of their throw or projection.
- The table shows that both a 30-degree and a 60-degree launch angle result in the same maximum distance of 17.66 meters. This demonstrates that complementary launch angles (adding up to 90 degrees) can yield the same horizontal range when the launch and landing heights are equal and air resistance is negligible.
- Once a projectile is released or thrown in sports, the athlete no longer has direct physical contact or control over its motion. Its trajectory is then solely determined by the initial conditions (like angle and speed of release) and the external forces acting upon it (primarily gravity).
Essay Format Questions
Consider the following questions and plan a well-structured essay response for each.
- Discuss the significance of the angle of release in various sports involving projectile motion. Provide specific examples from different sports and explain how the optimal angle of release might vary depending on the objective (e.g., maximum distance vs. maximum height).
- Explain the relationship between the angle of release, maximum height, maximum distance, and flight time of a projectile, assuming negligible air resistance and a level launch and landing surface. Support your explanation with evidence from the provided table.
- The provided text simplifies projectile motion by neglecting air resistance. In a real-world sporting scenario, how would air resistance affect the trajectory of a projectile, and how might this influence the optimal angle of release for achieving maximum distance?
- Analyze the claim that an angle of release close to 45 degrees is optimal for maximum distance when the relative projection height is zero. Discuss the assumptions underlying this statement and whether this angle would remain optimal in situations with a significant relative projection height.
- Based on the information provided and your understanding of projectile motion, discuss the key factors that a coach in a sport like javelin throwing or basketball shooting would emphasize to help athletes optimize their angle of release for success.
Glossary of Key Terms
- Projectile: An object propelled into the air and subject to the forces of gravity.
- Trajectory: The curved path followed by a projectile in flight.
- Launch Angle: Synonym for angle of release; the angle at which the projectile is initially projected.
- Range: The horizontal distance covered by a projectile from its launch point to its landing point (assuming the same vertical level).
- Apex: The highest point reached by a projectile in its trajectory, where its vertical velocity momentarily becomes zero.
- Horizontal Range: Another term for maximum distance, specifically referring to the distance traveled horizontally.
- Vertical Displacement: The change in the vertical position of the projectile during its flight.
- Initial Velocity: The velocity of the projectile at the moment of release, having both horizontal and vertical components determined by the launch speed and angle.
- Gravitational Acceleration (g): The constant acceleration experienced by objects due to gravity, approximately 9.8 m/s² downwards on Earth.
- Parabolic Path: The characteristic curved trajectory followed by a projectile under constant gravitational acceleration when air resistance is negligible.
Description
Projectile Motion
Projectile motion refers to the motion of a projected object (e.g., a shot put, a javelin, a human body during pole-vaulting) acted on by forces of gravity.
For simplicity, air resistance is considered negligible in the following cases.
In sports, once the projected object is released or thrown in the air, control of the object is no longer possible. Therefore, it is important to consider the following factors that affect the flight path of the projectile prior to its release:
b. Angle of release
Angle of release refers to the angle at which the projectile is thrown with respect to the positive x axis or horizontal level to the right. The direction of projection with respect to the horizontal determines the shape of flight. A higher projection angle will result in a higher maximum height achieved by the projectile. When the relative projection height is zero, for the projectile to achieve a greater maximum distance, the projection angle should be close to 45 degrees.
| Angle of Release | maximum height | maximum distance | flight time |
|---|---|---|---|
| 0 | 0 m | 0 m | 0 s |
| 15 | 0.68 m | 10.19 m | 0.75 s |
| 30 | 2.55 m | 17.66 m | 1.44 s |
| 45 | 5.10 m | 20.39 m | 2.04 s |
| 60 | 7.65 m | 17.66 m | 2.50 s |
| 75 | 9.51 m | 10.19 m | 2.78 s |
| 90 | 10.19 m | 0 m | 2.88 s |
More details can be explored on the simulation above
Possible Question 1. Estimate the angle of release of the football when the range is the greatest.
acceptable answer is 45 degrees
Possible Question 2. Sam claimed that the angle of release of the football does not affected maximum time of flight of the football. Do you agree? Explain.
disagree. From the simulation, as the angle of release chnages from 0 to 90 degrees, the maximum time of flight also increases.
Possible Question 3. Use the tool above, suggest whether the maximum height increase/decease/constant, as the angle of release increases.
maximum height increases
Video
[text]
Version
Other Resources
[text]
Frequently Asked Questions: Angle of Release in Projectile Motion
1. What is projectile motion, as described in these sources?
Projectile motion refers to the movement of an object that has been launched or thrown into the air (a projectile), such as a shot put, a javelin, or even a person during a pole vault. Once the object is released, the primary force acting upon it is gravity. For simplicity in the models discussed, air resistance is generally considered negligible. Importantly, after release, the projector no longer has direct control over the object's trajectory.
2. What is the "angle of release" and why is it significant in projectile motion?
The angle of release is the angle at which a projectile is launched or thrown with respect to the horizontal plane (positive x-axis). This angle is crucial because it fundamentally determines the shape of the projectile's flight path. By adjusting the angle of release before the projectile is launched, one can influence factors like the maximum height reached, the horizontal distance traveled (range), and the total time the projectile remains in the air.
3. How does the angle of release affect the maximum height achieved by a projectile?
According to the information provided, there is a direct relationship between the angle of release and the maximum height a projectile reaches. A higher projection angle will result in the projectile achieving a greater maximum height. The provided table illustrates this with increasing maximum heights as the angle of release goes from 0 to 90 degrees.
4. What angle of release is generally considered optimal for achieving the greatest horizontal distance (range) when the launch and landing heights are the same (relative projection height is zero)?
When the projectile is launched and lands at the same height, the sources indicate that an angle of release close to 45 degrees will generally result in the greatest maximum horizontal distance. The provided table supports this, showing the maximum distance achieved at a 45-degree angle compared to other angles.
5. Does the angle of release affect the total time of flight of a projectile?
Yes, the angle of release significantly affects the maximum time of flight. As the angle of release increases from 0 to 90 degrees, the provided simulation data shows a corresponding increase in the maximum time of flight. This is because a larger vertical component of the initial velocity (achieved with a higher release angle) keeps the projectile in the air for a longer duration.
6. Are there any tools or simulations available to further explore the relationship between the angle of release and projectile motion?
Yes, the sources mention a "Angle of release projectile motion model for exercise sports science JavaScript HTML5 Applet Simulation Model" available through Open Educational Resources / Open Source Physics @ Singapore. This interactive simulation allows users to explore how different angles of projection affect the trajectory, maximum height, and distance of a projectile. The provided embed code suggests this model can be integrated into web pages for direct use.
7. Is air resistance considered in the projectile motion model discussed in these sources?
For simplicity, the projectile motion model described in these sources considers air resistance to be negligible. This simplification allows for a clearer understanding of the fundamental effects of gravity and the angle of release on the projectile's path. In real-world scenarios, air resistance can play a significant role and alter the actual trajectory.
8. Can the principles of projectile motion, particularly the angle of release, be applied to various sports?
Yes, the principles of projectile motion and the concept of the optimal angle of release are highly relevant to a wide range of sports involving throwing, launching, or projecting objects (or even the human body). Examples mentioned include shot put, javelin, and pole-vaulting. Understanding and optimizing the angle of release is crucial for athletes to maximize performance in these activities, whether it's achieving the greatest distance or height
- Details
- Written by Jonathan
- Parent Category: Interactive Resources
- Category: Physical & Sports Education
- Hits: 11626


 3 2.png
)