About

http://phet.colorado.edu/en/simulation/under-pressure

Briefing Document: Pressure and Related Physics Simulations

Date: October 26, 2023 Subject: Analysis of "Pressure by PhET" and related Open Educational Resources from Open Source Physics @ Singapore. Prepared For: Educational Stakeholders, Curriculum Developers, Physics Educators Prepared By: Bard

1. Introduction

This briefing document analyzes the provided source, focusing on the "Pressure by PhET" simulation and its place within a larger context of open educational resources for physics. The document will highlight the key concepts related to pressure, prior student knowledge, and difficulties, and also give a brief overview of the breadth of other educational resources on this site.

2. Key Concepts of Pressure from "Pressure by PhET" Resource

The "Pressure by PhET" resource focuses on fundamental concepts of pressure, specifically targeted at secondary and junior college students. Key ideas include:

• Definition of Pressure: Pressure is defined as force per unit area (p = F/A). This basic definition is highlighted as a foundational concept.
• Quote: "Pressure = force per unit area (p = F/A)."
• Hydraulic Systems: The resource explains how pressure is transmitted in hydraulic systems. It emphasizes that the incompressibility of liquids is essential for the operation of these systems. When pressure is applied to an enclosed liquid, the pressure is transmitted equally throughout.
• Quote: "The transmission of pressure in hydraulic systems is used in machines e.g. the hydraulic press. Hydraulic systems work due to the incompressibility of liquid and if pressure is applied to one part of an enclosed liquid, the pressure is transmitted to all parts of the liquid."
• Pressure in a Liquid Column: The document covers the relationship between the height of a liquid column, its density, and the gravitational field strength and the pressure exerted by the column. This is expressed by the formula p = hρg. This formula allows one to calculate pressure at a certain depth in a fluid.
• Quote: "Pressure due to a liquid column = height of column x density of the liquid x gravitational field strength (p = hρg)."
• Pressure in Fluids: The source emphasizes that pressure at the same depth in a fluid acts equally in all directions, which helps introduce concepts of isotropy in liquids. It also notes that this concept is often a source of difficulty for students.
• Atmospheric Pressure: The resource also touches upon the idea that atmospheric pressure is the weight of air above the Earth and how our bodies have adapted to balance this pressure, so we don't normally feel it.
• Quote: "The weight of air above the Earth exerts an atmospheric pressure. The pressure inside our bodies balances the atmospheric pressure, so we do not normally feel it"

3. Student's Prior Knowledge and Difficulties

The document acknowledges that students entering this area of study are expected to:

• Understand pressure as force divided by area and apply this understanding to common scenarios such as cutting with a knife or the use of skis on snow.
• _Quote: "Students define: • pressure as force/area, (p = F/A) and use the concept of pressure to explain relevant everyday events (e.g. cutting with a knife, use of skis on snow)."
• Comprehend the moment of force (torque) as force multiplied by the perpendicular distance from the pivot point.
• _Quote: "• the moment of a force or torque (turning effect of a force) about a point as force x perpendicular distance from the pivot (or fulcrum) to the line of action of the force (principle of moments is not required)"

However, the document also notes a key misconception students often have:

• Misconception about Pressure Direction: Students tend to believe that pressure acting downwards in a fluid is greater than pressure acting in other directions at the same depth.
• Quote: "Students have difficulty understanding that pressure at the same depth of a fluid is the same in all directions. They tend to think that the pressure acting downwards is greater."

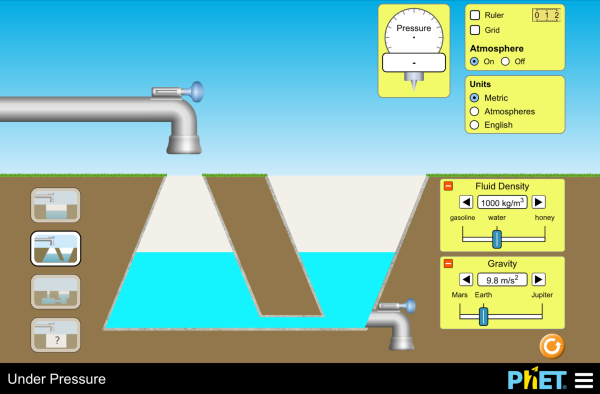
4. The "Pressure by PhET" Interactive Simulation

The resource mentions the use of the "Pressure by PhET" simulation, embedding it directly in the webpage through an iframe. This suggests an emphasis on using interactive simulations for hands-on learning and conceptual understanding. PhET simulations, developed by the University of Colorado Boulder, are known for their interactive, visual, and research-backed approach to learning.

5. Breadth of Open Educational Resources

The provided source includes a large list of other interactive resources. These resources, typically built as Java or JavaScript simulations, cover various topics, including:

• Mechanics: Newtonian mechanics, gravity, projectile motion, circular motion, harmonic motion (spring mass systems and pendulums).
• Electromagnetism: Electric and magnetic fields.
• Waves and Optics: Interference, diffraction, and wave properties.
• Thermodynamics: Ideal Gas Model and Kinetic Theory of Gas
• Modern Physics: Nuclear Decay
• Mathematics: Desmos and GeoGebra modeling tools
• Tools Vernier Caliper

These interactive resources also include Tracker video analysis and modeling software as well as simulations of physical devices. This indicates that the platform is geared toward both theory and practical application. The list also indicates a commitment to using modeling for the study of physics concepts.

The resources also point to a variety of workshops and lectures for educators on using these tools, suggesting a focus on professional development for teachers.

6. Themes and Pedagogical Implications:

• Active Learning: The emphasis on interactive simulations (PhET, EJS) promotes an active learning approach, encouraging students to explore concepts rather than passively receiving information.
• Visual Learning: The use of simulations allows for the visual representation of complex phenomena, which can aid student understanding.
• Addressing Misconceptions: The explicit acknowledgement of common student difficulties highlights the importance of addressing these misconceptions through targeted instruction.
• Real-World Relevance: The reference to applications in hydraulic systems and other everyday examples helps students see the relevance of the concepts.
• Open Resources: The open educational resources allow educators to utilize materials in different contexts.

7. Conclusion

The "Pressure by PhET" resource is a part of a broader ecosystem of interactive physics simulations and educational materials. These resources leverage technology to enhance learning, promote active student engagement, and address common student difficulties in physics. The focus on modeling, simulations, and professional development suggests a commitment to innovative, research-backed pedagogy in physics education.

Pressure Study Guide

Short Answer Quiz

1. Define pressure in terms of force and area.
2. Explain how pressure is transmitted in a hydraulic system.
3. What property of liquids enables hydraulic systems to function?
4. State the formula for calculating pressure due to a liquid column.
5. How does pressure in a liquid act at a given depth?
6. Name two instruments that use a liquid column to measure pressure.
7. What causes atmospheric pressure?
8. Why don't we usually feel atmospheric pressure?
9. Give a brief example of a real world application of pressure.
10. What is one common misconception students have regarding fluid pressure?

Short Answer Quiz Answer Key

1. Pressure is defined as force exerted per unit area. It is calculated by dividing the force applied by the area over which that force is distributed. (p=F/A)
2. Pressure in a hydraulic system is transmitted equally throughout the enclosed liquid. This occurs because the liquid is incompressible, allowing applied pressure at one point to be transferred to all parts of the liquid.
3. The incompressibility of the liquid is what enables hydraulic systems to function. Because liquids cannot be compressed, applied pressure is transmitted rather than absorbed.
4. The pressure due to a liquid column is calculated using the formula: p = hρg, where h is the height of the column, ρ is the density of the liquid, and g is the gravitational field strength.
5. Pressure at any one depth in a liquid acts equally in all directions. This means the pressure is the same whether it is acting up, down, or sideways.
6. A barometer and a manometer use liquid columns to measure atmospheric pressure and pressure differences, respectively.
7. Atmospheric pressure is caused by the weight of the air above the Earth's surface. The air has mass, which exerts a force due to gravity, resulting in pressure.
8. We don't normally feel atmospheric pressure because the pressure inside our bodies balances it out. This internal pressure counteracts the external force and keeps us from feeling the weight of the atmosphere.
9. Cutting with a knife demonstrates how a small area concentrates pressure. The sharp edge of a knife allows a small applied force to exert a high pressure to cut through material, and skis on snow distribute weight over a large surface to lessen pressure and prevent sinking into the snow.
10. Students often incorrectly assume that the pressure acting downwards in a fluid is greater than the pressure acting in other directions at the same depth, failing to understand the isotropic nature of fluid pressure.

Essay Questions

1. Discuss the practical applications of hydraulic systems, explaining how the principles of pressure transmission allow them to operate and provide real-world examples of the use of hydraulic systems in machines and devices.
2. Explain how a barometer and a manometer measure pressure, emphasizing the underlying physical principles related to fluid pressure and the relationship of pressure to the height of a liquid column and give practical examples of how each instrument might be used.
3. Analyze the relationship between pressure, force, and area. Explain how changing each variable individually impacts the others. Provide examples of applications, and practical considerations of these relationships in everyday life.
4. Explain why it is essential to understand the concept of pressure in both fluids and solids and give specific examples of different uses. Consider how an understanding of pressure leads to practical inventions and designs that affect our lives.
5. Contrast the concept of pressure in a liquid at rest with the concept of atmospheric pressure. Explain the difference in their origins, how each is measured, and how they can influence each other and provide everyday examples.

Glossary of Key Terms

Pressure: Force applied perpendicular to the surface of an object per unit area, measured in pascals (Pa) or N/m². (p=F/A)

Hydraulic System: A system that uses incompressible fluids (typically liquids) to transmit pressure from one point to another and perform work.

Incompressibility: A property of a substance (like a liquid) that resists changes in its volume when subjected to pressure, making it an ideal medium for transmitting pressure.

Liquid Column: A column of liquid, the height of which can be used to determine pressure using the formula: p = hρg.

Density (ρ): The mass of a substance per unit volume, often measured in kilograms per cubic meter (kg/m³).

Gravitational Field Strength (g): The acceleration due to gravity, approximately 9.8 m/s² near the Earth’s surface.

Barometer: An instrument that measures atmospheric pressure, often using the height of a mercury column.

Manometer: An instrument that measures pressure differences, often using the height of a liquid column.

Atmospheric Pressure: The pressure exerted by the weight of the air above a particular point, typically decreasing with altitude.

Torque: The tendency of a force to rotate an object around an axis; also known as the moment of a force. (Torque = Force x perpendicular distance).

Key inquiry question: What are the characteristics and effects of forces in nature?

3. Pressure • Pressure = force per unit area (p = F/A).

• The transmission of pressure in hydraulic systems is used in machines e.g. the hydraulic press. Hydraulic systems work due to the incompressibility of liquid and if pressure is applied to one part of an enclosed liquid, the pressure is transmitted to all parts of the liquid.

• Pressure due to a liquid column = height of column x density of the liquid x gravitational field strength (p = hρg).

• Pressure at any one depth in a liquid acts equally in all directions. The height of a liquid column may be used in instruments such as a barometer and manometer to measure the atmospheric pressure and pressure differences.

• The weight of air above the Earth exerts an atmospheric pressure. The pressure inside our bodies balances the atmospheric pressure, so we do not normally feel it 

Students’ prior knowledge of Forces

 Students define:

• pressure as force/area, (p = F/A) and use the concept of pressure to explain relevant everyday events (e.g. cutting with a knife, use of skis on snow).

• the moment of a force or torque (turning effect of a force) about a point as force x perpendicular distance from the pivot (or fulcrum) to the line of action of the force (principle of moments is not required)

Students’ Knowledge and Difficulties in Forces Pressure in a fluid:

Students have difficulty understanding that pressure at the same depth of a fluid is the same in all directions. They tend to think that the pressure acting downwards is greater.

Software Requirements

[SIMU_SWREQ]

Credits

PhET

Frequently Asked Questions about Pressure

1. What is the definition of pressure, and how is it calculated? Pressure is defined as the force acting perpendicularly on a surface per unit area. It's mathematically expressed as Pressure (p) = Force (F) / Area (A). This means that for the same force, a smaller area will result in a higher pressure.
2. How does pressure work in hydraulic systems, and what principle is involved? Hydraulic systems use the principle that pressure applied to an enclosed liquid is transmitted undiminished to all parts of the liquid. Because liquids are nearly incompressible, when a force is applied to a small area of a liquid (e.g. piston), the pressure change is transmitted to a larger area, creating a larger output force. This is the basis for machines like the hydraulic press.
3. How is the pressure of a liquid column calculated, and what factors affect it? The pressure due to a liquid column is calculated using the formula p = hρg, where 'h' represents the height of the liquid column, 'ρ' (rho) is the density of the liquid, and 'g' is the gravitational field strength (approximately 9.8 m/s² on Earth). This shows that pressure increases with depth, density, and gravitational strength.
4. Does pressure in a liquid act differently depending on direction? No, pressure at any given depth in a liquid acts equally in all directions. A common misconception is that pressure acts more strongly downwards; however, at the same depth, the pressure is the same in all directions.
5. What is atmospheric pressure, and why don't we feel it all the time? Atmospheric pressure is the weight of the air above us exerting force on the surface of the Earth. While it is substantial, we don't feel it because the pressure inside our bodies balances the external atmospheric pressure.
6. How are barometers and manometers used in the context of pressure? Barometers and manometers utilize the height of a liquid column to measure pressure. A barometer typically measures atmospheric pressure, while a manometer measures pressure differences, such as that between the gas in a container and the atmospheric pressure.
7. What prior knowledge should students have before studying pressure? Students should understand the basic definition of force, and also understand force per unit area. They should be able to relate the idea of pressure to everyday situations (like cutting with a knife or using skis on snow) where forces act on specific areas. Additionally, they should have some understanding of torque, although a formal understanding of the principle of moments is not required.
8. What are some common misconceptions that students have about pressure in fluids? A common difficulty for students is understanding that pressure at the same depth of a fluid is the same in all directions. Students tend to think the pressure acting downwards is greater.