About

1.2.5 Example

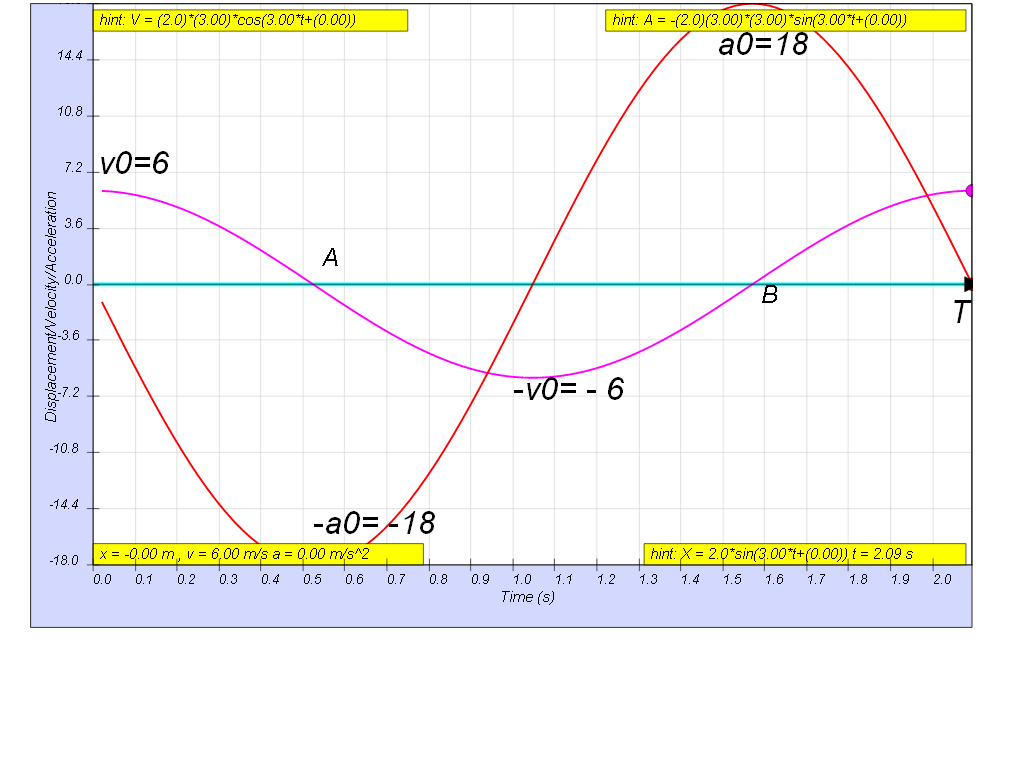
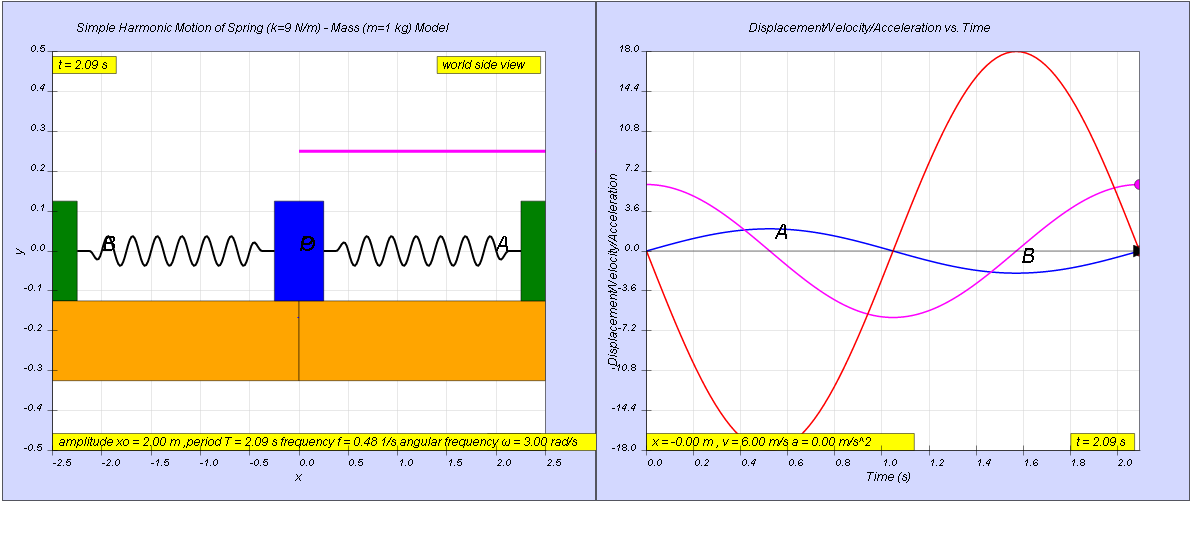
The graphs show how the variation with time of the velocity, v and the acceleration, a of a body when it is oscillating with simple harmonic motion.
(a)    Determine the period, T.
(b)    Sketch the variation with time of the displacement, x, of the oscillating body
[ 2.09 s, x = 2  sin( 3t )]

1.2.5.1 Solution:

a) maximum velocity , v₀ = x₀ω = 6 m/s

maximum acceleration a₀ = x₀ω² = 18 m/s²

thus dividing the 2 equations, we get ω = 3 rad/s

therefore since $\omega =\genfrac{}{}{0.1ex}{}{2\pi }{T}$

using the model to test check out your answer!

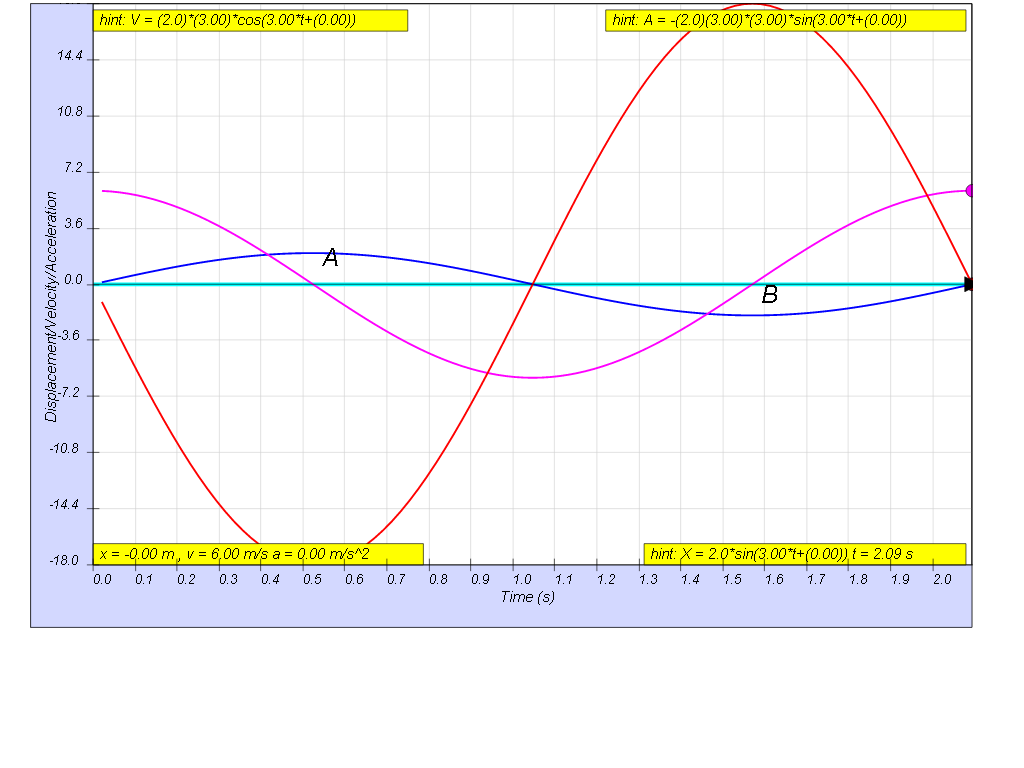
1.2.5.2 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/73

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM11/SHM11_Simulation.xhtml