About

1.2.4 Acceleration

 

From v = v_o cos ω t = x₀ ω cos ω t

where x_o is the maximum displacement

differentiating we get

 $$a=\frac{dv}{dt}=-<!--\; -\; -->{\omega }^2(x_{0}sin\omega t)=-<!--\; -\; -->{\omega }^{2}x$$
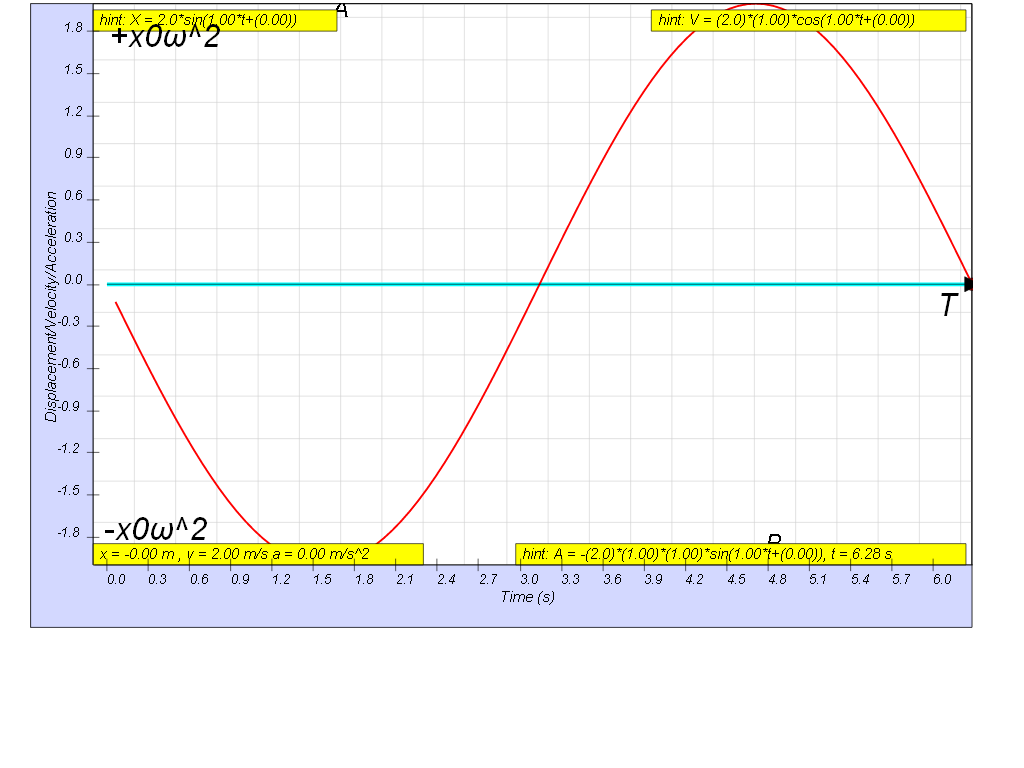
  Variation with time of acceleration   

In terms of x:

 
Therefore,  a = - xo ω² sin ω t
                   = - ω² (x_o sin ω t)
which is the defining equation for S.H.M. !
               a     = - ω² x
 
 
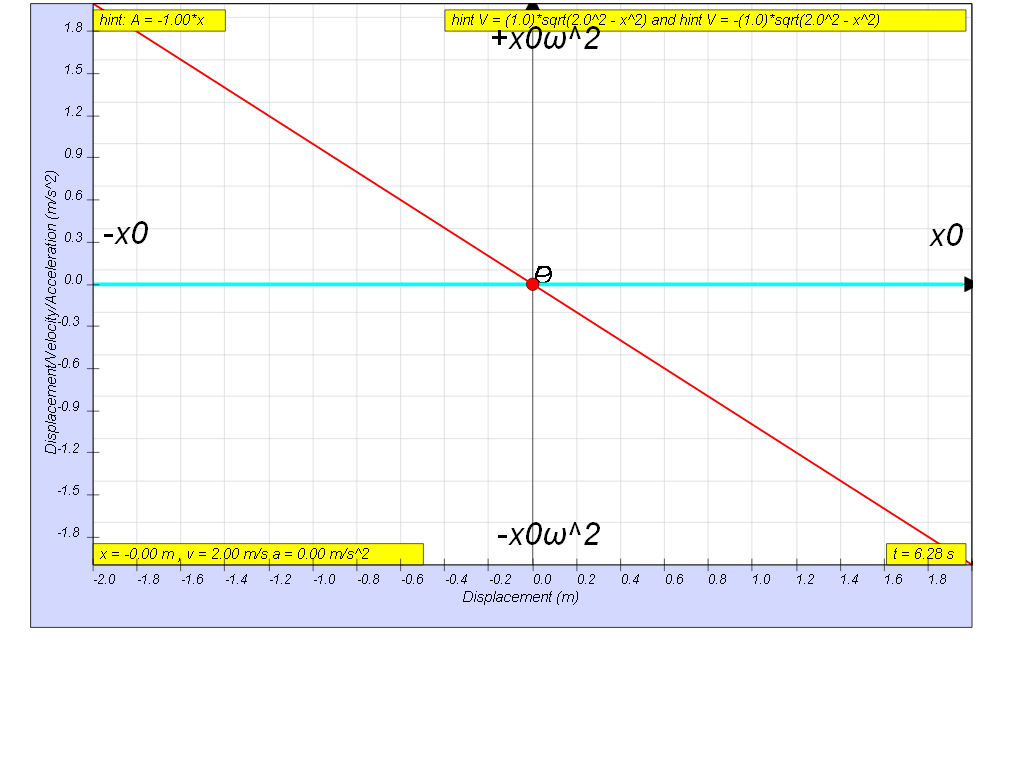
Variation with displacement of acceleration 

since 
   
        a = – a₀sin ω t         

where a_o is the maximum acceleration
where by a₀ = ω² (x_o)  

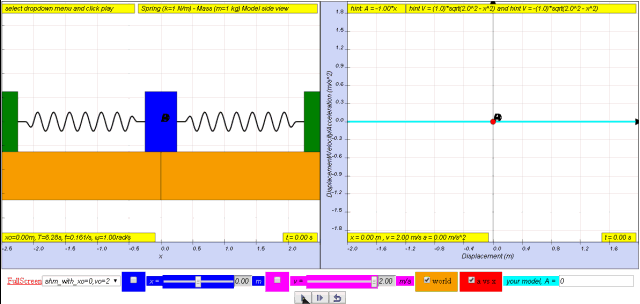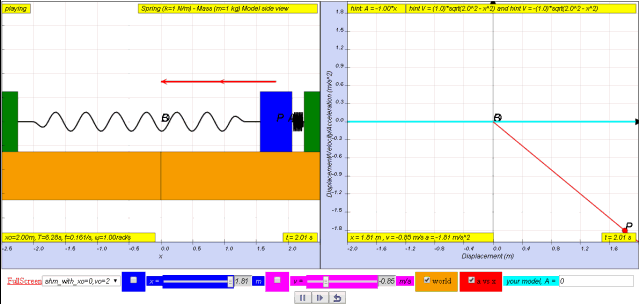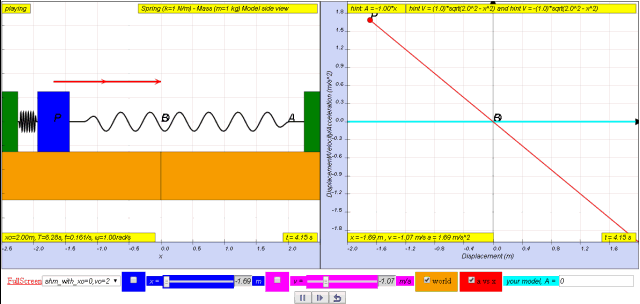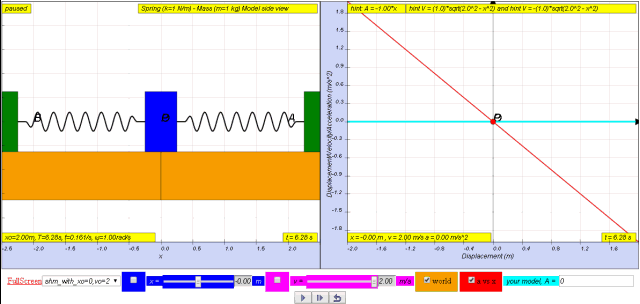
1.2.3.1 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/74

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM10/SHM10_Simulation.xhtml