About

1.2.6 Example 

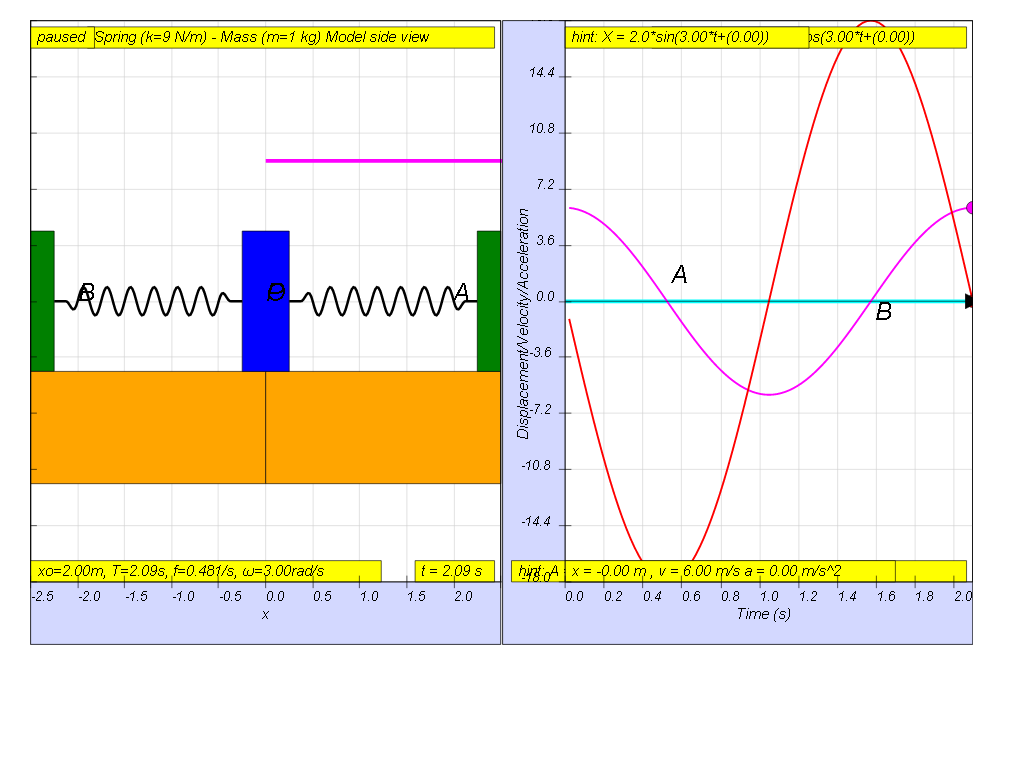
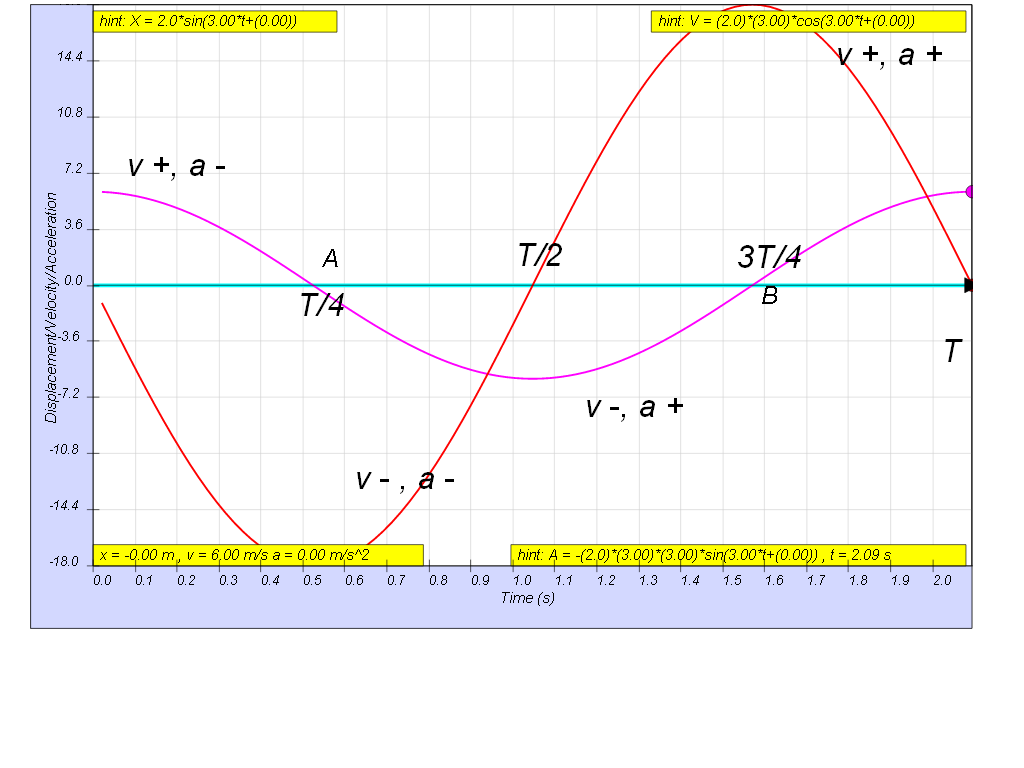
The diagram shows the displacement-time graph for a body performing simple harmonic motion. Suggest in terms of period T the following
(a)    range of time where the velocity and acceleration are in same direction.
(b)    range of time where the velocity and acceleration are in opposite directions

suggested answers

$\genfrac{}{}{0.1ex}{}{T}{4}<t<\genfrac{}{}{0.1ex}{}{T}{2}and\genfrac{}{}{0.1ex}{}{3T}{4}<t<T$

$0<t<\genfrac{}{}{0.1ex}{}{T}{4}and\genfrac{}{}{0.1ex}{}{T}{2}<t<\genfrac{}{}{0.1ex}{}{3T}{4}$

1.2.6.1 Solution:

1.2.6.2 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/75

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM12/SHM12_Simulation.xhtml