About

Subject Area	Waves & Optics
Levels	First Year and Beyond the First Year
Available Implementation	Python & Easy JavaScript Simulation
Learning Objectives	Students who complete this set of exercises will be able to obtain and use information from peer-reviewed literature. Plot an equation over a range of values. Analyze and compare plots (Exercises 1 and 2); write the deflection angle in terms of the relative index of refraction to calculate the deflection angle of rays entering spherical drops (Exercises 3 and 4); produce and describe graphs of deflection angle versus incident angle for light of different wavelengths (Exercises 3 and 4). identify rainbow angles for light of different wavelengths (Exercises 3 and 4); and crudely estimate the intensity as a function of detection angle (Exercise 5).
Time to Complete	120 min

This set of exercises may be used in an introductory course that covers optics or in an upper-level optics course. The first three computational exercises are not demanding, but collectively provide an opportunity to deduce physical consequences (e.g., why is it that the primary and secondary rainbows are bright in particular directions). The last exercise is intended purely as a crude, ‘zeroeth order’ estimate of the irradiance as a function of deflection angle, purposefully neglecting polarization effects. Additional computational exercises have been described by D.S. Amundsen et al., Am. J. Phys. 77 (9), 795-798 (2009). An experimental apparatus to explore rainbows up to the 6th order has been described by G. Casini and A. Covello, Am. J. Phys. 80 (11), 1027-1034 (2012).

For Exercises 3 and 4, the theoretical concepts required are the Law of Refraction and the Law of Reflection, which are standard topics in introductory courses and are usually revisited in intermediate or advanced optics courses.

For Exercise 5, the crude model is nothing more than summing the irradiances associated with different rays, which implicitly assumes that the rays are incoherent with one another. Depending on the course, this can be contrasted with the ideas underlying the derivation of far field diffraction patterns - namely, that one works with the electric fields and carefully accounts for the relative phases of contributions from different parts of an extended source.

EXERCISE 2: DEFLECTION ANGLE FOR A LIGHT RAY ENTERING A SPHERICAL RAINDROP

Assume that a light ray incident on a spherical raindrop at an angle θ1i measured with respect to the surface normal undergoes one internal reflection before leaving the raindrop, as shown below.

`

Show that if θi≡θ1i and θr≡θ1t, then the deflection angle δ of the light ray is (in radians):

The deflection angle δ is the angle between the incident ray and the outgoing ray, and θr is the angle of refraction for the light ray incident from air and entering water. To compute the deflection angle, what quantities must be known?

EXERCISE 3: COMPUTE THE DEFLECTION ANGLE VERSUS INCIDENT ANGLE

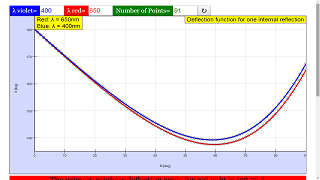
Generate a plot of the deflection angle δ as a function of incident angle θi for light rays of wavelength 400 nm that experience one internal reflection in the raindrop. Compare, on the same plot, the deflection angle for light rays of wavelength 650 nm. The two curves should have minima that are close to each other, but not identical. What are the values of the incident angle corresponding to these two minima? Assuming that these minima correspond to the rainbow direction, what direction do you have to look relative to the horizontal to see the bright red band of the rainbow? What direction do you have to look relative to the horizontal to see the bright violet band? Which band appears higher in the sky?

Near the minimum of the deflection function (that is, the δ(θi) curve), are two rays with slightly different incident angles deflected into different directions? Regarding the brightness of the deflected light perceived by an observer, what is implied by your answer?

EXERCISE 1: OBTAIN AND USE INFORMATION FROM PEER-REVIEWED LITERATURE

Water and air are the two materials involved with producing rainbows we may see in the sky after a thunderstorm. To accurately predict where rainbows will appear, we need to have accurate information about the refractive indices of water and air.

(a) Obtain a copy of “Models for the wavelength dependence of the index of refraction of water”, Applied Optics 36 (16), 3785-3787 (1997) by Paul D.T. Huibers, and use Eq. (3) of that paper to generate a plot of the refractive index of water as a function of wavelength in the range from 400 to 650 nm.

(b) Obtain a copy of “Refractive index of air: new equations for the visible and near infrared”, Applied Optics 35(9), 1566-1573 (1996) by Philip E. Ciddor, and use Eq. (1) of that paper to generate a plot of nair−1$n_{air}-1$, the deviation of the refractive index of air from unity, as a function of wavelength in the range from 400 to 650 nm.

Which material has the larger change in refractive index over the wavelength range from 400 to 650 nm? Calculate the ratio of the larger change to the refractive index of the material for a wavelength of 400 nm, and comment on the magnitude of the ratio.

EXERCISE 2: DEFLECTION ANGLE FOR A LIGHT RAY ENTERING A SPHERICAL RAINDROP

Assume that a light ray incident on a spherical raindrop at an angle θ1i${\theta }_{1i}$ measured with respect to the surface normal undergoes one internal reflection before leaving the raindrop, as shown below.

`

Show that if θi≡θ1i${\theta }_i\equiv {\theta }_{1i}$ and θr≡θ1t${\theta }_r\equiv {\theta }_{1t}$, then the deflection angle δ$\delta$ of the light ray is (in radians):

The deflection angle δ$\delta$ is the angle between the incident ray and the outgoing ray, and θr${\theta }_r$ is the angle of refraction for the light ray incident from air and entering water. To compute the deflection angle, what quantities must be known?

EXERCISE 3: COMPUTE THE DEFLECTION ANGLE VERSUS INCIDENT ANGLE

Generate a plot of the deflection angle δ$\delta$ as a function of incident angle θi${\theta }_i$ for light rays of wavelength 400 nm that experience one internal reflection in the raindrop. Compare, on the same plot, the deflection angle for light rays of wavelength 650 nm. The two curves should have minima that are close to each other, but not identical. What are the values of the incident angle corresponding to these two minima? Assuming that these minima correspond to the rainbow direction, what direction do you have to look relative to the horizontal to see the bright red band of the rainbow? What direction do you have to look relative to the horizontal to see the bright violet band? Which band appears higher in the sky?

Near the minimum of the deflection function (that is, the δ(θi)$\delta ({\theta }_i)$ curve), are two rays with slightly different incident angles deflected into different directions? Regarding the brightness of the deflected light perceived by an observer, what is implied by your answer?

EXERCISE 4: WHERE IS THE SECONDARY (DOUBLE) RAINBOW?

Repeat the computation of Exercise 3, but now assume that the ray undergoes two internal reflections within the raindrop. In this case, show that the deflection angle is given by

and plot the deflection angle versus the incident angle for rays of wavelength 400 nm and 650 nm. The two curves should have minima that are close to each other, but not identical. What are the values of the incident angle corresponding to these two minima? Assuming that these minima correspond to the rainbow direction, what direction do you have to look relative to the horizontal to see the bright red band of the secondary rainbow? Can a ground based observer see these rays? Do the rays that produce the secondary rainbow enter the top of the raindrop? What direction do you have to look relative to the horizontal to see the bright violet band? Which band appears higher in the sky?

Near the minimum of the deflection function (that is, the δ(θi)$\delta ({\theta }_i)$ curve), are two rays with slightly different incident angles deflected into different directions? Regarding the brightness of the deflected light perceived by an observed, what is implied by your answer?

EXERCISE 5: CRUDE ESTIMATE OF THE IRRADIANCE VERSUS DEFLECTION ANGLE FOR A SINGLE WAVELENGTH: PRIMARY RAINBOW

Assume that the each outgoing ray produces an irradiance that is equal to I(θ)=I0exp[−(θ−δ)2]$I(\theta )=I_0\exp [-(\theta -\delta {)}^2]$ where here the angles are assumed to be in degrees and the implied width of this distribution is 1∘$1^{\circ }$. (For simplicity, we neglect the loss of intensity during refraction and internal reflection. This is a huge oversimplification, but it allows us to focus on adding up contributions from each ray.) Sum up the contributions from rays uniformly distributed over the scaled impact parameter b~=b/R$\tilde{b}=b/R$ to compute the overall irradiance as a function of deflection angle for light of wavelength 400 nm. Plot the resulting irradiance distribution versus deflection angle for a single wavelength. How does this plot help explain why the rainbow is bright?

#

# Primary_Rainbow_Deflection_Function.py

#

# Plot the deflection function

# for the primary (first-order) rainbow

# assuming a spherical water drop

# and a single wavelength,

# which implies a single index of refraction

#

# The refractive index of water is taken from

# Eq. 3 of P.D.T Huibers, Applied Optics,

# Vol. 36, No. 16, pp. 3785-3787 (1997).

#

# The refractive index of air is taken from

# Eq. 1 of P.E. Ciddor, Applied Optics,

# Vol. 35, No. 9, pp. 1566-1573 (1996).

#

# Written by:

#

# Ernest R. Behringer

# Department of Physics and Astronomy

# Eastern Michigan University

# Ypsilanti, MI 48197

# (734) 487-8799

# This email address is being protected from spambots. You need JavaScript enabled to view it.

#

# 20160109 by ERB

#

from __future__ import print_function

from pylab import figure,plot,xlim,xlabel,ylim,ylabel,grid,legend,title,show

from math import pi,asin

from numpy import linspace,sin,zeros,argmin

# Define the index of refraction function for water

def water_index(wavelength):

n_H2O = 1.31279 + 15.762/wavelength - 4382.0/(wavelength**2) + 1.1455e6/(wavelength**3)

return(n_H2O)

# Define the index of refraction function for air

# Note: wavelength is supposed to be in micrometers

def air_index_minus_one(wavelength):

term1 = 0.05792105/(238.0185 - 1.0e6/(wavelength**2))

term2 = 0.00167917/(57.362 - 1.0e6/(wavelength**2))

return(term1+term2)

# Inputs

wavelength_r = 650 # vacuum wavelength in nm ("red")

wavelength_v = 400 # vacuum wavelength in nm ("violet")

n_r = water_index(wavelength_r) # refractive index of water at wavelength_r

n_v = water_index(wavelength_v) # refractive index of water at wavelength_v

npts = 901

n_ar = 1.0 + air_index_minus_one(wavelength_r) # refractive index of air at wavelength_r

n_av = 1.0 + air_index_minus_one(wavelength_v) # refractive index of air at wavelength_v

theta_i_deg = linspace(0.0,90.0,npts) # array of incident angle values [deg]

theta_i = theta_i_deg*pi/180.0 # array of incident angle values [rad]

# Set up the arrays of deflection angles

theta_r = zeros(npts)

theta_v = zeros(npts)

# Calculate the refraction angle for each incident angle

# and for red and for violet light

for j in range(0,npts):

theta_r[j] = asin((n_ar/n_r)*sin(theta_i[j]))

theta_v[j] = asin((n_av/n_v)*sin(theta_i[j]))

# Calculate the deflection angle for each incident angle for red light

theta1r = 2.0*(theta_i - theta_r) + 1.0*(pi - 2.0*theta_r) # First deflection function

theta1r_deg = theta1r*180.0/pi

# Calculate the deflection angle for each incident angle for violet light

theta1v = 2.0*(theta_i - theta_v) + 1.0*(pi - 2.0*theta_v) # First deflection function

theta1v_deg = theta1v*180.0/pi

print("The primary rainbow deflection angle for red light is ",min(theta1r_deg))

# The index of this value is

index_r = argmin(theta1r_deg)

print("This primary rainbow deflection angle for red light corresponds to")

print("an incident angle of ",theta_i_deg[index_r]," deg.")

print("The red band of the primary band appears at ",180.0-min(theta1r_deg)," above the horizontal.")

print(" ")

print("The primary rainbow deflection angle for violet light is ",min(theta1v_deg))

# The index of this value is

index_v = argmin(theta1v_deg)

print("This primary rainbow deflection angle for violet light corresponds to")

print("an incident angle of ",theta_i_deg[index_v]," deg.")

print("The violet band of the primary band appears at ",180.0-min(theta1v_deg)," above the horizontal.")

#----------------------------------------------------------------------

# Start a new figure. This will be a plot of the deflection functions,

# i.e., deflection angle versus incident angle

figure()

# Set the limits of the horizontal axis

xlim(0,90)

# Label the horizontal axis

xlabel("\(\\theta_i\) [deg]", size = 16)

# Set the limits of the vertical axis

ylim(135,185)

# Label the vertical axis

ylabel("\(\\delta\) [deg]", size = 16)

# Draw a grid

grid(True)

# Plot the deflection functions

plot(theta_i_deg,theta1r_deg,"r-",label="\(\lambda = 650 \\, {\\rm nm}\)")

plot(theta_i_deg,theta1v_deg,"b-",label="\(\lambda = 400 \\, {\\rm nm}\)")

# Generate the legend

legend(loc=1)

# Generate the title

title("Deflection function for one internal reflection")

show()

Exercise 1: Obtain and use information from peer-reviewed literature

The plot for the refractive index of water should look like:

`

The plot for the deviation of the refractive index of air from unity should look like:

Exercise 2: Deflection angle for a light ray entering a spherical raindrop

To calculate the deflection angle, one needs to know the refractive index of the air and the water at the particular wavelength and also the angle of incidence of the incoming ray. The laws of refraction and reflection are then applied to obtain the angles of refraction and the angle of reflection for the internal reflection. Students should be able to show that the equalities shown in the figure illustrating the ray/raindrop geometry.

Exercise 3: Compute the deflection angle versus incident angle

The solution for Exercise 3 is:

The minimum of the deflection function for λ=400$\lambda =400$ nm (λ=650$\lambda =650$ nm) is δ=139.3∘$\delta ={139.3}^{\circ }$ (δ=137.6∘)$(\delta ={137.6}^{\circ })$. This means that you must look (with the sun at your back and the distant raindrops in front of you) at an angle of 180∘−139.3∘=40.7∘${180}^{\circ }-{139.3}^{\circ }={40.7}^{\circ }$ (180∘−137.6∘=42.4∘)$({180}^{\circ }-{137.6}^{\circ }={42.4}^{\circ })$ relative to the horizontal to see the bright violet (red) band of the rainbow. So the red band appears above the violet band. (It really does!) It is worth noting that the rays producing the primary rainbow enter the top half of the raindrops.

Exercise 4: Where is the double (secondary) rainbow?

The solution for Exercise 4 is:

The minimum of the deflection function for λ=400$\lambda =400$ nm (λ=650$\lambda =650$ nm) is δ=233.3∘$\delta ={233.3}^{\circ }$ (δ=230.2∘$\delta ={230.2}^{\circ }$). These rays are directed back up into the sky and the ground-based observer won’t see them. However, if you realize that you have just computed the deflection angles for rays entering the bottom half of the raindrop, you realize that you must look (with the sun at your back and the distant raindrops in front of you) at an angle of 233.3∘−180∘=53.3∘,,(230.2∘−180∘=50.2∘)${233.3}^{\circ }-{180}^{\circ }={53.3}^{\circ },,({230.2}^{\circ }-{180}^{\circ }={50.2}^{\circ })$ relative to the horizontal to see the bright violet (red) band of the rainbow. So the red band of the secondary rainbow appears below the violet band. (It really does!). Thus the rays producing the secondary rainbow enter the bottom half of the raindrops and the order of the color bands is reversed relative to the primary rainbow. Comparing these angles to those from Exercise 3, we see that the secondary rainbow appears above the primary rainbow. The reduced brightness of the secondary rainbow is due to the additional internal reflection and the corresponding loss of irradiance during that reflection. It is posible to extend Exercises 3 and 4 to account for the change in intensity occurring for every refraction or internal reflection. For fun, it must be noted that fascination with the double rainbow became an Internet meme in 2010 when a person living on the border of Yosemite National Park recorded his reaction to a spectacular double rainbow. At the time of writing, the video can be seen at: https://www.youtube.com/watch?v=OQSNhk5ICTI).

Exercise 5: Crude estimate of the irradiance versus deflection angle for a single wavelength: Primary Rainbow

The solution for Exercise 5 is:

Note that irradiance is distributed over a large range of detection angles, and that the irradiance has a peak near (but not at) the minimum of the deflection function for these chosen parameters. If we use an angular width smaller than 1∘$1^{\circ }$ for the assumed irradiance distribution of a ray, the irradiance peak approaches the minimum in the deflection angle and the “background irradiance” decreases. The main result is that irradiance accumulates in the direction specified by the minimum in the deflection function because several rays are deflected into essentially the same direction. This is known as rainbow scattering, and it is also observed in scattering events such as atomic/molecular collisions or ion collisions with ordered surfaces.

Most introductory textbooks mention rainbows and the angles at which they can be observed, but do not necessarily explain why rainbows are bright. This set of exercises is intended to show how irradiance “piles up” around the minima of the deflection functions calculated in Exercises 3 and 4.

 

Translations

Code	Language		Translator	Run

Credits

Fremont Teng; Loo Kang Wee

Sample Learning Goals

[text]

For Teachers

Primary Rainbow Deflection Function JavaScript Simulation Applet HTML5

Instructions

Control Panel

Toggling Full Screen

Reset Button

Research

[text]

Video

[text]

 Version:

1. https://www.compadre.org/PICUP/exercises/exercise.cfm?I=129&A=rainbows
2. http://weelookang.blogspot.com/2018/06/primary-rainbow-deflection-function.html 

Other Resources

[text]

end faq

{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}