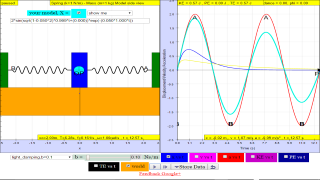
About

1.6 Degrees of damping                    LO (i)

If no frictional forces act on an oscillator (e.g.  mass-spring system, simple pendulum system,  etc.), then it will oscillate indefinitely.

In practice, the amplitude of the oscillations decreases to zero as a result of friction. This type of motion is called damped harmonic motion. Often the friction arises from air resistance (external damping) or internal forces (internal damping).

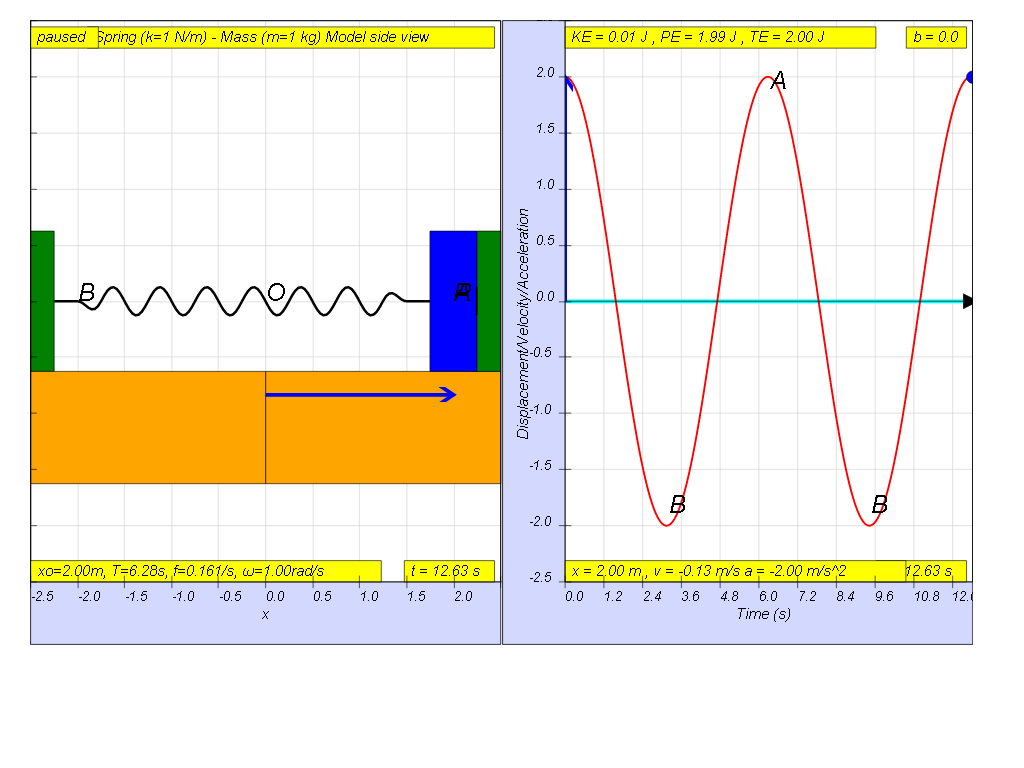
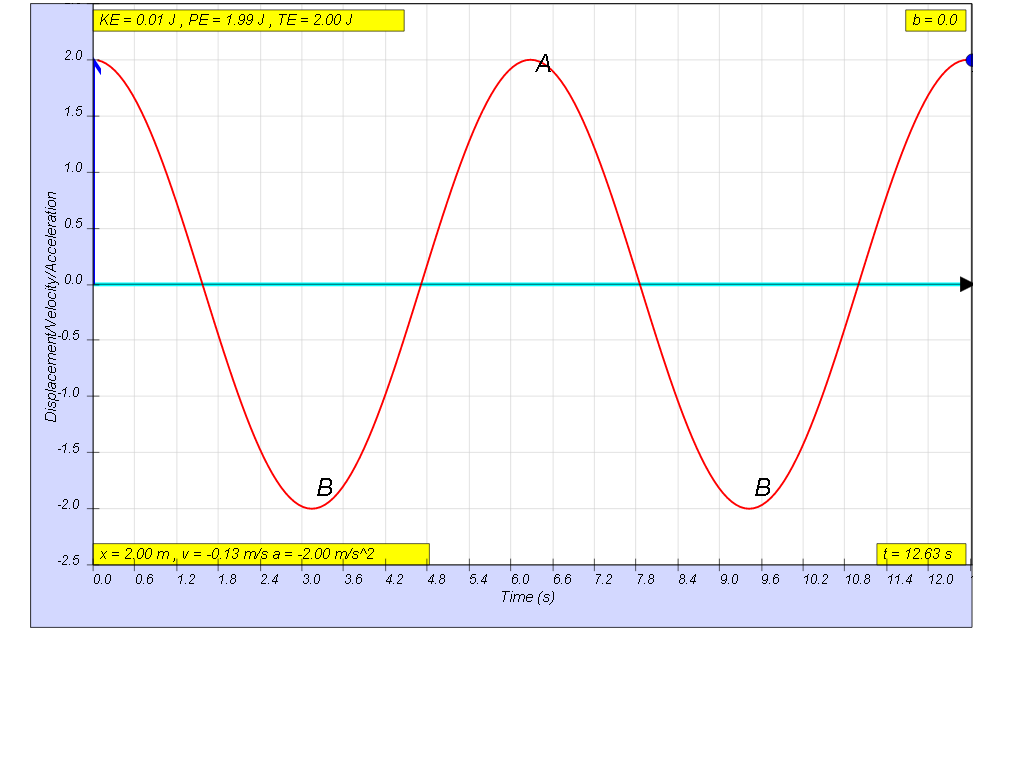
1.6.1 if the motion is x= x₀ sin(ωt), the following are the x vs t graphs for 2 periods, as an illustration of the damping.

1.6.1.1 No damping

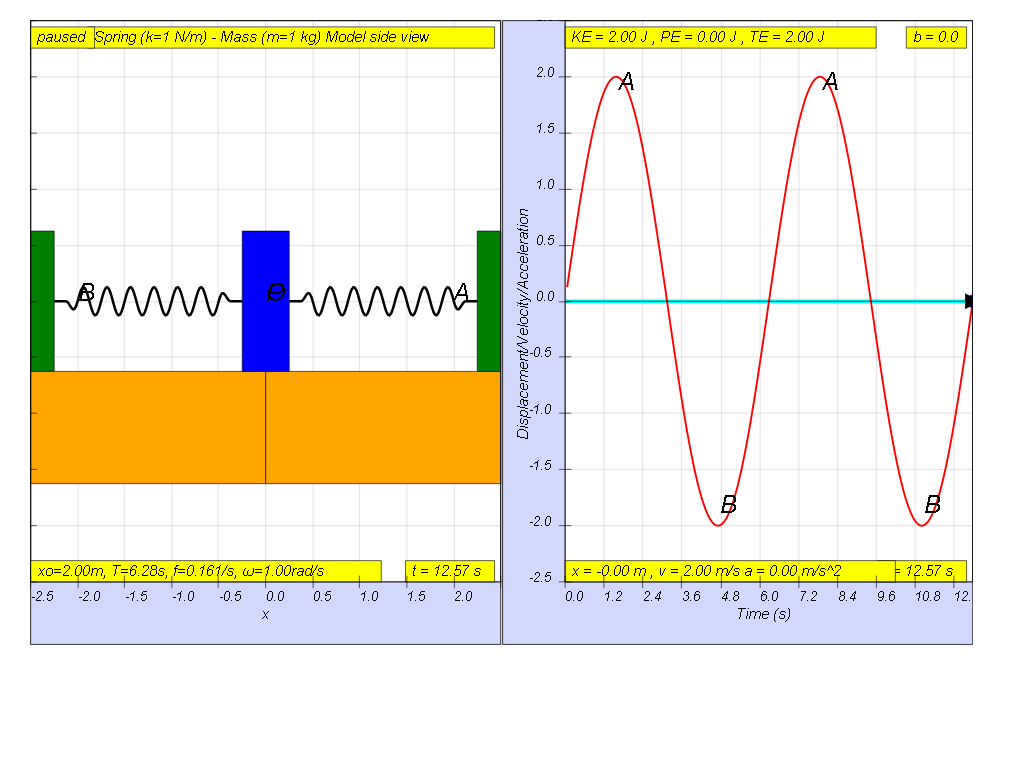
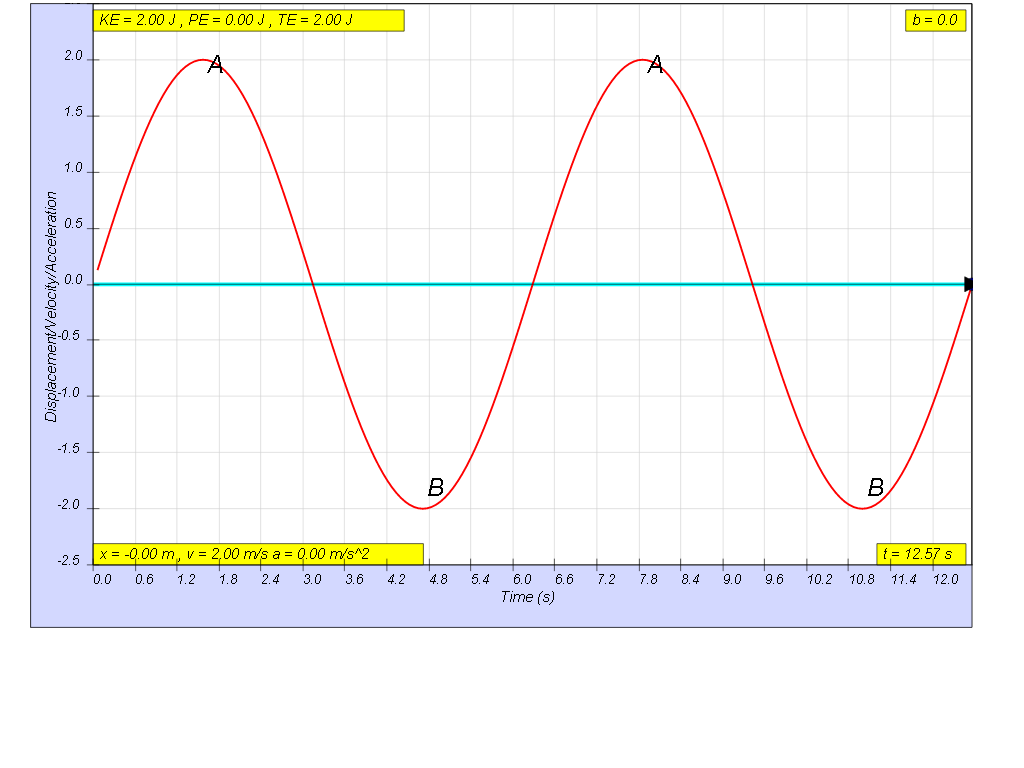
when b=0.0 no damping, system oscillates forever without coming to rest. Amplitude and thus total energy is constant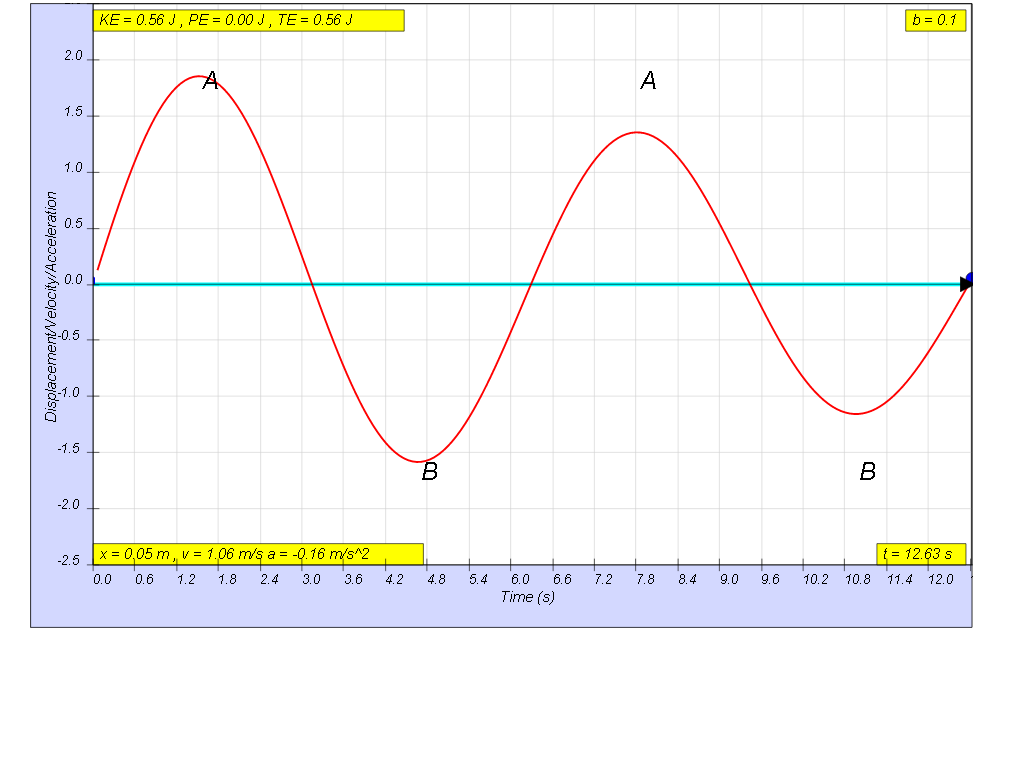

1.6.1.2 Light damping

when b=0.1 very lightly damp, system undergoes several oscillations of decreasing amplitude before coming to rest. Amplitude of oscillation decays exponentially with time.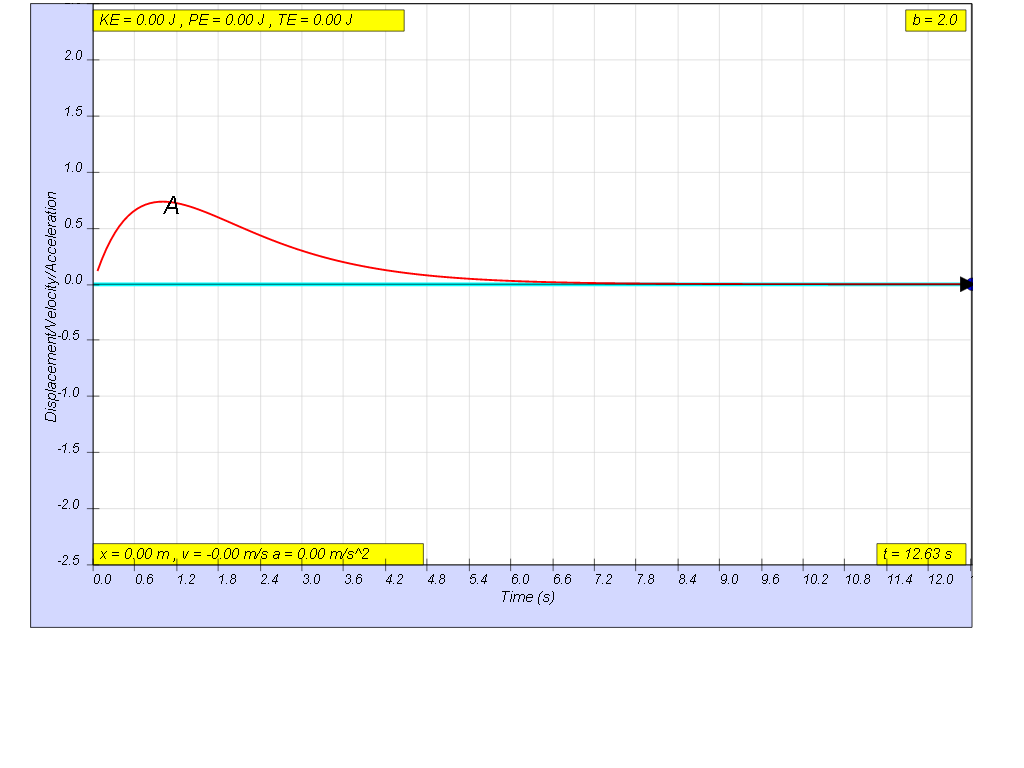

1.6.1.3 Critical damping

when b=2.0, critically damp system returns to equilibrium in the minimum time, without overshooting or oscillating about the equilibrium position amplitude.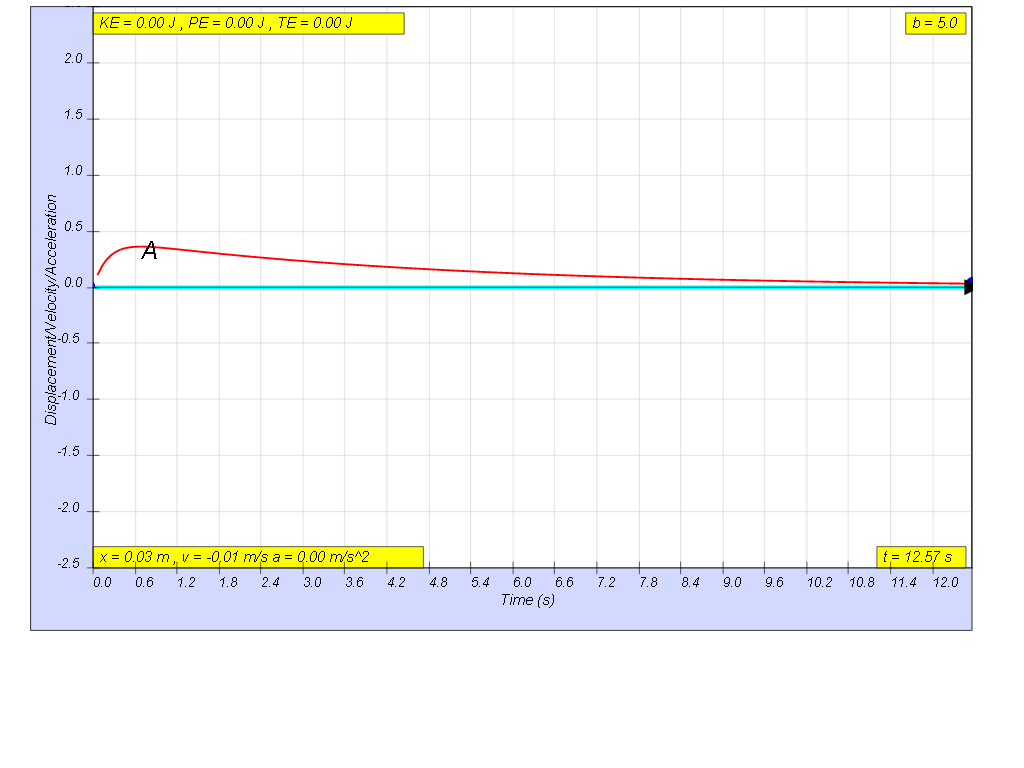

1.6.1.4 Heavy damping

when b=5.0, very heavy damp, system returns to equilibrium very slowly without any oscillation

1.6.2 a more typical starting position, is  x= x₀ cos(ωt), the following are the x vs t graphs for 2 periods, as an illustration of the damping.

1.6.2.1 No damping

when b=0.0 no damping, system oscillates forever without coming to rest. Amplitude and thus total energy is constant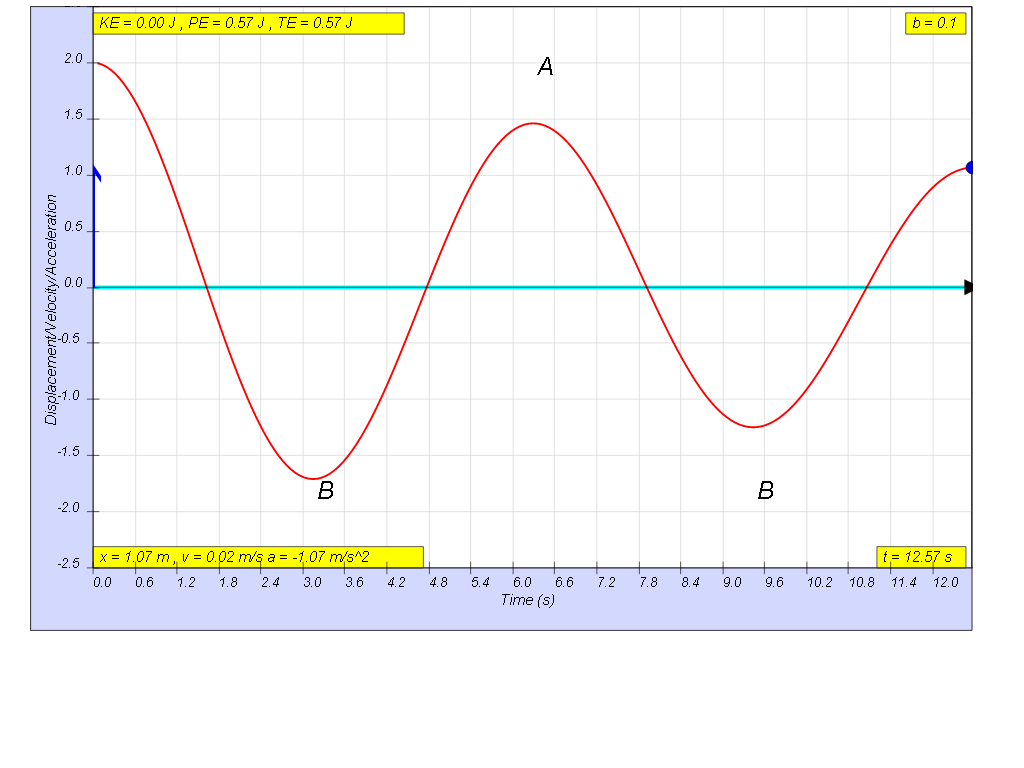

1.6.2.2 Light damping

when b=0.1 very light damping, system undergoes several oscillations of decreasing amplitude before coming to rest. Amplitude of oscillation decays exponentially with time.

1.6.2.3 Critical damping

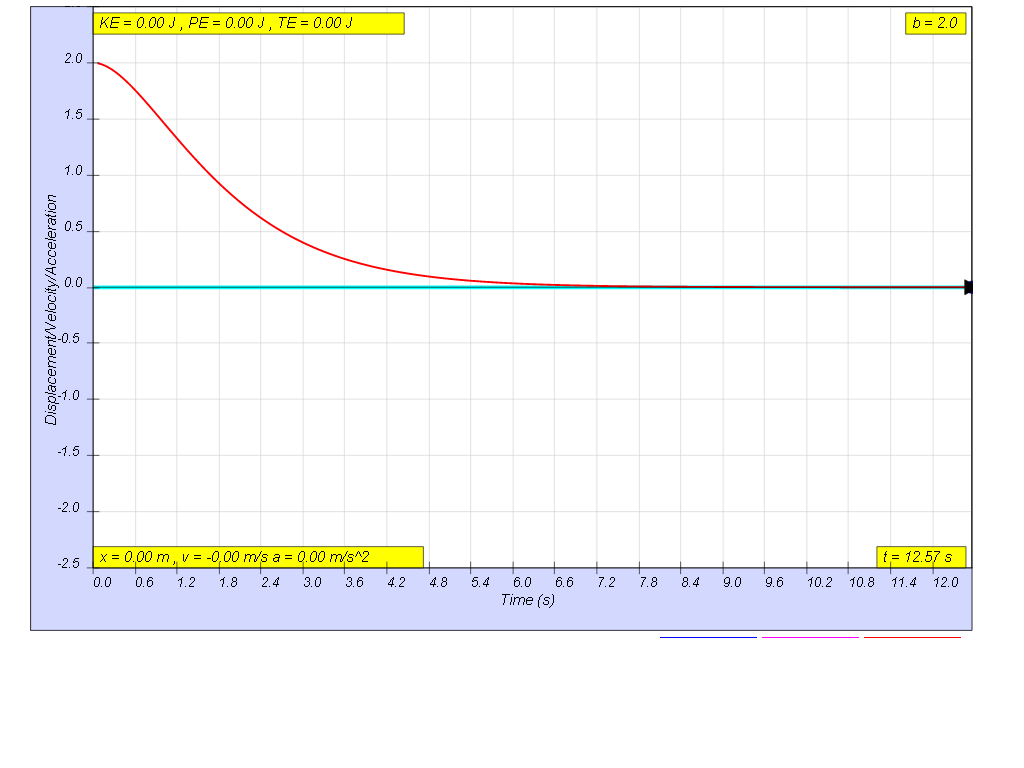
when b=2.0 critically damp, system returns to equilibrium in the minimum time, without overshooting or oscillating about the equilibrium position amplitude.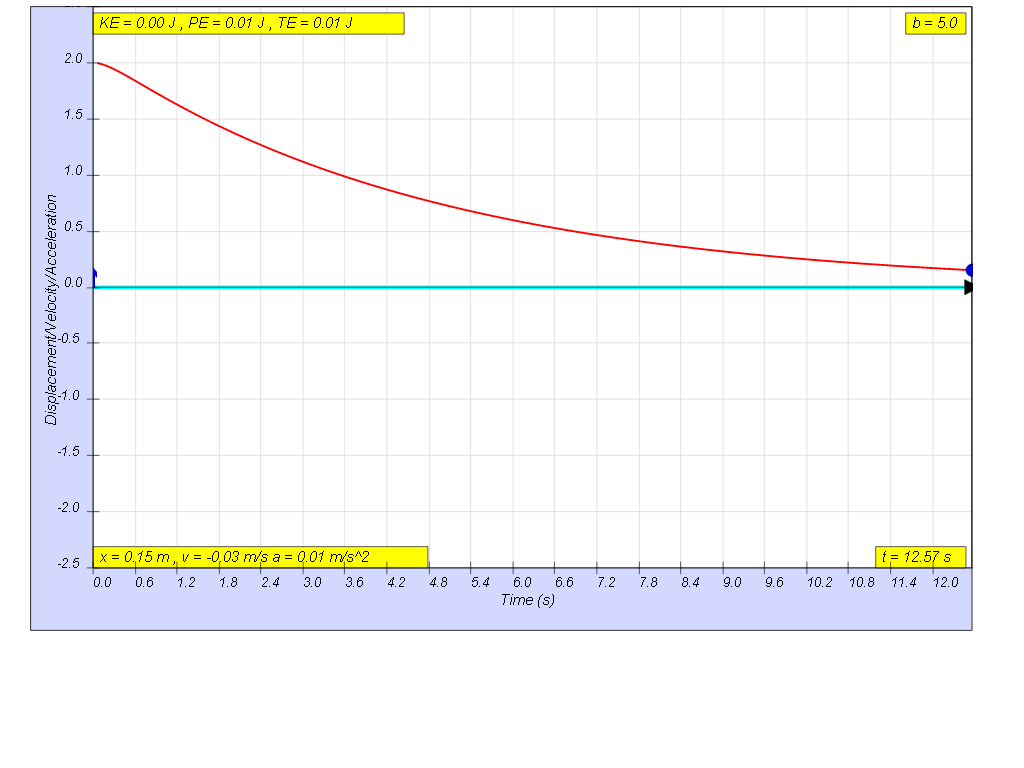

1.6.2.4 Heavy damping

when b=5.0 very heavy damp,  system returns to equilibrium very slowly without any oscillation.

1.6.3 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/84

 

Translations

Code	Language		Translator	Run

Credits

lookang

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM20/SHM20_Simulation.xhtml

Apps

https://play.google.com/store/apps/details?id=com.ionicframework.shm20app163344&hl=en

end faq

{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}