About

1.7.4 The response of the oscillatory system depends on the value of the frequency of the periodic force (also known as the driving frequency).                LO (k)

When the driving frequency f  is close to or equal to the natural frequency f_o of the oscillating system, maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude.  This phenomenon is called resonance.      

 A more accurate and complicated picture could be found on Wikipedia.

 

This computer model can be used to generate a similar data representation when using the instruction found on the html below the model.

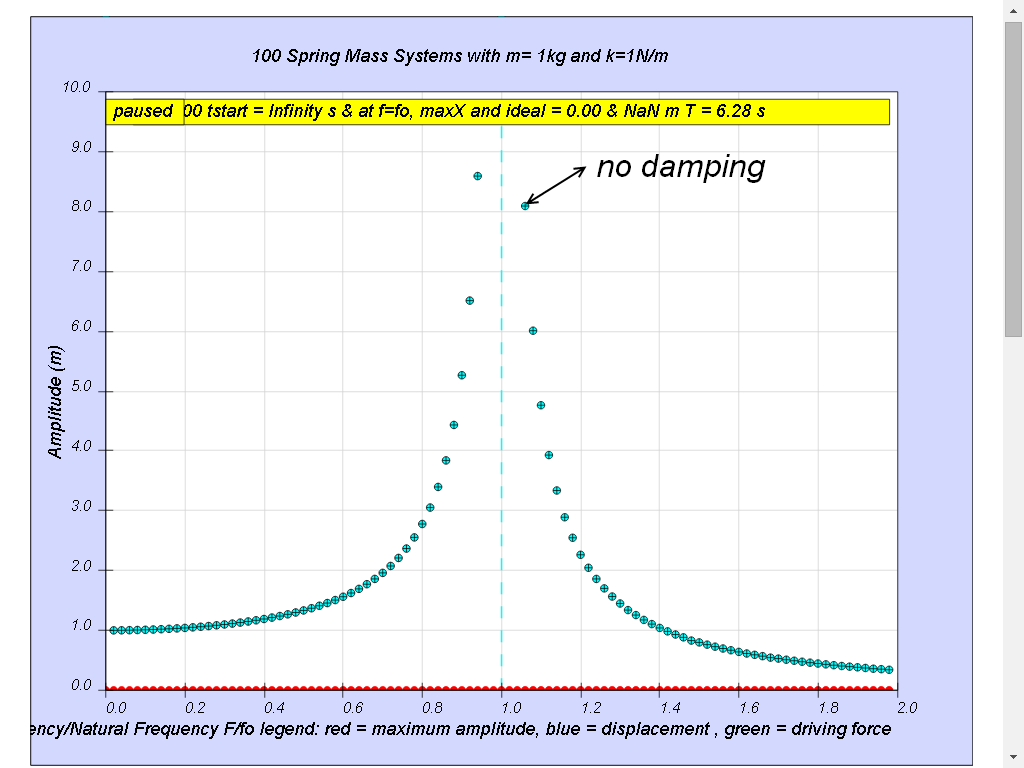
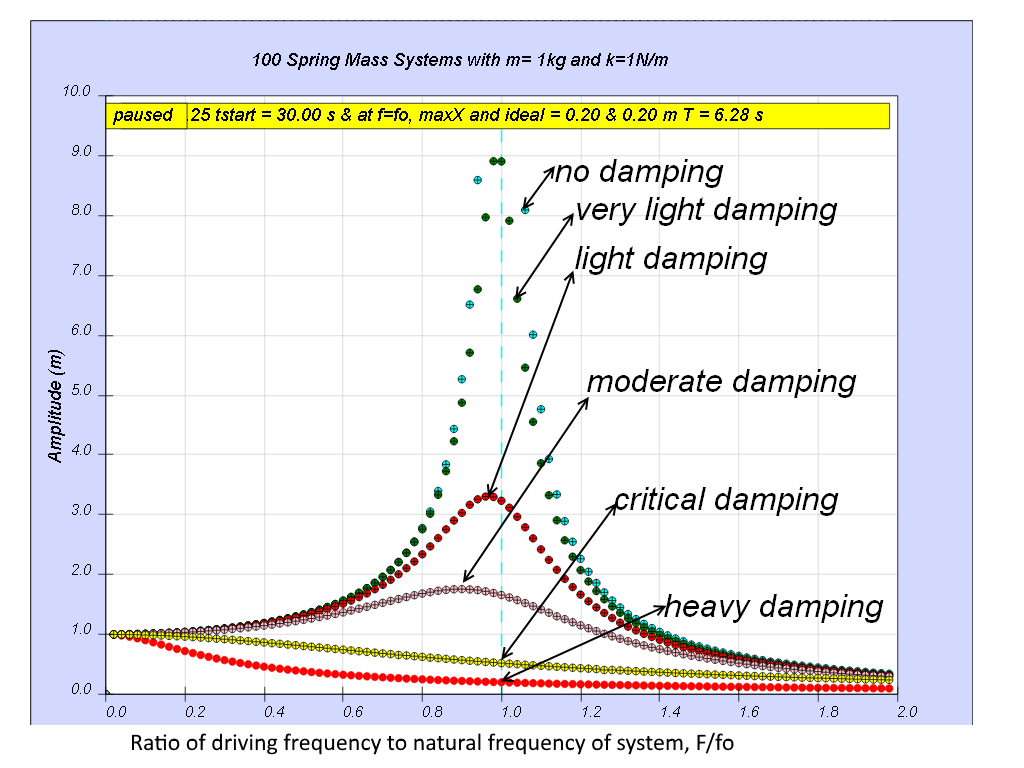
1.7.4.1 Case 1: b=0 no damping.

All 100 spring mass systems oscillates forever without coming to rest. Notice when the ratio of driving frequency to natural frequency f_o of the oscillating system  f/fo = 1  maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude (extended beyond 10).  This phenomenon is called resonance. 

  

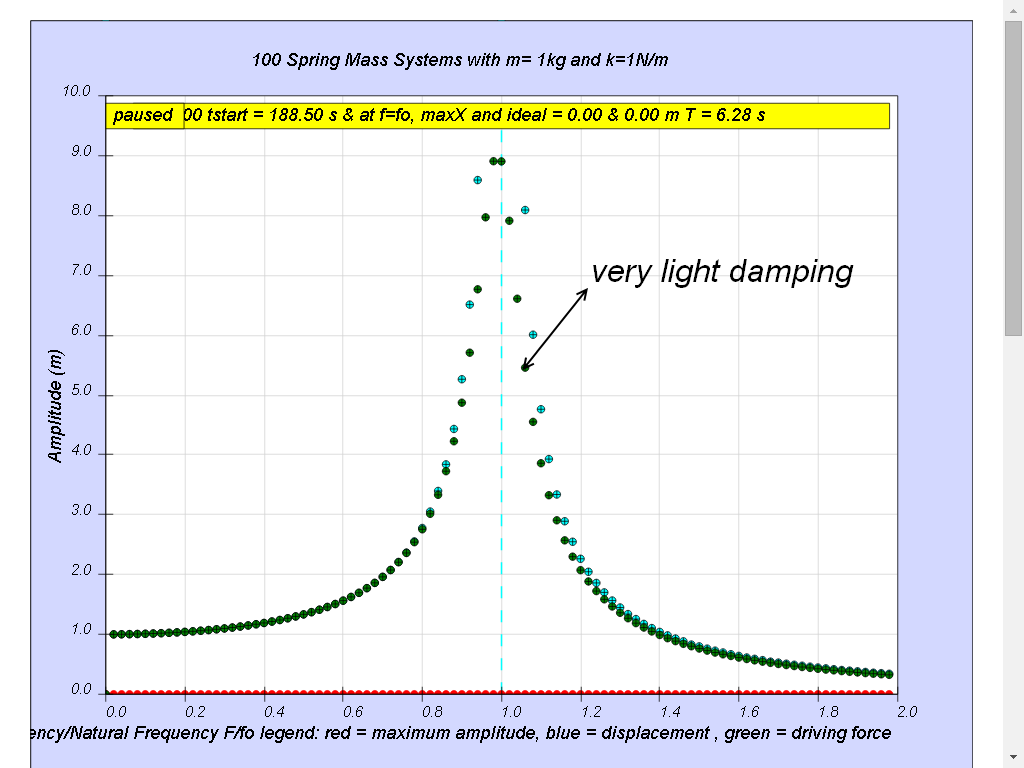
1.7.4.2 Case 2: b=0.1 very light damping

Notice when the ratio of driving frequency to natural frequency f_o of the oscillating system  f/fo = 1  maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude (equal 10 m).  This phenomenon is called resonance. 

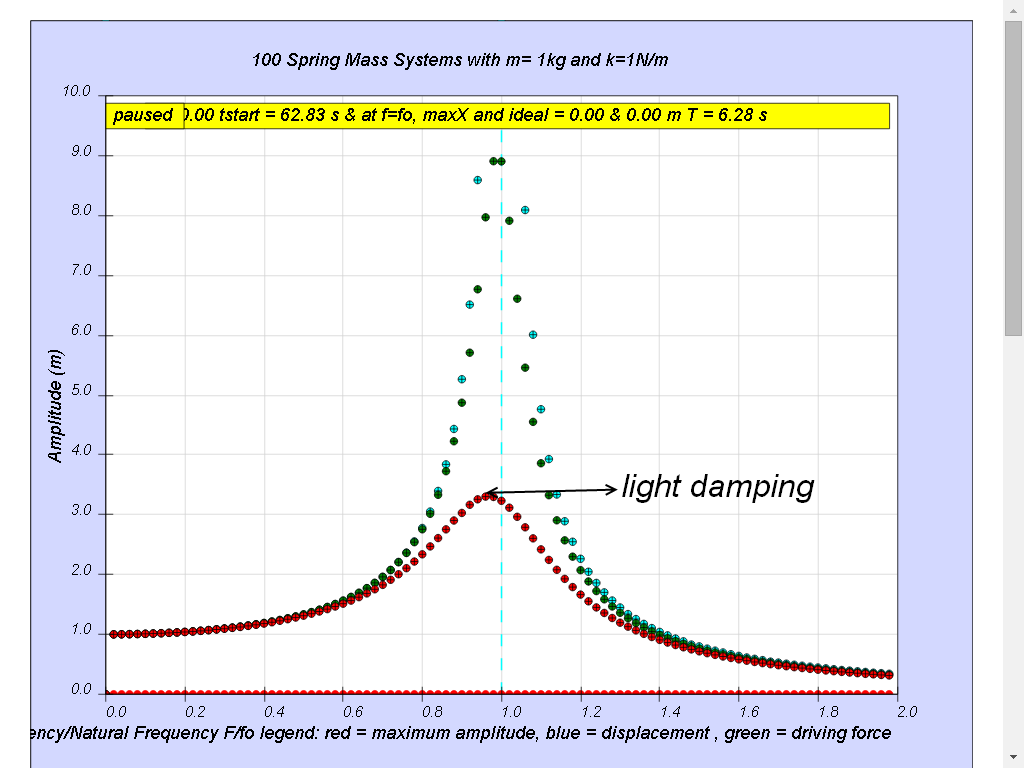
1.7.4.3 Case3: b=0.3 light damping

Notice when the ratio of driving frequency to natural frequency f_o of the oscillating system  f/fo slightly less than 1,  maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude (about 3.3).  This phenomenon is called resonance. 

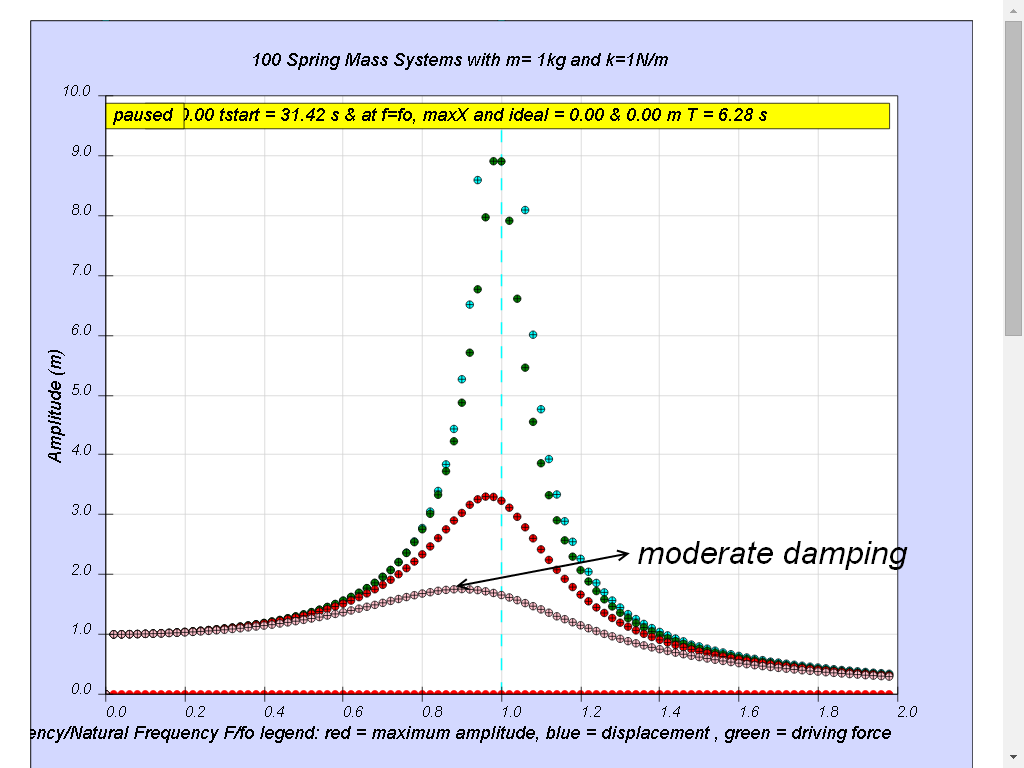
1.7.4.4 Case4: b =0.6 moderate damping

Notice when the ratio of driving frequency to natural frequency f_o of the oscillating system  f/fo slightly less than 1 about 0.9 in this case,  maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude (about 1.8).  This phenomenon is called resonance.

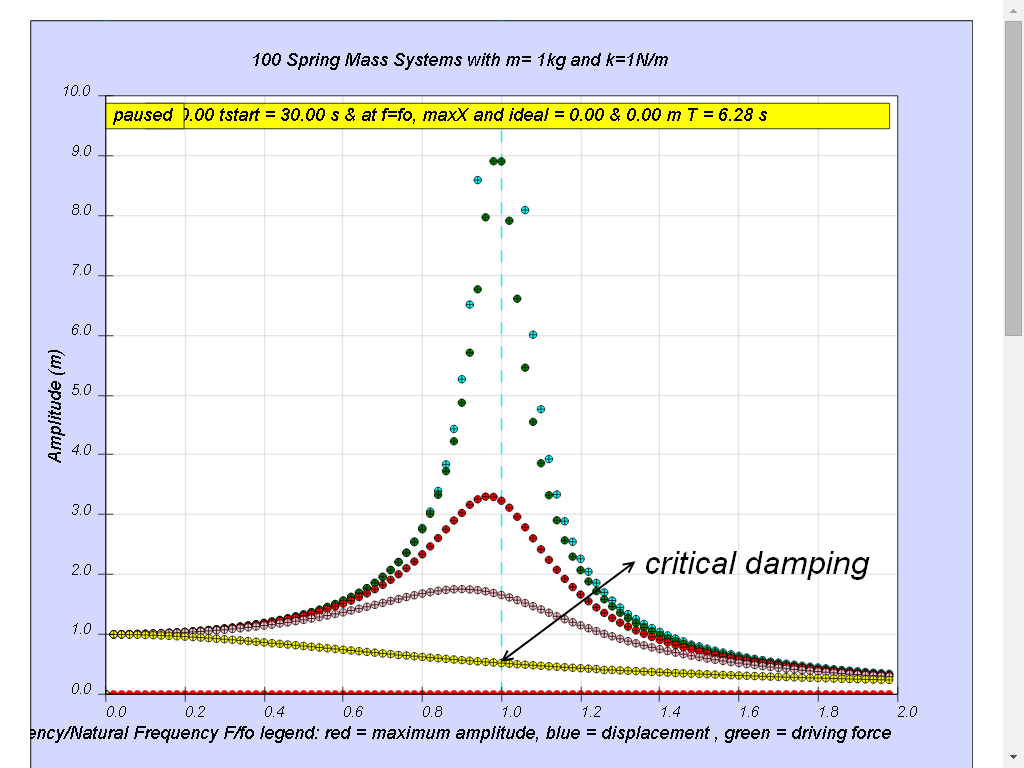
1.7.4.5 Case5: b = 2.0 critical damping

Notice the resonance does not occur anymore. 

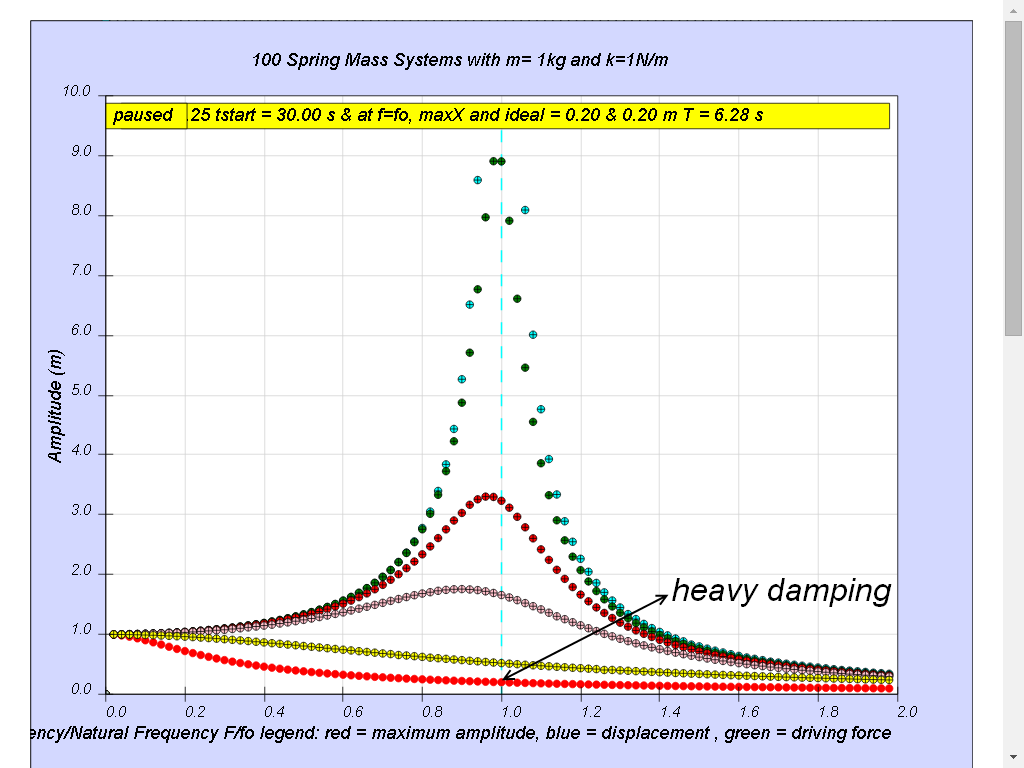
1.7.4.6 Case6: very heavy damping

Notice the resonance does not occur anymore. 

1.7.5 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/88

1.7.6 YouTube explanation:

http://youtu.be/tl4hfZ3TR6U

1.7.7 YouTube

http://youtu.be/LV_UuzEznHs  How is this video related to resonance? Hint: consider the shaking support table is the driver, moving an driver frequency f, and the natural frequency of the left, middle and right structure each have their own natural frequency f₀₁, f₀₂, f₀₃.

http://youtu.be/17tqXgvCN0E This video shows the oscillating of a wine glass by playing sound (driver) at its(wine glass) natural frequency resulting in resonance.Note stroboscope is used to observe the resonant effect better.

http://youtu.be/M8ztJGT6AHc Marina Bay Sands cantilever - real world application of resonance.
Note that video ends at 5.40 min.

http://youtu.be/1yaqUI4b974 Though not really in A-Level Physics syllabus, the experiment shows the beauty of physics where sound at certain frequencies can produce detailed 2 dimensions patterns of sands that tends to be deposited at positions where the displacement is zero and areas of resonances (high amplitudes) the sand tend to be disturbed and move away from these position, resulting in the detailed patterns of sands.

 

Translations

Code	Language		Translator	Run

Credits

weelookang@gmail.com; leetatleong

Briefing Document: Student Learning Space Resonance type 0 HTML5 Applet Simulation Model

This document summarizes the key themes and ideas presented in the provided excerpt from the "Student Learning Space Resonance type 0 HTML5 Applet Simulation Model" resource. The resource focuses on demonstrating and explaining the phenomenon of resonance in an oscillatory system using an interactive computer model.

Main Themes:

• Resonance: The core concept explored is resonance, specifically how it occurs when the driving frequency of a periodic force matches the natural frequency of an oscillating system.
• Driving Frequency & Natural Frequency: The relationship between these two frequencies is critical. "When the driving frequency f is close to or equal to the natural frequency fo of the oscillating system, maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude. This phenomenon is called resonance."
• Damping: The resource investigates the impact of damping on resonance, showing how increasing damping reduces the amplitude of oscillation at resonance and eventually eliminates the resonance phenomenon altogether.
• Interactive Simulation: The resource highlights the use of a computer model (HTML5 Applet) to visualize and explore resonance. The model allows users to manipulate parameters and observe the resulting behavior of the system.
• Open Educational Resource: The resource is presented as an open educational resource, emphasizing its accessibility and potential for use in educational settings.

Key Ideas and Facts:

• Definition of Resonance: Resonance occurs when the driving frequency of a periodic force matches the natural frequency of an oscillating system, resulting in maximum energy transfer and large amplitude oscillations.
• Impact of Damping:No Damping (b=0): The system oscillates forever without coming to rest. Maximum amplitude is achieved at f/fo = 1.
• Light Damping (b=0.1 & b=0.3): Resonance still occurs, but the maximum amplitude is reduced. The peak of the resonance curve may shift slightly.
• Moderate Damping (b=0.6): Resonance still occurs, but the maximum amplitude is further reduced.
• Critical & Heavy Damping (b=2.0 and Very Heavy): Resonance no longer occurs. The system does not oscillate significantly in response to the driving force.
• Model Functionality: The computer model allows users to "generate a similar data representation when using the instruction found on the html below the model." This implies the model can be used for quantitative analysis and data collection.
• Real-World Examples: The resource links to YouTube videos showcasing real-world examples of resonance, including:
• A shaking support table influencing structures with different natural frequencies.
• A wine glass oscillating due to sound at its natural frequency.
• The Marina Bay Sands cantilever structure.
• Patterns formed by sand on a vibrating plate.
• Accessibility: The resource includes links to apps and other related materials, such as an iCTLT e-poster presentation.

Quotes:

• "When the driving frequency f is close to or equal to the natural frequency fo of the oscillating system, maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude. This phenomenon is called resonance."
• "Notice when the ratio of driving frequency to natural frequency fo of the oscillating system f/fo = 1 maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude (extended beyond 10). This phenomenon is called resonance." (Case 1: b=0 no damping)
• "Notice the resonance does not occur anymore." (Case 5: b = 2.0 critical damping and Case 6: Very Heavy Damping)

Overall Significance:

This resource provides a valuable tool for understanding and visualizing the concept of resonance. The interactive simulation, coupled with real-world examples, can enhance student learning and engagement. The exploration of damping adds another layer of complexity, demonstrating how real-world factors can affect resonant behavior. The availability as an open educational resource makes this information widely accessible for educators and learners.

 

Resonance: A Study Guide

Quiz

1. What is resonance, in the context of oscillating systems?
2. What is the relationship between the driving frequency and the natural frequency of an oscillating system during resonance?
3. According to the simulation, what happens to the amplitude of the oscillating system when resonance occurs?
4. What is damping, and how does it affect resonance?
5. In the simulation, what value of 'b' (damping coefficient) causes resonance to no longer occur?
6. Give a real-world example of resonance.
7. How does the simulation demonstrate the transfer of energy from the driver to the oscillating system?
8. Explain why maximum amplitude (extended beyond 10) occurs when b=0.
9. How does light damping affect the ratio of driving frequency to natural frequency (f/fo) at which resonance occurs, compared to no damping?
10. What are some of the educational resources linked with this simulation?

Quiz Answer Key

1. Resonance is a phenomenon where an oscillating system vibrates with maximum amplitude when the frequency of a periodic force (driving frequency) is close to or equal to the system's natural frequency.
2. During resonance, the driving frequency is close to or equal to the natural frequency of the oscillating system.
3. During resonance, the amplitude of the oscillating system is at its maximum.
4. Damping is a force that opposes motion and dissipates energy from the oscillating system. It reduces the amplitude of oscillations and can prevent resonance from occurring.
5. According to the simulation, resonance no longer occurs when b = 2.0 (critical damping) or with very heavy damping.
6. Examples include a wine glass shattering when a sound is played at its natural frequency, or the Tacoma Narrows Bridge collapse due to wind-induced oscillations.
7. The simulation demonstrates energy transfer through the amplitude of the spring mass system, which is at its highest when the driving frequency matches the natural frequency.
8. With no damping, the system loses no energy, allowing the amplitude to grow indefinitely when the driving frequency matches the natural frequency (f/fo = 1), leading to amplitude values exceeding 10.
9. Light damping (e.g., b=0.3 or b=0.6) causes resonance to occur when the ratio of driving frequency to natural frequency (f/fo) is slightly less than 1.
10. Some of the educational resources that are linked with this simulation include YouTube videos, iCTLT e-poster presentations and videos, and links to apps on the Google Play store.

Essay Questions

1. Discuss the relationship between driving frequency, natural frequency, and damping in the phenomenon of resonance. Use examples from the simulation and real-world scenarios to illustrate your points.
2. Analyze the effect of different damping coefficients on the resonance curve (amplitude vs. driving frequency) of an oscillating system. How does increasing damping affect the peak amplitude and the frequency at which resonance occurs?
3. Evaluate the use of the "Student Learning Space Resonance type 0 HTML5 Applet Simulation Model" as an educational tool for teaching the concept of resonance. What are its strengths and weaknesses?
4. Explore the real-world applications of resonance, both beneficial and detrimental. Provide specific examples and explain the physics principles involved.
5. Explain how resonance differs when damping is absent, very light, light and moderate and how heavy damping affects the oscillating system.

Glossary of Key Terms

• Resonance: The phenomenon where an oscillating system experiences maximum amplitude when the driving frequency is close to or equal to its natural frequency.
• Driving Frequency (f): The frequency of the external force applied to an oscillating system.
• Natural Frequency (fo): The frequency at which an oscillating system will vibrate freely when disturbed.
• Amplitude: The maximum displacement of an oscillating system from its equilibrium position.
• Damping (b): A force that opposes motion and dissipates energy from an oscillating system, causing the amplitude to decrease over time.
• Oscillating System: A system that exhibits periodic motion, such as a spring-mass system or a pendulum.
• Periodic Force: A force that repeats itself over time, often used to drive or excite an oscillating system.
• Critical Damping: The level of damping that returns the system to equilibrium as quickly as possible without oscillating.

{accordionfaq faqid=accordion3 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}

 Apps

https://play.google.com/store/apps/details?id=com.ionicframework.shm24app916792&hl=en

iCTLT e-poster video 2 minutes

1. Version 30 March 2016 Minister
2. Version 17 March 2016   
3. Version 14 March 2016 
4. Version February  

iCTLT e-poster presentation

   https://docs.google.com/a/moe.gov.sg/presentation/d/10ejVJIyXA8u2DILcEbJ-RACLxoPvvqrTiC02fqfNJIc/edit?usp=sharing

 https://docs.google.com/presentation/d/1g7U7dwjxdQ8k9Z62AzXEQCM3K0NcNqvxCXugOXv-qpA/edit#slide=id.p4

 https://docs.google.com/presentation/d/1lSySjVaEDlIRBniKie2xyCu3B6go2AjJqe00D_vUr5Q/edit#slide=id.g10abfba361_0_25

 

Video

https://youtube.com/shorts/te4-qw7DW6M?si=y6FhRhWu2kDAO0l3   

FAQ on Resonance and Oscillations

• What is resonance?
• Resonance is a phenomenon that occurs when an oscillating system is driven by a periodic force with a frequency close to or equal to the system's natural frequency. At resonance, energy is transferred very efficiently from the driver to the oscillating system, causing the system to vibrate with maximum amplitude.
• What is "natural frequency" in the context of resonance?
• The natural frequency (f₀) of an oscillating system is the frequency at which the system will oscillate freely if disturbed from its equilibrium position. It's determined by the physical properties of the system, such as mass and stiffness (in the case of a spring-mass system).
• How does the driving frequency relate to the natural frequency in achieving resonance?
• Maximum resonance occurs when the driving frequency (f) of the periodic force is close to or exactly matches the natural frequency (f₀) of the oscillating system (i.e., f/f₀ ≈ 1). This condition allows for the most efficient transfer of energy, leading to the largest amplitude of oscillation.
• What effect does damping have on resonance?
• Damping is the dissipation of energy from an oscillating system, usually due to friction. Light damping allows resonance to occur, but with a finite amplitude at the resonant frequency. As damping increases, the amplitude at resonance decreases, and the resonant frequency may shift slightly. With critical or heavy damping, resonance may no longer occur at all; instead, the system returns to equilibrium without significant oscillation.
• How can the Student Learning Space Resonance applet be used to explore resonance?
• The Student Learning Space Resonance applet simulates spring-mass systems with varying degrees of damping, which allows the relationship between driving frequency, natural frequency, damping, and amplitude of oscillation to be visually explored. The applet allows users to change the damping coefficient and observe the resulting changes in resonant behavior.
• Can you provide real-world examples of resonance?
• Yes. Examples include:
• A vibrating wine glass shattered by sound waves matching its natural frequency.
• The potential for structural damage to buildings like the Marina Bay Sands cantilever if vibrations match their natural frequencies.
• Where can I find interactive simulations to further explore resonance?
• The provided text lists several interactive HTML5 applets and simulations related to oscillations, waves, and related concepts, such as the "Student Learning Space Resonance type 0 HTML5 Applet Simulation Model." The resources can be found on the Open Educational Resources / Open Source Physics @ Singapore platform, specifically iwant2study.org.
• What other educational resources are available on the Open Educational Resources / Open Source Physics @ Singapore platform?
• The platform provides numerous interactive simulations, games, and learning resources covering various topics in physics and mathematics. These resources include simulations of mechanics, electromagnetism, optics, and more. There are also math tools, virtual labs, and interactive quizzes for students.