About

1.2.11 Example: Spring-mass system

 
A mass suspended from a spring, displaced vertically and released to move freely to produce up and down motion

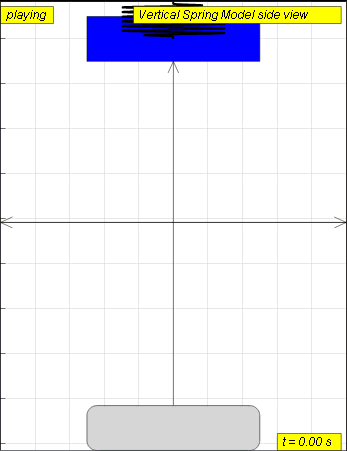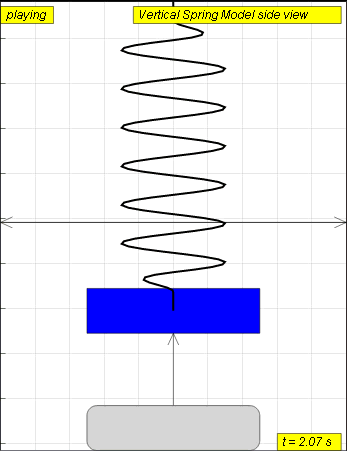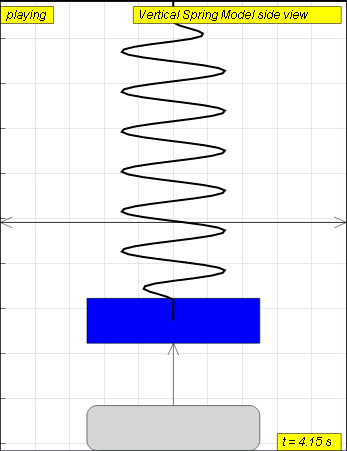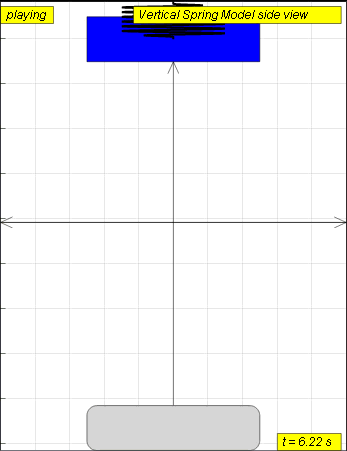
The model view of a mass suspended from a spring, displaced vertically and released to move freely to produce up and down motion with right panel showing the displacement, velocity and acceleration. 

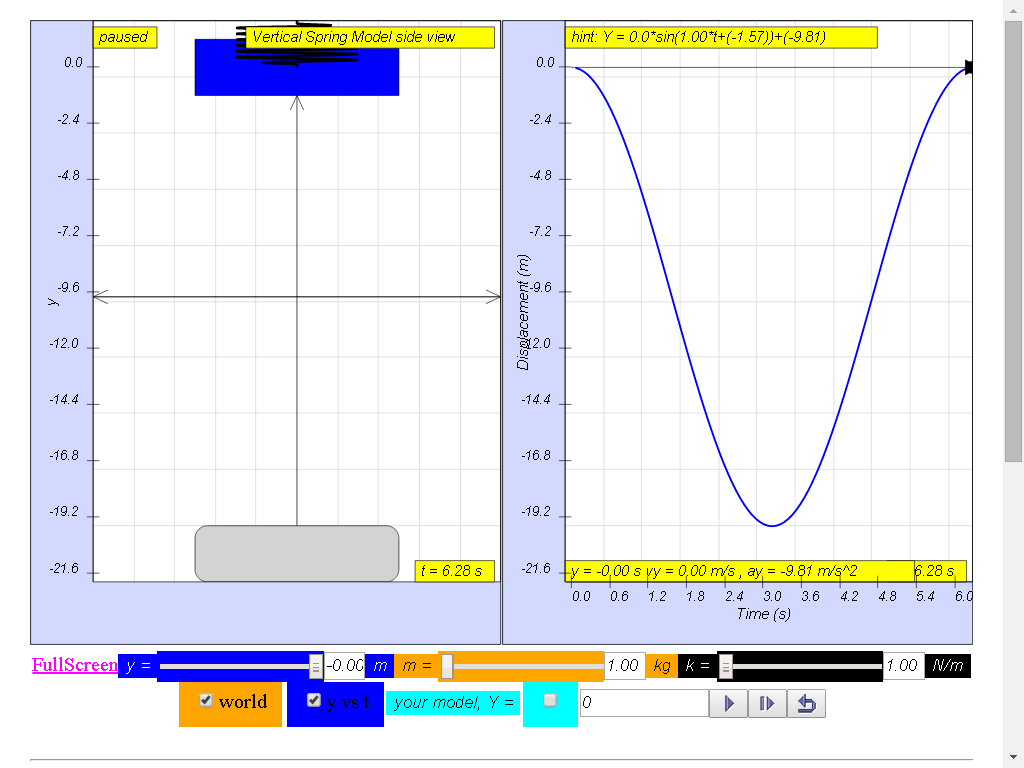
Q1: under what conditions would this vertical spring mass system’s motion be not well modeled as a simple harmonic motion?

H1: the model assumes the restoring force by the spring is F = -ky, it is always correct for any magnitude of oscillation y in real springs. Is it always valid in the real spring motion when the spring is hyper extending beyond the linear limits of Hooke's Law ?

Q2: change the simulation y=0 m and Play the model. In the your model Y = _________, suggest your own suitable model that can describe the motion y.

Q3: in this same motion, propose the velocity and acceleration model(s)

Q4: carry out some other conditions, verify that the general equations for displacments if can be model by Y = Y₀sin(ωt+φ)+Y_shift where the usual symbols have the usual meaning. Hence or otherwise, Suggest with reasons, the meaning of Y₀ , ω , φ , and Y_shift.

Q5: similarly, suggest whether the model(s) for velocity, v_Y =ωY₀cos(ωt+φ) and

a_Y = - ω²Y₀sin(ωt+φ). Test them out using an example of your choice.

1.2.11.1 YouTube

http://youtu.be/P-Umre5Np_0 MIT Physics Demo -- Spray Paint Oscillator. A can of spray paint is attached to a spring oscillator. A roll of paper is run past the oscillating can. The result is a sine wave - http://en.wikipedia.org/wiki/Sine_wave - on the paper.Watch the original video on MIT TechTV - http://techtv.mit.edu/videos/803-spray-paint-oscillator

1.2.11.2 Tracker activity:

http://weelookang.blogspot.sg/2012/08/tracker-modeling-in-spring-mass-system.html

1.2.11.3 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/90

 

Translations

Code	Language		Translator	Run

Credits

weelookang@gmail.com

Briefing Document: Student Learning Space Force Oscillation JavaScript HTML5 Applet Simulation Model

1. Overview:

This document details a JavaScript HTML5 applet simulation model for illustrating forced oscillations, specifically focusing on a spring-mass system. It's part of the Open Educational Resources / Open Source Physics @ Singapore initiative. The resource includes an interactive simulation, embedded questions to guide student exploration, and links to related resources such as YouTube videos and Tracker activities. It aims to help students understand simple harmonic motion and its deviations in real-world scenarios.

2. Main Themes and Key Ideas:

• Interactive Simulation of Forced Oscillations: The core of the resource is an interactive simulation of a mass-spring system undergoing forced oscillation. The provided code snippet shows how the simulation can be embedded into a webpage using an iframe.
• <iframe width="100%" height="100%" src="https://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM161SLS_forcedoscillation/SHM161SLS_forcedoscillation_Simulation.xhtml " frameborder="0"></iframe>
• Exploration of Simple Harmonic Motion (SHM): The simulation allows students to explore the relationship between displacement, velocity, and acceleration in SHM.
• Limitations of SHM: A key focus is on understanding the conditions under which the SHM model breaks down. For example, one question directly asks: "Q1: under what conditions would this vertical spring mass system’s motion be not well modeled as a simple harmonic motion?" The answer (H1) highlights the limitations of Hooke's Law: "the model assumes the restoring force by the spring is F = -ky, it is always correct for any magnitude of oscillation y in real springs. Is it always valid in the real spring motion when the spring is hyper extending beyond the linear limits of Hooke's Law ?" This prompts students to consider the validity of the model in extreme scenarios.
• Guided Inquiry-Based Learning: The resource uses a question-and-answer format to encourage students to investigate and analyze the simulation's behavior. Questions include:
• Developing models for displacement, velocity, and acceleration (Q2, Q3, Q4, Q5).
• Verifying general equations for displacement. "carry out some other conditions, verify that the general equations for displacments if can be model by Y = Y0sin(ωt+φ)+Yshift where the usual symbols have the usual meaning. Hence or otherwise, Suggest with reasons, the meaning of Y0 , ω , φ , and Yshift."
• Suggesting suitable models for velocity and acceleration, and testing them using examples. "similarly, suggest whether the model(s) for velocity, vY =ωY0cos(ωt+φ) and aY = - ω2Y0sin(ωt+φ). Test them out using an example of your choice."
• Supplementary Resources: Links are provided to a MIT Physics Demo on YouTube ("http://youtu.be/P-Umre5Np_0 MIT Physics Demo -- Spray Paint Oscillator") showing a real-world analogue and to a Tracker activity ("http://weelookang.blogspot.sg/2012/08/tracker-modeling-in-spring-mass-system.html") for further analysis.
• Exploration of Factors Affecting Period: Another interactive element allows users to "Explore some factors that affect the period of a spring," such as gravity, spring constant, starting distance, and mass. It also prompts comparison with pendulum motion and the effect of damping.
• Pendulum on a Spring Exploration: Another simulation allows for the exploration of "the motion of a pendulum on a spring," encouraging students to distinguish and compare spring and pendulum motion patterns and the energy transfer between them.

3. Target Audience:

The resource appears designed for secondary/high school or introductory college physics students studying oscillations, SHM, and the limitations of idealized models.

4. Potential Uses:

• Interactive classroom demonstration.
• Student-led exploration and experimentation.
• Homework assignment or lab activity.
• Supplement to textbook material on oscillations.

5. Key Takeaways:

• The resource provides a hands-on, visual way to understand the concepts of forced oscillations and SHM.
• It emphasizes the importance of considering the assumptions and limitations of physical models.
• The guided inquiry approach encourages critical thinking and problem-solving skills.
• The integration of external resources enhances the learning experience.
• The simulation is embedded directly into the site allowing for ease of distribution.

6. Related Resources on the Site:

The document also lists a large number of other simulation models covering a wide range of physics and mathematics topics, from mechanics and electromagnetism to optics and quantum physics. Many simulations are also virtual labs with factors affecting Transpiration. There are also many simulations on quizzes. Many are created using EJS (Easy Java Simulations). The site also highlights awards and recognition received for its contributions to open educational resources.

Spring-Mass System Simulation Study Guide

Quiz: Short Answer Questions

1. Under what conditions would a vertical spring-mass system not be well-modeled as simple harmonic motion (SHM)?
2. If you change the simulation to y = 0 m and play the model, what does the Y value represent in the context of the simulation?
3. Propose a model for the velocity and acceleration of the spring-mass system. Explain the relationship between displacement, velocity, and acceleration in this model.
4. What are the meanings of Y0, ω, φ, and Yshift in the general equation for displacement, Y = Y0sin(ωt+φ)+Yshift, when applied to the spring-mass system?
5. Explain the relationship between displacement, velocity and acceleration model(s) vY =ωY0cos(ωt+φ) and aY = - ω2Y0sin(ωt+φ).
6. How can you use the simulation to explore the effects of gravity, spring constant, starting distance, and mass on the period of the oscillation?
7. How does the damping slider affect the period of oscillation in the simulation, and why?
8. What happens to the energy of the system when damping is applied to the simulation?
9. How can you distinguish the spring motion pattern from the pendulum motion pattern?
10. Under what conditions does the energy switch between back and forth and up and down in the simulation?

Quiz Answer Key

1. The spring-mass system would not be well-modeled as SHM when the restoring force of the spring is no longer proportional to the displacement. This occurs when the spring is stretched or compressed beyond its elastic limit, violating Hooke's Law, or when damping forces are significant.
2. If you change the simulation to y = 0 m and play the model, the Y value represents the initial displacement from the equilibrium position. It sets the starting point of the oscillation, determining the amplitude of the motion if no other initial velocity is applied.
3. The velocity model is the time derivative of the displacement and acceleration model is the time derivative of the velocity. When displacement is at a maximum (positive or negative), velocity is zero and the acceleration is at its maximum, but in the opposite direction of the displacement.
4. Y0 is the amplitude of the oscillation (the maximum displacement from the shifted equilibrium position), ω is the angular frequency (related to the period of oscillation), φ is the phase constant (determining the initial position at t=0), and Yshift is the vertical shift of the equilibrium position.
5. The velocity is proportional to the angular frequency and the cosine of the phase angle, representing the rate of change of displacement, while acceleration is proportional to the negative square of the angular frequency and the sine of the phase angle, representing the rate of change of velocity. Acceleration is opposite in sign to the displacement, indicating that it acts as a restoring force.
6. You can use the simulation by systematically changing each parameter (gravity, spring constant, starting distance, mass) individually while keeping others constant. Observe the changes in the graph of height vs. time to determine how each parameter affects the period of the oscillation.
7. The damping slider introduces a frictional force that opposes the motion, causing the amplitude of the oscillation to decrease over time. Damping does not significantly change the period itself but affects the rate at which the oscillation decays.
8. When damping is applied, the energy of the system is gradually dissipated due to the work done by the damping force. This energy is converted into heat, causing the oscillations to decrease in amplitude and eventually stop.
9. You can distinguish the spring motion pattern from the pendulum motion pattern by analyzing the graphs. The spring motion (up and down) typically shows a sinusoidal pattern, while the pendulum motion (back and forth) is also sinusoidal, but with a phase difference, and their combination can create Lissajous curves.
10. The energy switches between back and forth and up and down depending on the initial conditions and the relationship between the spring constant, rod length, mass, and gravity. When the frequencies of the pendulum and spring oscillations are close, energy can transfer between the two modes.

Essay Questions

1. Discuss the limitations of modeling a real-world spring-mass system using simple harmonic motion. Include factors such as damping, non-linear spring behavior, and external forces.
2. Explain how the concepts of potential and kinetic energy are manifested in the spring-mass system simulation. Describe how these energies transform throughout one complete cycle of oscillation, both with and without damping.
3. Describe the relationship between the simulation, the YouTube video of the spray paint oscillator, and the Tracker activity. How can these resources complement each other in understanding simple harmonic motion?
4. How could you use the simulation to design an experiment to determine the spring constant of a real-world spring? Discuss the steps involved, potential sources of error, and how to minimize them.
5. Compare and contrast the motion of a simple pendulum with that of a spring-mass system. What parameters influence their respective periods, and what are the key differences in their behavior?

Glossary of Key Terms

• Simple Harmonic Motion (SHM): A type of periodic motion where the restoring force is directly proportional to the displacement and acts in the direction opposite to that of displacement.
• Hooke's Law: A law stating that the force needed to extend or compress a spring by some distance is proportional to that distance. Expressed as F = -kx, where F is the force, k is the spring constant, and x is the displacement.
• Spring Constant (k): A measure of a spring's stiffness; the higher the spring constant, the stiffer the spring.
• Amplitude (Y0): The maximum displacement of an oscillating object from its equilibrium position.
• Angular Frequency (ω): A measure of how rapidly an object is oscillating, expressed in radians per second. Related to frequency (f) and period (T) by ω = 2πf = 2π/T.
• Phase Constant (φ): A constant that determines the initial position of an oscillating object at time t=0.
• Period (T): The time required for one complete cycle of oscillation.
• Frequency (f): The number of cycles of oscillation per unit time, typically measured in Hertz (Hz).
• Damping: The dissipation of energy in an oscillating system, leading to a decrease in amplitude over time.
• Equilibrium Position: The position of an object when it is at rest and no net force is acting on it.
• Restoring Force: A force that acts to return an object to its equilibrium position.
• Potential Energy: The energy stored in an object due to its position or configuration. In a spring-mass system, it is the energy stored in the spring when it is stretched or compressed.
• Kinetic Energy: The energy of motion. In a spring-mass system, it is the energy of the mass as it moves.

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM161/SHM161_Simulation.xhtml

Other Resources

 

 

FAQ on Spring-Mass System Simulations

• Q1: Under what conditions is the spring-mass system simulation not well-modeled as Simple Harmonic Motion (SHM)?
• A1: The simulation assumes the restoring force of the spring is perfectly described by Hooke's Law (F = -ky), which implies a linear relationship between force and displacement. In reality, Hooke's Law has limitations. If the spring is stretched or compressed beyond its elastic limit, the restoring force will no longer be proportional to the displacement, and the motion will deviate from SHM. This is especially true when the spring is hyper-extending beyond the linear limits.
• Q2: How does initial displacement affect the modeled motion?
• A2: The initial displacement (Y=0 in the given scenario) determines the starting point of the oscillation. A suitable model to describe the motion y would involve a sinusoidal function such as Y = Y0sin(ωt+φ)+Yshift, where Y0 is the amplitude, ω the angular frequency, φ the phase, and Yshift the vertical shift in the equilibrium position.
• Q3: What are appropriate models for velocity and acceleration in this simulation?
• A3: Assuming the displacement can be modeled by Y = Y0sin(ωt+φ)+Yshift, the corresponding models for velocity and acceleration are:
• Velocity (vY): vY = ωY0cos(ωt+φ)
• Acceleration (aY): aY = - ω2Y0sin(ωt+φ)
• Q4: What do the parameters Y0, ω, φ, and Yshift represent in the displacement equation Y = Y0sin(ωt+φ)+Yshift?
• A4: These parameters define the characteristics of the oscillating motion:
• Y0: The amplitude of the oscillation. It represents the maximum displacement from the equilibrium position (or shifted equilibrium position).
• ω: The angular frequency, determining the rate of oscillation. It's related to the period (T) by ω = 2π/T.
• φ: The phase constant or phase shift, specifying the initial position of the oscillating mass at time t=0. It determines whether the oscillation starts at its maximum displacement, equilibrium, or somewhere in between.
• Yshift: The vertical shift of the equilibrium position of the mass-spring system. This accounts for the spring being extended at equilibrium due to gravity.
• Q5: How can the proposed models for velocity and acceleration be tested within the simulation?
• A5: To test the velocity and acceleration models, set specific conditions (e.g., mass, spring constant, initial displacement) within the simulation. Observe the displacement, velocity, and acceleration curves. By comparing these curves to the predictions made by the equations vY = ωY0cos(ωt+φ) and aY = - ω2Y0sin(ωt+φ), you can validate whether the models accurately represent the simulated motion. Pay attention to the phase relationships and amplitudes.
• Q6: How can the period of the spring-mass system be determined using the simulation?
• A6: Run the simulation and observe the graph of the mass's height over time. The period (T) is the time it takes for the mass to complete one full oscillation (one up-and-down cycle). You can read the period directly from the graph.
• Q7: How do different factors (gravity, spring constant, starting distance, mass, damping) affect the period of the spring-mass system?
• A7:
• Gravity: While gravity affects the equilibrium position (Yshift in the model), it doesn't directly affect the period of oscillation in an ideal spring-mass system.
• Spring Constant (k): A higher spring constant increases the restoring force, leading to a shorter period (faster oscillations). The period is inversely proportional to the square root of k.
• Starting Distance (Initial Displacement): The starting distance (initial displacement) only affects the amplitude of the oscillation (Y0) and doesn't affect the period.
• Mass (m): A larger mass increases the inertia of the system, resulting in a longer period (slower oscillations). The period is directly proportional to the square root of m.
• Damping: Damping doesn't change the period of oscillation, but it reduces the amplitude over time, causing the oscillations to die out.
• Q8: How does the motion of a pendulum on a spring differ from a simple spring-mass system or a simple pendulum?
• A8: A pendulum on a spring combines the motion of a vertical spring-mass system (oscillating up and down) and a pendulum (swinging back and forth). The interaction between these motions can produce complex patterns. Energy can switch between the spring motion and pendulum motion. The periods of the spring and pendulum motions are generally different. Changing variables (gravity, rod length, mass, spring constant) alters the relative frequencies of the two motions, leading to different patterns of energy transfer and overall motion.