Translations

Code	Language		Translator	Run

Credits

weelookang@gmail.com

Briefing Document: Vector Component Simulation

1. Overview

This document analyzes a resource from Open Educational Resources / Open Source Physics @ Singapore, specifically focusing on a "Student Learning Space quiz type 2 resultant displacement QUIZ JavaScript HTML5 Applet Simulation Model." This interactive simulation is designed to help students understand and calculate vector components, a fundamental concept in physics and other sciences. The resource emphasizes the decomposition of vectors into horizontal (x) and vertical (y) components.

2. Key Concepts

• Vectors: The resource clearly defines vectors as quantities possessing both magnitude and direction. It provides examples like displacement, velocity, acceleration, and force. The document states, "A vector is a quantity that has both magnitude and direction."
• Scalar: Quantities that only have magnitude are considered scalars, this isn't mentioned explicitly but is implied when the document explains "state what is meant by scalar and vector (how to resolve) quantities and give common examples of each"
• Vector Decomposition: A central idea is that vectors can be "resolved" or broken down into components. Specifically, the resource focuses on resolving vectors into components along the x and y axes. As stated, "a useful mathematical trick will be employed to transform the vector into two parts with each part being directed along the coordinate axes." The simulation allows users to explore how changes to the x and y components affect the overall vector.
• Mathematical Representation: The document gives the mathematical equations for calculating vector components:
• ( A_{x} = A cos( \theta) ) (x-component)
• ( A_{y} = A sin( \theta) ) (y-component)
• Magnitude: ( |A| = \sqrt {( A_{x}^{2}+A_{y}^{2})} )
• Angle: ( \theta = tan^{-1} (\frac {A_{y}}{A_{x}}) )
• Not All Quantities with Magnitude and Direction Are Vectors: The resource explicitly notes that some quantities, like angular displacement and electric current, do have magnitude and direction but are NOT vectors because they "fail to follow the rules of vector addition."
• "Examples of quantities that have magnitude and direction but fail to follow the rules of vector addition: Angular displacement and electric current. Consequently, these are not vectors."

3. Simulation Features and Functionality

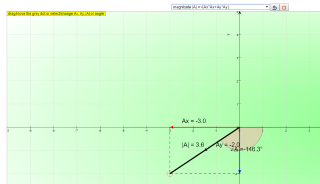
• Random Vector Generation: The simulation starts by generating a random vector A, defined by its magnitude (|A|) and angle (θ) with respect to the x-axis. "click reset to generate a new random vector A of length |A| at an angle of theta to the positive x axis."
• Component Calculation: Students are expected to use the provided formulas to calculate the x-component (Ax) and y-component (Ay) of the vector. "use the formula Ax = |A|cos(theta) to find the x direction component Ax."
• Interactive Exploration: The simulation includes checkboxes for Ax and Ay, and a PLAY button that animates the effect of changing these components individually. This allows the student to directly observe the impact of vector components on the overall vector's direction and magnitude. This interactive feature is a key element in helping to solidify understanding. "when Ax is selected, the PLAY button animates the effects of changing Ax alone."
• User-Defined Values: Users can input their own values for |A| and θ to explore and test their understanding with a particular vector. "this model can be used to calculate any length |A| by keying in the values such as |A| =500 and theta = 63 degrees."
• Self-Testing: The simulation enables a self-assessment, as students calculate the x and y components and then compare them to the displayed values. "test yourself whether you have enough practice calculating Ax and Ay."
• Degrees to Radians: The simulation allows for the use of degrees as the input value for the angle of a vector but internally stores and calculates vector components using radians.
• ( \theta = ( \theta_{degree} )( \frac{\pi}{180}) )

4. Educational Objectives

The learning goals outlined for the simulation are:

• To understand the difference between scalar and vector quantities.
• "(e) state what is meant by scalar and vector (how to resolve) quantities and give common examples of each"
• To be able to calculate vector components.
• "(f) calculate vector by means of components"

5. Other Relevant Features

• Links to Additional Resources: The page also includes links to similar applets and simulations, offering a variety of tools for further exploration, including "Example JavaScript Model Ill 3.1: Vector Decomposition" and a Geogebra applet.
• Credits: The document provides credits to the various developers and contributors to the project, including lookang, Fu-Kwun, Andreu Glasmann, Wolfgang Christian, and Mario Belloni.
• Embeddable: The document describes how the simulation can be embedded on webpages, increasing its accessibility to students using different digital learning tools. ""
• Offline Use: The document provides a direct download link so the simulation can be used offline. "offline use: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_horizontalvertical.zip"

6. Related Content and Projects

The source also provides a lengthy list of other simulations, apps, and projects, mostly focused on physics and mathematics. This list shows the breadth of resources produced by the Open Educational Resources / Open Source Physics @ Singapore project. This indicates a commitment to developing a comprehensive suite of educational tools. A selection of those include:

• Symmetry Block JavaScript HTML5 Applet Simulation Model
• Work Done on a Block (Work-Energy Principle) JavaScript HTML5 Applet Simulation Model
• Projectile Motion with System of Masses and Spring JavaScript HTML5 Applet Simulation Model
• Simple Electric Circuit JavaScript Simulation Applet HTML5

7. Conclusion

This vector component simulation provides a useful and engaging tool for students learning about vectors in physics. Its interactive features, combined with clear mathematical explanations and formulas, make it a valuable resource for reinforcing the core concepts of vector resolution and calculations. The surrounding resources and projects demonstrate a broader commitment to open education and interactive learning within the Singapore educational system.

Vector Components Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

1. What is a vector quantity and how does it differ from a scalar quantity?
2. List three examples of vector quantities and three examples of scalar quantities.
3. Why is it useful to decompose a vector into its components?
4. If a vector points directly to the right, what are the values of its vertical (Ay) and horizontal (Ax) components?
5. What are the formulas used to calculate the x-component (Ax) and y-component (Ay) of a vector, given its magnitude (|A|) and angle (θ)?
6. How do you find the magnitude of a vector if you know its x and y components?
7. Explain the relationship between the angle of a vector and the inverse tangent (tan⁻¹) function.
8. In the provided simulation, what happens when you click the PLAY button after selecting only the Ax checkbox?
9. According to the simulation, what is a common unit used to express the angle of a vector?
10. What are two examples given of quantities that have both magnitude and direction but are NOT vectors?

Answer Key

1. A vector quantity has both magnitude and direction, while a scalar quantity has only magnitude. Vectors require specific rules for addition, whereas scalar quantities do not.
2. Vector examples: displacement, velocity, force. Scalar examples: speed, time, mass.
3. Decomposing a vector into its components simplifies complex calculations by allowing us to work with orthogonal (perpendicular) axes. This helps in analyzing how the vector affects motion in horizontal and vertical directions independently.
4. If a vector points directly to the right, the vertical component (Ay) is zero, and the horizontal component (Ax) is equal to the magnitude of the vector.
5. The x-component (Ax) is calculated as Ax = |A|cos(θ), and the y-component (Ay) is calculated as Ay = |A|sin(θ), where |A| is the magnitude of the vector and θ is the angle relative to the x-axis.
6. The magnitude of a vector can be calculated using the Pythagorean theorem: |A| = √ (Ax² + Ay²). This uses the components to find the hypotenuse, which is the vector's length.
7. The inverse tangent (tan⁻¹) is used to calculate the angle of a vector. If you know the x and y components of the vector, you can use tan⁻¹(Ay/Ax) to find the angle.
8. When the Ax checkbox is selected and PLAY is clicked, the simulation will animate the effects of changing the x-component while leaving the y-component constant, resulting in a vector that changes magnitude and angle along the horizontal axis.
9. According to the simulation, angles of vectors are commonly expressed in degrees.
10. The two examples given of quantities with both magnitude and direction that are NOT vectors are angular displacement and electric current.

Essay Questions

Instructions: Answer each of the following in essay format.

1. Discuss the importance of understanding vector components in physics. Provide real-world examples of how the concept of vector decomposition is used in various fields.
2. Explain the process of resolving a vector into its components and then, given its components, reconstituting it. Describe the mathematical relationships that govern this process.
3. Analyze the interactive simulation, focusing on how it helps students understand vector components. Explain the different functionalities of the simulation and how they facilitate learning.
4. Compare and contrast scalar and vector quantities. Describe the specific properties of vectors that distinguish them from scalar quantities.
5. Discuss the application of vector concepts in at least two different physical phenomena, such as projectile motion and forces in mechanical systems.

Glossary of Key Terms

Vector: A quantity that has both magnitude (size) and direction. It is often represented by an arrow, where the length of the arrow indicates magnitude and the direction of the arrow indicates the direction of the vector. Scalar: A quantity that has only magnitude and no direction. Examples include time, mass, and temperature. Magnitude: The length or size of a vector, representing its quantity. It is always a non-negative value. Component of a Vector: The projection of a vector onto a specific axis, usually either the x-axis (horizontal component) or the y-axis (vertical component) in a two-dimensional system. Vector Decomposition (Resolution): The process of breaking a vector down into its components. This is often done to make calculations easier or to analyze the vector's influence in different directions. x-component (Ax): The horizontal component of a vector, usually found using the formula Ax = |A|cos(θ). y-component (Ay): The vertical component of a vector, usually found using the formula Ay = |A|sin(θ). Angle (θ): The angle a vector makes with a reference axis, typically the positive x-axis, used in trigonometric calculations to find components. Inverse Tangent (tan⁻¹): A trigonometric function used to find the angle of a vector given its components; θ = tan⁻¹(Ay/Ax). Resultant Vector: A single vector that is equivalent to the combined effect of two or more vectors. Its components are determined by adding the individual vector components.

Topics

Measurement of length and time

Description

A vector is a quantity that has both magnitude and direction. Displacement, velocity, acceleration, and force are the vector quantities. in simpler examples, vectors were simply directed up, down, left or right. In situations in which vectors are directed at angles to the customary x(horizontal)-y(vertical) coordinate axes, a useful mathematical trick will be employed to transform the vector into two parts with each part being directed along the coordinate axes. For example, a vector that is directed northwest can be thought of as having two parts - a northward part and a westward part. A vector that is directed upward and rightward can be thought of as having two parts - an upward part and a rightward part.

Engage:

Vectors are fundamental in the physical sciences. They can be used to represent any quantity that has magnitude, has direction, and which adheres to the rules of vector addition. An example is velocity, the magnitude of which is speed. For example, the velocity 4 meters per second upward could be represented by the vector $A_{y}$ = (0,4) (in 2 dimensions with the positive y axis as 'up'). Another quantity represented by a vector is force, since it has a magnitude and direction and follows the rules of vector addition. Vectors also describe many other physical quantities, such as linear displacement, displacement, linear acceleration, angular acceleration, linear momentum, and angular momentum. Other physical vectors, such as the electric and magnetic field, are represented as a system of vectors at each point of a physical space; that is, a vector field. Examples of quantities that have magnitude and direction but fail to follow the rules of vector addition: Angular displacement and electric current. Consequently, these are not vectors.

Component:

As explained above a vector is often described by a set of vector components that add up to form the given vector. Typically, these components are the projections of the vector on a set of mutually perpendicular reference axes (basis vectors). The vector is said to be decomposed or resolved with respect to that set. For simplicity, let's assume x and y direction as the reference axes, referring to the model above.

the equations for the components are:

 $A_{x} = A cos( \theta)$

 $A_{y} = A sin( \theta)$

 

Model:

This model uses the following equations:

Length or Magnitude |A|:

The length or magnitude or norm of the vector a is denoted by |A|.

 $|A| = \sqrt {( A_{x}^{2}+A_{y}^{2})}$

Angle:

The angle in radian of the vector that makes with the positive x axis is

$\theta = tan^{-1} (\frac {A_{y}}{A_{x}})$

the conversion to degree is

$\theta_{degree} = (tan^{-1} (\frac{A_{y}}{A_{x}}) )( \frac{180}{\pi})$

or

$\theta_{degree} = ( \theta )( \frac{180}{\pi})$

in the design of the slider values which shows in degree, the equation that converts back from degree to radian is used

$\theta = ( \theta_{degree} )( \frac{\pi}{180})$

Calculate the components of the vector A

1. click reset to generate a new random vector A of length |A| at an angle of theta to the positive x axis.
2. use the formula Ax = |A|cos(theta) to find the x direction component Ax.
3. use the formula Ay = |A|sin(theta) to find the y direction component Ay.
4. click reset to random generate a new vector A.
5. test yourself whether you have enough practice calculating Ax and Ay.

Other interesting fun activities

1. this model can be used to calculate any length |A| by keying in the values such as |A| =500 and theta = 63 degrees. Select the checkboxes Ax and Ay to see the new answers. 
2. when Ax is selected, the PLAY button animates the effects of changing Ax alone.
3. when Ay is selected, the PLAY button animates the effects of changing Ay alone.
4. explore your own vector(s) here to test your understanding.
5. leave me a Google+ comment/question/requests etc herehttp://weelookang.blogspot.sg/2014/10/components-vector-model.html 

Sample Learning Goals

(e) state what is meant by scalar and vector(how to resolve) quantities and give common examples of each

 

Version:

1. http://weelookang.blogspot.sg/2014/10/components-vector-model.html

2. http://weelookang.blogspot.sg/2014/10/components-vector-model.html CLICK https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_horizontalvertical/horizontalvertical_Simulation.xhtml author: lookang, Fu-Kwun, Andreu Glasmann, Wolfgang Christian, and Mario Belloni offline use: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_horizontalvertical.zip source: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_src_horizontalvertical.zip author of EJS 5: Paco.

3. http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=662.0 Represent a vector as horizontal and vertical components applet by Loo Kang Wee and Fu-Kwun Hwang
4. http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=661.0 Magnitude of a Vector by Loo Kang Wee and Fu-Kwun Hwang

 

Other Resources

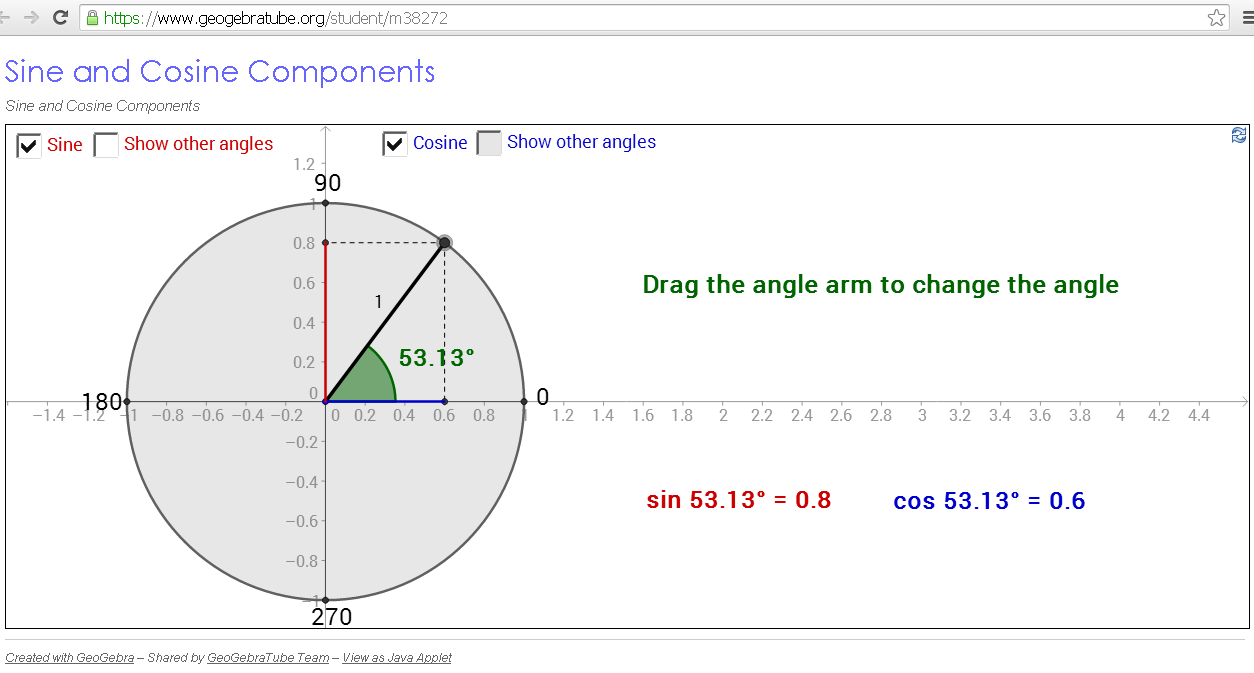
1. Example JavaScript Model Ill 3.1: Vector Decomposition written by Andreu Glasmann, Wolfgang Christian, and Mario Belloni 
2. https://www.geogebratube.org/student/m38272 

FAQ: Vectors and Vector Components

1. What is a vector, and how does it differ from a scalar? A vector is a quantity that has both magnitude (size) and direction. Examples of vector quantities include displacement, velocity, acceleration, and force. A scalar, on the other hand, is a quantity that only has magnitude. Examples of scalar quantities include temperature, speed (the magnitude of velocity), and mass. The key difference is that vectors have an associated direction, while scalars do not. Vectors also adhere to specific rules of vector addition which certain quantities that possess magnitude and direction do not, disqualifying them as vectors (e.g. angular displacement).
2. Why are vectors important in physics? Vectors are fundamental in physics because they allow us to accurately represent and manipulate physical quantities that have both magnitude and direction. Many laws of physics involve relationships between vector quantities, and they provide a framework for analysis and problem-solving in various areas of mechanics, electromagnetism, and more. They can represent diverse physical aspects including linear displacement, acceleration, momentum, and even abstract concepts such as electric and magnetic fields (expressed as vector fields).
3. What are vector components and how are they used? Vector components are the projections of a vector onto a set of mutually perpendicular reference axes. Typically, these are the x (horizontal) and y (vertical) axes. Breaking down a vector into its components allows us to analyze its effect in different directions independently. A vector can be considered as the sum of its components (A = Ax + Ay). The components are found using trigonometry with the magnitude of the vector and the angle it makes with the x-axis.
4. How do you calculate the x and y components of a vector? Given a vector A with magnitude |A| and an angle θ relative to the positive x-axis, the components are calculated as follows:

• The x-component, Ax, is given by: Ax = |A| cos(θ)
• The y-component, Ay, is given by: Ay = |A| sin(θ) These formulas essentially use basic trigonometry to project the vector onto the x and y axes.

1. How is the magnitude or length of a vector calculated from its components? The magnitude or length (|A|) of a vector can be calculated from its x-component (Ax) and y-component (Ay) using the Pythagorean theorem. The formula is: |A| = √( Ax2 + Ay2) This formula works by forming a right triangle from the x and y components, with the magnitude being the hypotenuse.
2. How is the angle of a vector determined from its components? The angle (θ) a vector makes with the positive x-axis can be determined using the inverse tangent (arctan or tan-1) function of the ratio of the y-component (Ay) to the x-component (Ax) as follows: θ = tan-1(Ay/ Ax) This angle is often measured in radians and can be converted to degrees using the conversion factor of 180/π.
3. How do the interactive simulations help in understanding vectors? The interactive simulations allow users to visualize vectors and their components. You can manipulate vector properties (magnitude and angle) and observe how the x and y components change in response. The simulations often include features like animations that demonstrate the effects of each component separately and test quizzes that give users practice calculating the components, allowing for a hands-on understanding of vector concepts. By allowing users to directly manipulate parameters and see instant results, the simulations reinforce the relationships between the vector, its components, its magnitude, and its angle.
4. What are some examples of physical quantities that can be represented by vectors? Many physical quantities can be described with vectors:

• Displacement: Change in position with a specific direction.
• Velocity: Rate of change of displacement with a specific direction.
• Acceleration: Rate of change of velocity with a specific direction.
• Force: A push or pull with a specific direction.
• Momentum: A measure of mass in motion with a specific direction
• Electric and magnetic fields (as a system of vectors at each point in space) These quantities all require both magnitude and direction to be completely defined.