v11 with restrictions to form a outline only, 2 triangle is ok, and validateAndStart(), must start and end at the centre line
Credits
['Kang Rui', 'meiYoke', 'looKang']
v10 with restrictions to form a outline only, 2 triangle is ok, and validateAndStart()
Credits
['Kang Rui', 'meiYoke', 'looKang']
v9 with restrictions to form a outline only
Credits
['Kang Rui', 'meiYoke', 'looKang']
Credits
['Kang Rui', 'meiYoke', 'looKang']
Credits
['']
 |
| 🔗 Launch the Interactive Simulation |
Exploring Line Symmetry with WebEJS: A Hands-On Interactive
Introduction
Symmetry is a fundamental concept in mathematics, and this Line Symmetry Interactive is designed to help students visualize and explore the idea of reflectional symmetry dynamically. Built using WebEJS (Easy JavaScript Simulations), this tool enables users to create patterns and observe their symmetrical counterparts based on a selected axis.
Features of the Interactive
- Click to Draw: Users can click on grid points to create lines and design a pattern.
- Reflectional Symmetry: The simulation allows symmetry to be generated across vertical, horizontal, and diagonal axes.
- Customizable Settings: Users can select:
- The type of symmetry (vertical, horizontal, diagonal).
- The reflection axis position (left, right, center).
- Instant Symmetry Visualization: Pressing the "Start" button generates the symmetric counterpart of the drawn pattern.
- Interactive Learning: Buttons for checking answers, clearing scenarios, and resetting responses make it useful for self-guided learning.
How It Works
- Choose the symmetry type using the dropdown menu (e.g., vertical, left).
- Draw a shape by clicking on grid points to connect lines.
- Press "Start" to generate the mirrored counterpart.
- Use "Check" to verify correctness.
- Clear and try again with different scenarios.
Why Use WebEJS?
WebEJS is an ideal platform for building educational simulations due to its:
- Ease of Use: Educators can modify and adapt the interactive without deep programming knowledge.
- Browser-Based Execution: No installation required—students can access it directly via a URL.
- Customizability: The WebEJS editor allows modifications in real time, making it flexible for various learning needs.
Applications in the Classroom
- Primary and Secondary Math Lessons: Introduce symmetry concepts interactively.
- STEM Activities: Encourage students to explore geometric transformations.
- Gamification of Learning: Students can challenge themselves to create complex shapes and predict their symmetrical counterparts.
Try It Yourself!
🔗 Launch the Interactive Simulation
Sample Learning Goals
[text]
For Teachers
[text]
Research
# Centreline‑Aware Symmetry Outline Validator (WebEJS + xAPI)
This post documents the prompt‑driven journey and implementation details to build a robust, “centreline‑aware, closed‑figure” validation workflow for a WebEJS simulation that teaches line symmetry.
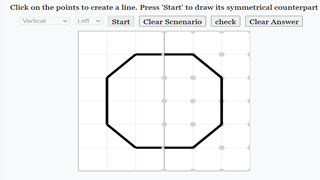
Students draw on one side of a separation line (centreline), then mirror their construction. The system:
- Prevents illegal connections during drawing (no overlaps, no self‑intersections, no branching, no duplicates).
- Accepts only closed figures for mirroring (including shapes that are “closed” by the centreline as a boundary).
- Supports multiple boundary‑closed shapes (e.g., two triangles sharing the centreline).
- On Start, simplifies the drawing to keep only the accepted closed shapes and warns the learner if anything was removed.
All core logic lives in `_source.ejss`.
## TL;DR
- While drawing: enforce “outline‑only” constraints.
- On Start (validate): prune to closed figures (centreline counts as boundary) and ignore extraneous segments.
- Optionally accept multiple shapes touching the centreline via consecutive contact linking.
- Alert the student if simplification removed extra segments.
## How to run
- Local preview: open `index.html` in a browser.
- WebEJS:
1) Zip the entire folder (including `_source.ejss`, `_simulation.xhtml`, `index.html`, and `_ejs_library`).
2) Upload the zip to WebEJS. It will detect `_source.ejss` and run the model.
Drawing flow:
1) Choose the line type (Vertical / Horizontal / Diagonal (+) / Diagonal (−)) and side.
2) Click two lattice points to draw segments. Illegal moves show a pop‑up reason and are blocked.
3) Press Start to validate; only closed shapes (centreline counts) remain and will be mirrored.
4) If extra lines existed, an alert tells the student how many were removed (“simplified”).
---
## Prompt strategy: From idea → constraints → validation
Use these prompt patterns to replicate the build in another project.
1) Explain the current implementation
- Prompt: “Read `_source.ejss` and explain how lines on the left panel are formed.”
- Outcome: Mapped how `ShapeSet2D` and `SegmentSet2D` bind to arrays, and how click handlers append segments with `undefined` separators.
2) Enforce outline‑only during drawing
- Prompt: “Add a validator that blocks branching, duplicate/overlapping edges, self‑intersections, and drawing after closure.”
- Change:
- Add `outlineRules` page with `canAddOutlineEdge()` plus geometry helpers.
- Call `canAddOutlineEdge()` in `onClickPlottedPoints()` and `onClickMirroredPoints()` before adding segments.
3) Pop‑up for illegal moves
- Prompt: “Show `alert()` with a reason when a connection is rejected.”
- Change: Enable `alert(check.reason)` in both click handlers.
4) Prune non‑closed segments
- Prompt: “Automatically remove tails/branches not part of a closed figure.”
- Change:
- `pruneToClosedFiguresIfAny()` finds cycles, updates `points[].connected`, and rebuilds arrays.
- Tuned so drawing remains visible; pruning happens when appropriate.
5) Validate on Start
- Prompt: “Validate only when Start is pressed; block if not closed.”
- Change:
- New `startValidation` page with `validateAndStart()`.
- Start button calls `validateAndStart()`; drawing‑time pruning removed.
- If not closed, alert and stay on the left.
6) Centreline‑as‑boundary closedness
- Prompt: “A figure that touches the centreline should count as closed using that line as a boundary.”
- Change:
- `_isOnSeparationLine(p)`: detect contact with active centreline (Vertical/Horizontal/Diag±).
- `_augmentAdjacencyWithSeparationLine(points)`: add virtual edges along the centreline between contacts.
- `_cycleKeysWithBoundary()` + `pruneToClosedFiguresWithBoundary(...)`: accept cycles that leverage the centreline for closure.
7) Accept multiple shapes that share the centreline
- Prompt: “Support multiple boundary‑closed shapes (e.g., two triangles).”
- Change:
- Link **every consecutive** centreline contact (0–1, 1–2, 2–3, …), not only disjoint pairs (0–1, 2–3).
8) Warn on simplification at Start
- Prompt: “On Start, alert if extra lines were removed.”
- Change:
- In `validateAndStart()`, compare counts from `_extractSegments()` before vs after pruning and alert if reduced.
---
## Key functions and where they live
- Page: `outlineRules`
- `canAddOutlineEdge(points, idxA, idxB)`: outline‑only guard (no branches/intersections/overlap/duplicates; degree ≤ 2).
- `_extractSegments(points)`: unique undirected segments from `points[].connected`.
- `pruneToClosedFiguresIfAny(points, lineX, lineY, sizeX, sizeY)`: true cycles (no boundary).
- `pruneToClosedFiguresWithBoundary(points, lineX, lineY, sizeX, sizeY)`: cycles when the centreline is a boundary.
- `_isOnSeparationLine(p)`: centreline contact detection for all four line types.
- `_augmentAdjacencyWithSeparationLine(points)`: adds **virtual edges between every consecutive centreline contact**.
- `_cycleKeysWithBoundary(points)`: leaf‑strips augmented graph to find cycle vertices.
- `_rebuildSegmentArraysFromSegs(segs, lineX, lineY, sizeX, sizeY)`: rewrites the bound arrays in place.
- Page: `startValidation`
- `validateAndStart()`: Start button entry point; prunes with boundary awareness, clears ghost buffers, warns if simplified, then calls `initMirroredPoints()`.
- Pages: `onClickPlottedPoints`, `onClickMirroredPoints`
- Call `canAddOutlineEdge()` before appending a segment to all bound arrays.
---
## Code snippets (ready to paste)
### 1) Start button wiring (HTML view)
```xml
<Property name="OnPress"><![CDATA[validateAndStart();]]></Property>
```
### 2) Alert when simplification removed segments (in startValidation.validateAndStart)
```js
function validateAndStart() {
// Count segments BEFORE pruning
const prevSegs = _extractSegments(plottedPoints).length;
// Prune considering the centerline as a virtual boundary
var accepted = pruneToClosedFiguresWithBoundary(
plottedPoints, plottedLineX, plottedLineY, plottedSizeX, plottedSizeY
);
// Clear ghost visuals to avoid confusion
if (typeof ghostLineX !== "undefined") {
ghostLineX = [undefined];
ghostLineY = [undefined];
ghostSizeX = [undefined];
ghostSizeY = [undefined];
}
// If nothing acceptable yet, stop here
if (!accepted) {
alert("Please create a closed figure on the left (the centre line counts as a boundary). Open lines were ignored and will not be mirrored.");
return;
}
// Count segments AFTER pruning
const postSegs = _extractSegments(plottedPoints).length;
// Notify if simplification removed any segments
if (postSegs < prevSegs) {
const removed = prevSegs - postSegs;
alert(`Your figure was simplified to a closed shape. Removed ${removed} extraneous segment(s).`);
}
// Proceed to mirrored side
initMirroredPoints();
}
```
### 3) Centreline augmentation: link every consecutive contact
```js
// After collecting and sorting boundary contacts along the active centreline:
for (var t = 0; t + 1 < boundary.length; t++) {
var k1 = boundary[t].k, k2 = boundary[t+1].k;
ensure(k1); ensure(k2);
adj.get(k1).push(k2);
adj.get(k2).push(k1);
deg.set(k1, deg.get(k1) + 1);
deg.set(k2, deg.get(k2) + 1);
}
```
---
## Testing checklist
- While drawing
- Illegal connections show a reason via `alert()`.
- Edges render as drawn; no pruning yet.
- On Start
- If not closed (even with centreline), alert and stay on the left.
- If boundary‑closed, only accepted shapes remain (extraneous segments removed).
- If simplification occurred, a pop‑up tells how many segments were removed.
- Proceed to right side to mirror exactly the accepted shapes.
- Special scenarios
- “Two triangles” touching the centreline (zig‑zag with 3 contacts): accepted and pruned correctly.
- Horizontal / Diagonal (+/−) centrelines: contact detection via
- Vertical: `p.x === graphX/2`
- Horizontal: `p.y === graphY/2`
- Diagonal (+): `(x − y) === (midX − midY)`
- Diagonal (−): `(x + y) === (midX + midY)`
## Troubleshooting
- The first edge disappears when I draw:
- Ensure that pruning is only invoked in `validateAndStart()` (Start phase), not during click.
- A centreline‑touching polygon is rejected:
- Verify `_isOnSeparationLine(p)` for your line type.
- Ensure coordinates are integer grid points; midpoints computed as `graphX/2`, `graphY/2`.
- Two‑triangle case still not accepted:
- Confirm augmentation links **every consecutive** contact (not just 0–1, 2–3).
---
## Attribution
- Built on WebEJS (EJS 6.x compatible) using `ShapeSet2D` and `SegmentSet2D`.
- Geometry validation and pruning authored via iterative, prompt‑driven development.
Video
[text]
Version:
Other Resources
[text]
end faq
{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}
- Details
- Written by Loo Kang Wee
- Parent Category: Interactive Resources
- Category: Mathematics
- Hits: 791