toFixed(0)
Credits
['kangRui', 'meiYoke', 'looKang']
Credits
['kangRui', 'meiYoke', 'looKang']
Credits
['']
https://youtu.be/iE848le6Wn4?si=vTUJyrkOVgA9ZQT1
 |
| iwant2study.org |
Thinking Aloud: Fill the Tank – Interactive Math Puzzle
Introduction
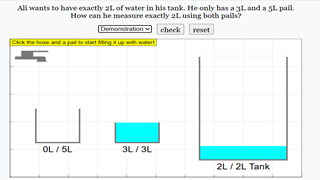
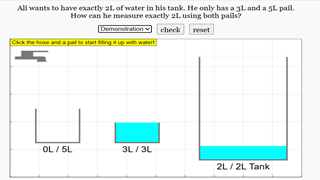
The Thinking Aloud: Fill the Tank interactive simulation challenges users to solve a classic water-pouring problem using logical reasoning and experimentation. In this scenario, Jia Hao needs to measure exactly 4L of water using only a 5L pail and a 3L pail. The user must figure out the correct sequence of actions to achieve the goal.
This simulation, available at Thinking Aloud: Fill the Tank, encourages users to develop problem-solving skills and understand the principles behind measuring volume with limited tools.
How to Play
- Click the tap to fill one of the pails with water.
- Click a pail to pour water into another pail or into the target tank.
- Continue the process until exactly 4L of water is collected in the tank.
- Click Check to verify your solution.
- Click Reset to start over.
The interface includes:
- A 5L pail and a 3L pail.
- A 4L target tank.
- A Scenario selector for different challenges.
- Buttons for checking the solution and resetting the simulation.
The Mathematical Thinking Behind It
This problem is a classic example of using the greatest common divisor (GCD) to measure specific volumes. The 5L and 3L pails can only measure amounts that are multiples of GCD(5,3) = 1L, meaning they can measure any quantity that is a sum or difference of these values.
Solution to Fill 4L:
- Fill the 3L pail completely from the tap.
- Pour the 3L into the 5L pail.
- Refill the 3L pail from the tap.
- Pour 2L from the 3L pail into the 5L pail (which now holds 5L and is full).
- The remaining 1L in the 3L pail is the key.
- Empty the 5L pail completely.
- Transfer the 1L from the 3L pail to the 5L pail.
- Refill the 3L pail again and pour it into the 5L pail.
- Now, the 5L pail contains exactly 4L, which can be poured into the target tank.
This problem demonstrates modular arithmetic and logical deduction, making it a great exercise in computational thinking.
Learning Outcomes
- Develop problem-solving skills by experimenting with different sequences.
- Apply number theory concepts like GCD and modular arithmetic in a real-world scenario.
- Encourage logical reasoning through trial and error.
- Enhance mathematical intuition with hands-on exploration.
This interactive aligns well with the heuristics approach in problem-solving often emphasized in mathematics education.
Conclusion
The Thinking Aloud: Fill the Tank simulation is an engaging way to explore problem-solving with water measurement. It serves as an excellent classroom tool for students to practice logical reasoning, sequencing, and number properties. Try it out at iwant2study.org and challenge yourself to find the most efficient way to fill the tank!
Sample Learning Goals
[text]
Interactive Inspiration
| Textbook 2A Chapter 3 Length p. 84 | Interactive Designed |
|
|
|
Read Less
Interactive Overview
The "Find the Shortest Path" interactive is a thoughtfully designed activity that encourages students to engage in logical reasoning, route optimization, and spatial visualization. The task requires students to help a character, Susan, find the shortest route that allows her to visit specified locations.
At its core, this interactive helps develop students’ decision-making skills under constraints. By evaluating and comparing the total distance of different possible routes, students learn to consider multiple variables at once — order of visit, direction, and connection availability. The process mirrors real-life problem-solving situations where careful step-by-step planning is required, such as organizing a set of instructions to complete a task efficiently or planning the sequence of actions in a project. It trains learners to think ahead, anticipate outcomes, and refine their strategies based on logical sequencing.
Read Less
Feedback From Students
| Question | |||
| Q1: Is the instruction on how to play the Mini-Game clear? | Not Clear: 2 | Somewhat Clear: 16 | Very Clear: 9 |
| Q2: Are the tasks easy to understand? | Not Easy: 2 | Understand Some: 15 | Totally Understand: 10 |
| Q3: Which part of the Mini-Game can be improved or made better? |
Theme: Students want clearer, more straightforward questions with fewer options and better guidance. |
||
| Q4: I enjoyed playing the Mini-Game. | Do Not Enjoy: 2 | Somewhat Enjoy: 12 | Enjoy Very Much: 13 |
| Q5: Which part of the Mini-Game did you enjoy? |
Theme: Students enjoyed the problem-solving and the fun of playing, especially when they succeeded. |
||
| Q6: Which task is the easiest to you? | Task A: 18 Task B: 4 Task C: 1 Task D: 4 |
||
| Q7: Which task is the most difficult to you? | Task A: 2 Task B: 2 Task C: 6 Task D: 17 |
||
| Q8: Why is the task difficult? |
Theme: The main difficulties came from overwhelming options and unclear wording in the tasks. |
||
Read Less
ITT Analysis
Teachers may also leverage the ITT Analysis tool in SLS, which provides AI-generated overviews to support a deeper understanding of students’ thinking processes

Read Less
Interactive Activity Data
After completing the interactive activity, students can click the Submit button to view a summary of their activity data.
Example:
Example of a student's activity data:

Using data from the activity, teachers can export the provided data and utilize AI tools, such as ChatGPT/PairChat, to perform further analysis. The following examples illustrate two types of analysis that can be conducted: CAIT and Metacognition.
e21CC - CAIT Analysis
Example:
Critical Thinking Assessment
CAIT 1: Exercises sound reasoning and decision-making
Student demonstrates developing critical thinking skills through his systematic approach to route planning. His ability to persist through 7 attempts in Task A shows reasoning processes, though the multiple incorrect calculations suggest his decision-making could be strengthened. The improvement to only 3 attempts in Task B indicates he can learn from experience and apply better reasoning.
CAIT 2: Uses metacognition to enhance, monitor and regulate thinking
Strong evidence of metacognitive awareness is shown through student's ability to modify his approach between attempts. The dramatic improvement from Task A (7 attempts, 3m 37s) to Task B (3 attempts, 52s) demonstrates he reflected on his learning experience and made effective modifications to his problem-solving strategy.
Adaptive Thinking Assessment
CAIT 3: Assesses different contexts and situations to make connections and draw new insights
Student shows emerging adaptive thinking by recognising that Task B, whilst similar to Task A, required different route combinations. His varied approaches across attempts (changing starting points, route sequences) indicate awareness that different contexts may require different strategies.
CAIT 4: Manages complexities and ambiguities by adjusting perspective and strategies
Evidence of adaptive strategy adjustment is clear in his progression from complex multi-location routes (Attempt 1: 5 locations) to more efficient 3-location solutions (Attempt 7). His willingness to try completely different route sequences shows flexibility in managing the complexity of the navigation problem.
Inventive Thinking Assessment
CAIT 5: Explores possibilities and generates novel and useful ideas
Student demonstrates inventive thinking through his exploration of multiple route possibilities. He generates various combinations of locations and sequences, showing creativity in problem-solving approaches. His routes show both replication of patterns (similar sequences) and modification of existing ideas (changing starting points and sequences).
CAIT 6: Evaluates and refines ideas to formulate novel and useful solutions
His progression shows evaluation and refinement skills. The successful completion of both tasks indicates he can assess which approaches work and refine his strategies accordingly. The significant time reduction between tasks suggests effective evaluation of his problem-solving methods.
Overall CAIT Assessment
Student demonstrates solid foundational skills across all three thinking domains, with particular strength in metacognitive awareness and adaptive strategy adjustment. His persistent approach and clear learning progression indicate good potential for further 21st century competency development in mathematical problem-solving contexts.
Metacognition Analysis
Example:
Metacognition - 3 components
Metacognitive Knowledge
Student demonstrates varying levels of metacognitive knowledge across the different types:
Declarative Knowledge (Knowing What): Student appears to understand the basic task requirements - he knows he needs to visit specific locations and calculate distances. However, his knowledge of the optimal routes and distance calculations seems incomplete initially, as evidenced by the multiple incorrect attempts.
Procedural Knowledge (Knowing How): Student shows developing procedural knowledge. In Task A, he experiments with different route sequences, indicating he understands the process of route planning. His improvement from Task A (7 attempts) to Task B (3 attempts) suggests he's acquiring better procedural strategies for approaching similar problems.
Conditional Knowledge (Knowing When and Why): This appears to be Student weakest area initially. In Task A, he makes several attempts with similar route patterns (attempts 2, 4, and 6 all resulted in 110m), suggesting limited awareness of when to change his strategic approach fundamentally rather than making minor adjustments.
Metacognitive Monitoring
Student demonstrates active monitoring throughout his problem-solving process:
- He consistently tracks his distance calculations and recognises when they're incorrect
- His attempt logs show he's aware of his progress and time spent
- The pattern of attempts suggests he's monitoring his strategies and making adjustments
- However, his monitoring in Task A shows some inefficiency - he repeated similar unsuccessful approaches multiple times before significantly changing his strategy
Metacognitive Regulation
Student's regulatory decisions show both strengths and areas for improvement:
Effective Regulation:
- He persists through multiple attempts rather than giving up
- Shows significant improvement between tasks (Task A: 7 attempts, 3m 37s vs Task B: 3 attempts, 0m 52s)
- Successfully modifies his approach when previous attempts fail
- Makes the decision to continue or change strategies based on feedback
Areas for Improvement:
- In Task A, regulation appears somewhat inefficient - he makes similar attempts (2, 4, 6) before making more substantial strategic changes
- Could benefit from earlier recognition of when a fundamental strategy change is needed rather than minor route adjustments
Overall Metacognitive Development
Student shows clear metacognitive growth between Task A and Task B. His dramatic improvement in efficiency suggests he's learning to better regulate his problem-solving approach and apply knowledge gained from previous attempts. The fact that he didn't attempt Tasks C and D might indicate improved self-awareness about task difficulty or time management, though this would require further investigation to confirm.
His metacognitive profile suggests a learner who benefits from experience and feedback, with particular strength in persistence and monitoring, but with room for improvement in strategic flexibility and early recognition of when fundamental approach changes are needed.
[text]
Research
[text]
Video
[text]
Version:
- http://weelookang.blogspot.sg/2016/02/vector-addition-b-c-model-with.html improved version with joseph chua's inputs
- http://weelookang.blogspot.sg/2014/10/vector-addition-model.html original simulation by lookang
Other Resources
[text]
MModule
HELP
MOE Library
P2 Thinking Aloud Task: Length (Find the Shortest Path) - Rollout (1.0)
P2 Thinking Aloud Task: Length (Find the Shortest Path) - Rollout (1.0)

Learning Outcome(s)
Subject and Level
|
Mathematics |
Primary 2 |
Content Map and Topic
-
- Acquire mathematical concepts and skills for everyday use and continuous learning in mathematics
- Develop thinking, reasoning, communication, application and metacognitive skills through a mathematical approach to problem-solving
- Build confidence and foster interest in mathematics
- 1.1 measuring
- length in metres
- mass in kilograms/grams
- volume of liquid in litres
- 1.3 comparing and ordering
- lengths
- masses
- volumes
The interactive is a thoughtfully designed activity that encourages students to engage in logical reasoning, route optimization, and spatial visualization. The task requires students to help a character, Susan, find the shortest route that allows her to visit specified locations.
MOE Library
P2 Thinking Aloud Task: Length (Find the Shortest Path) - Rollout (1.0)
1. Slides
MOE Library
P2 Thinking Aloud Task: Length (Find the Shortest Path) - Rollout (1.0)
2. Demonstration
https://youtu.be/iE848le6Wn4?si=vTUJyrkOVgA9ZQT1
MOE Library
P2 Thinking Aloud Task: Length (Find the Shortest Path) - Rollout (1.0)
3. Demonstration (Optional)
Q1:
Demo.zip
Download
FeedbackMarks:/ 1
MOE Library
P2 Thinking Aloud Task: Length (Find the Shortest Path) - Rollout (1.0)
4. Task A
Q1:
Task_A.zip
Download
FeedbackMarks:/ 1
ITT1
Your comment
Did you use any method to find the shortest path quickly?
MOE Library
P2 Thinking Aloud Task: Length (Find the Shortest Path) - Rollout (1.0)
5. Task B
Q1:
Task_B.zip
Download
FeedbackMarks:/ 1
ITT1
Your comment
Did you use any method to find the shortest path quickly?
MOE Library
P2 Thinking Aloud Task: Length (Find the Shortest Path) - Rollout (1.0)
6. Task C
Q1:
Task_C.zip
Download
FeedbackMarks:/ 1
ITT1
Your comment
Did you use any method to find the shortest path quickly?
Q2:
Did you change your method when working on Task C?
Yes
No
ITT2
Your comment
Why did you change your method?
MOE Library
P2 Thinking Aloud Task: Length (Find the Shortest Path) - Rollout (1.0)
7. Task D
Q1:
Task_D.zip
Download
FeedbackMarks:/ 1
ITT1
Your comment
Did you use any method to find the shortest path quickly?
Q2:
Did you change your method when working on Task D?
Yes
No
ITT2
Your comment
Why did you change your method?
MOE Library
P2 Thinking Aloud Task: Length (Find the Shortest Path) - Rollout (1.0)
8. Notes For Teachers (Optional)
Interactive Inspiration
| Textbook 2A Chapter 3 Length p. 84 | Interactive Designed |
|
|
|
Interactive Overview
The "Find the Shortest Path" interactive is a thoughtfully designed activity that encourages students to engage in logical reasoning, route optimization, and spatial visualization. The task requires students to help a character, Susan, find the shortest route that allows her to visit specified locations.
At its core, this interactive helps develop students’ decision-making skills under constraints. By evaluating and comparing the total distance of different possible routes, students learn to consider multiple variables at once — order of visit, direction, and connection availability. The process mirrors real-life problem-solving situations where careful step-by-step planning is required, such as organizing a set of instructions to complete a task efficiently or planning the sequence of actions in a project. It trains learners to think ahead, anticipate outcomes, and refine their strategies based on logical sequencing.
Feedback From Students
| Question | |||
| Q1: Is the instruction on how to play the Mini-Game clear? | Not Clear: 2 | Somewhat Clear: 16 | Very Clear: 9 |
| Q2: Are the tasks easy to understand? | Not Easy: 2 | Understand Some: 15 | Totally Understand: 10 |
| Q3: Which part of the Mini-Game can be improved or made better? |
Theme: Students want clearer, more straightforward questions with fewer options and better guidance. |
||
| Q4: I enjoyed playing the Mini-Game. | Do Not Enjoy: 2 | Somewhat Enjoy: 12 | Enjoy Very Much: 13 |
| Q5: Which part of the Mini-Game did you enjoy? |
Theme: Students enjoyed the problem-solving and the fun of playing, especially when they succeeded. |
||
| Q6: Which task is the easiest to you? | Task A: 18 Task B: 4 Task C: 1 Task D: 4 |
||
| Q7: Which task is the most difficult to you? | Task A: 2 Task B: 2 Task C: 6 Task D: 17 |
||
| Q8: Why is the task difficult? |
Theme: The main difficulties came from overwhelming options and unclear wording in the tasks. |
||
ITT Analysis
Teachers may also leverage the ITT Analysis tool in SLS, which provides AI-generated overviews to support a deeper understanding of students’ thinking processes
Interactive Activity Data
After completing the interactive activity, students can click the Submit button to view a summary of their activity data.
Example:
Example of a student's activity data:
Zoom inZoom outResetDownload
Using data from the activity, teachers can export the provided data and utilize AI tools, such as ChatGPT/PairChat, to perform further analysis. The following examples illustrate two types of analysis that can be conducted: CAIT and Metacognition.
e21CC - CAIT Analysis
Example:
Critical Thinking Assessment
CAIT 1: Exercises sound reasoning and decision-making
Student demonstrates developing critical thinking skills through his systematic approach to route planning. His ability to persist through 7 attempts in Task A shows reasoning processes, though the multiple incorrect calculations suggest his decision-making could be strengthened. The improvement to only 3 attempts in Task B indicates he can learn from experience and apply better reasoning.
CAIT 2: Uses metacognition to enhance, monitor and regulate thinking
Strong evidence of metacognitive awareness is shown through student's ability to modify his approach between attempts. The dramatic improvement from Task A (7 attempts, 3m 37s) to Task B (3 attempts, 52s) demonstrates he reflected on his learning experience and made effective modifications to his problem-solving strategy.
Adaptive Thinking Assessment
CAIT 3: Assesses different contexts and situations to make connections and draw new insights
Student shows emerging adaptive thinking by recognising that Task B, whilst similar to Task A, required different route combinations. His varied approaches across attempts (changing starting points, route sequences) indicate awareness that different contexts may require different strategies.
CAIT 4: Manages complexities and ambiguities by adjusting perspective and strategies
Evidence of adaptive strategy adjustment is clear in his progression from complex multi-location routes (Attempt 1: 5 locations) to more efficient 3-location solutions (Attempt 7). His willingness to try completely different route sequences shows flexibility in managing the complexity of the navigation problem.
Inventive Thinking Assessment
CAIT 5: Explores possibilities and generates novel and useful ideas
Student demonstrates inventive thinking through his exploration of multiple route possibilities. He generates various combinations of locations and sequences, showing creativity in problem-solving approaches. His routes show both replication of patterns (similar sequences) and modification of existing ideas (changing starting points and sequences).
CAIT 6: Evaluates and refines ideas to formulate novel and useful solutions
His progression shows evaluation and refinement skills. The successful completion of both tasks indicates he can assess which approaches work and refine his strategies accordingly. The significant time reduction between tasks suggests effective evaluation of his problem-solving methods.
Overall CAIT Assessment
Student demonstrates solid foundational skills across all three thinking domains, with particular strength in metacognitive awareness and adaptive strategy adjustment. His persistent approach and clear learning progression indicate good potential for further 21st century competency development in mathematical problem-solving contexts.
Metacognition Analysis
Example:
Metacognition - 3 components
Metacognitive Knowledge
Student demonstrates varying levels of metacognitive knowledge across the different types:
Declarative Knowledge (Knowing What): Student appears to understand the basic task requirements - he knows he needs to visit specific locations and calculate distances. However, his knowledge of the optimal routes and distance calculations seems incomplete initially, as evidenced by the multiple incorrect attempts.
Procedural Knowledge (Knowing How): Student shows developing procedural knowledge. In Task A, he experiments with different route sequences, indicating he understands the process of route planning. His improvement from Task A (7 attempts) to Task B (3 attempts) suggests he's acquiring better procedural strategies for approaching similar problems.
Conditional Knowledge (Knowing When and Why): This appears to be Student weakest area initially. In Task A, he makes several attempts with similar route patterns (attempts 2, 4, and 6 all resulted in 110m), suggesting limited awareness of when to change his strategic approach fundamentally rather than making minor adjustments.
Metacognitive Monitoring
Student demonstrates active monitoring throughout his problem-solving process:
- He consistently tracks his distance calculations and recognises when they're incorrect
- His attempt logs show he's aware of his progress and time spent
- The pattern of attempts suggests he's monitoring his strategies and making adjustments
- However, his monitoring in Task A shows some inefficiency - he repeated similar unsuccessful approaches multiple times before significantly changing his strategy
Metacognitive Regulation
Student's regulatory decisions show both strengths and areas for improvement:
Effective Regulation:
- He persists through multiple attempts rather than giving up
- Shows significant improvement between tasks (Task A: 7 attempts, 3m 37s vs Task B: 3 attempts, 0m 52s)
- Successfully modifies his approach when previous attempts fail
- Makes the decision to continue or change strategies based on feedback
Areas for Improvement:
- In Task A, regulation appears somewhat inefficient - he makes similar attempts (2, 4, 6) before making more substantial strategic changes
- Could benefit from earlier recognition of when a fundamental strategy change is needed rather than minor route adjustments
Overall Metacognitive Development
Student shows clear metacognitive growth between Task A and Task B. His dramatic improvement in efficiency suggests he's learning to better regulate his problem-solving approach and apply knowledge gained from previous attempts. The fact that he didn't attempt Tasks C and D might indicate improved self-awareness about task difficulty or time management, though this would require further investigation to confirm.
His metacognitive profile suggests a learner who benefits from experience and feedback, with particular strength in persistence and monitoring, but with room for improvement in strategic flexibility and early recognition of when fundamental approach changes are needed.
- Details
- Written by Loo Kang Wee
- Parent Category: Interactive Resources
- Category: Mathematics
- Hits: 1747