About

1.2.13 Experimental Investigation of Vertical Oscillator              LO (b)

Here is an illustration of how the oscillation of a basic spring-mass system can be investigated using motion sensor.

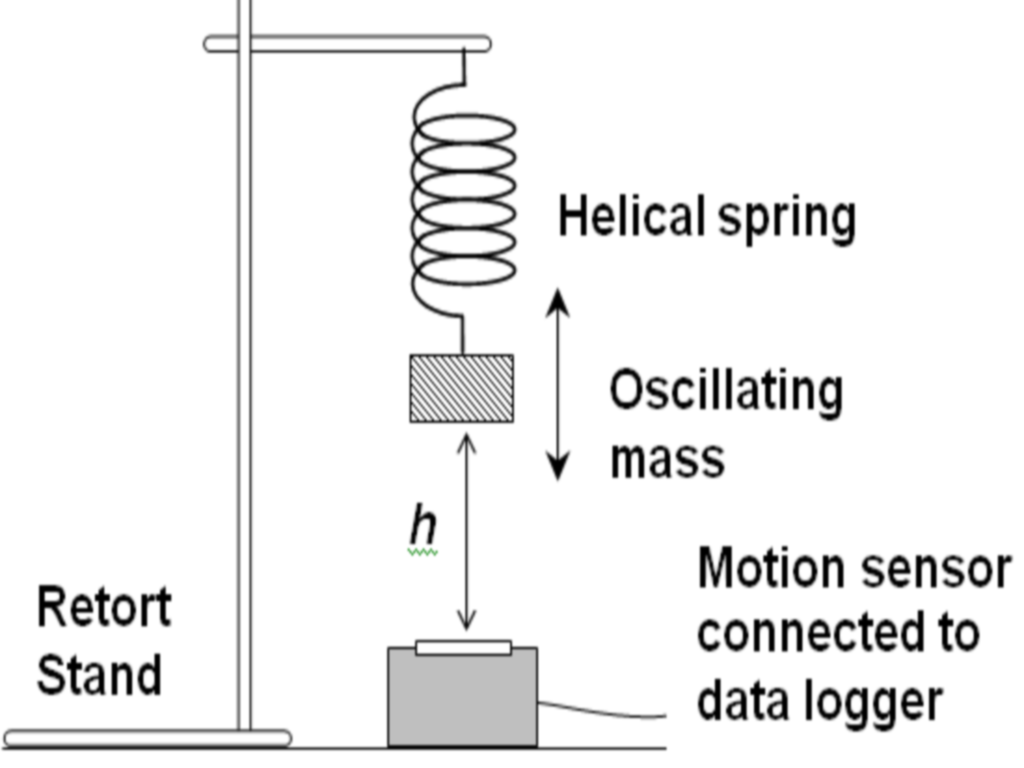
1. Setup the experiment as shown
2. Displace the mass vertically downwards and release it with initial velocity =0 m/s so that it can oscillate freely in an up and down motion.
3. Start the data logger when the oscillations are steady.
4. The motion sensor detects the variation with time of height h.

 Example of data collected is shown


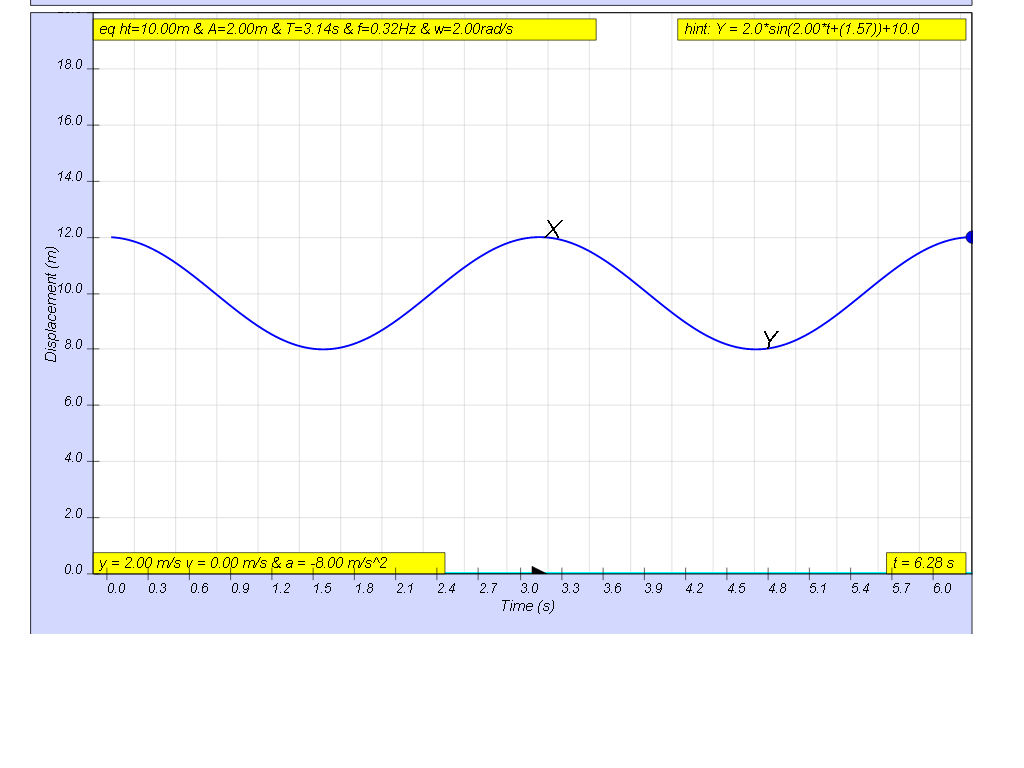
Information of the oscillation can be drawn from Fig. 13.14 as follows:

1. Equilibrium height         h    =  
2. Amplitude            x₀     =            
3. Period                T     =            
4. Frequency            f    =           
5. Angular frequency        ω     =                 
6. Displacement when t = 5.7 s    x    =    

[ 10.0 m , 2.0 m , 3.14 s , 0.32 Hz, 2.00 rad/s, +1.0 m)  

  

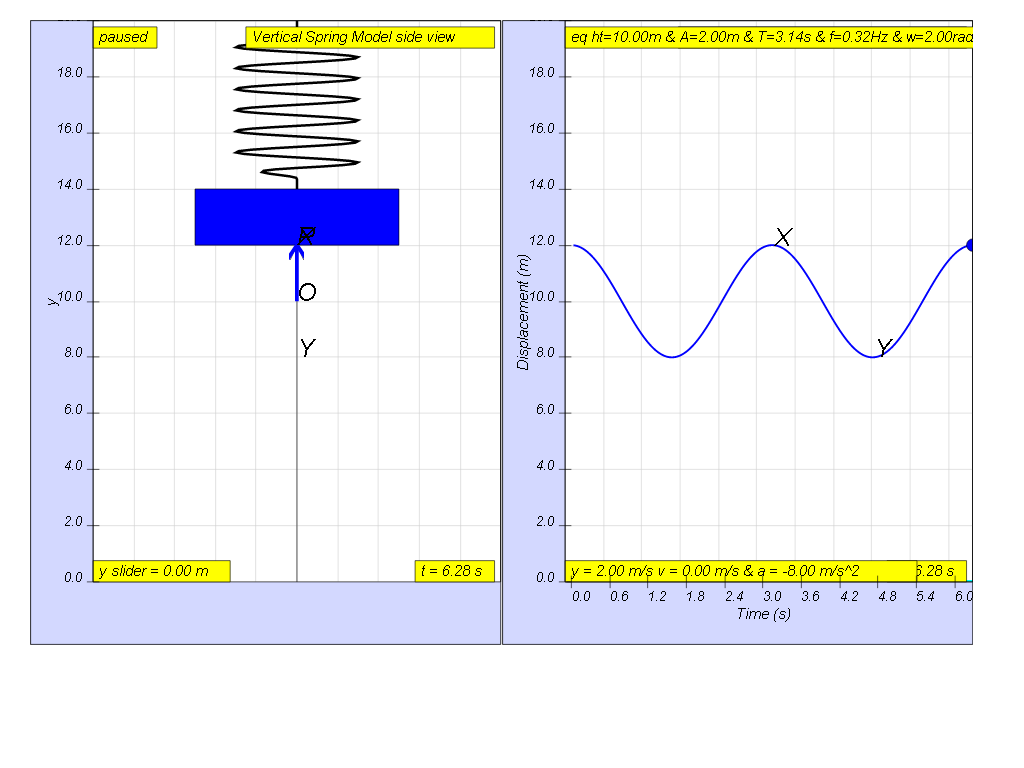
1.2.13.1 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/92

Q1: setup the model to represent the conditions in the example hint: select sensor?,  y = 2.0m, k = 4 N/m   etc.

Q2: setup the model with different conditions of your choice and recalculate the point 1 to 6.

Q3: a student suggests that the conditions of getting the same period of  T = 3.14 s is to ensure the following equation is valid.

$$\sqrt{\frac{m}{k}}=\frac{1}{2}$$collect some data on your own, to verify this claim by this student. Suggest with reasons, whether the claim is supported by the evidences you can collect from the model.

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM163/SHM163_Simulation.xhtml