About

1.2.12 Example 

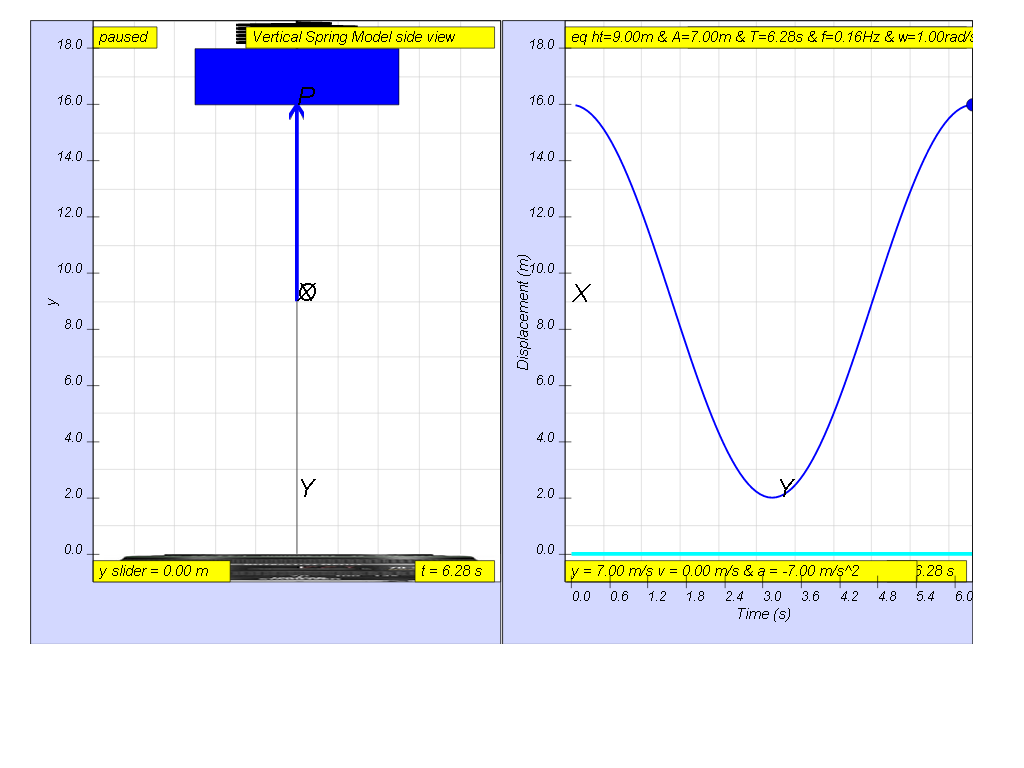
A mass undergoes an oscillation where the maximum/minimum amplitude is 16.0 m mark and 2.0 m mark on a rule respectively. It was found that the particle only takes 3.14 s to move from X = 16.0 m to Y = 2.0 m during the oscillations as shown. Determine the   
(a)     amplitude,      
(b)     period,     
(c)     frequency,      
(d)     angular frequency, of the oscillations.
[ 7.0 m, 6.28 s, 0.166 Hz, 1.00 rad/s ]

1.2.12.1Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/91

1.2.12.2 Inquiry

Q1: run model with different mass m and spring constant k to explore different amplitude x₀, period T, frequency f and angular frequency ω.
Q2: setup your own initial conditions and test your understanding of with is the physical meaning of amplitude x₀, period T, frequency f and angular frequency ω.

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM162/SHM162_Simulation.xhtml

 Apps

https://play.google.com/store/apps/details?id=com.ionicframework.shm161app280927&hl=en

end faq

{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}