About
1.3 a) Variation with time of energy in simple harmonic motion
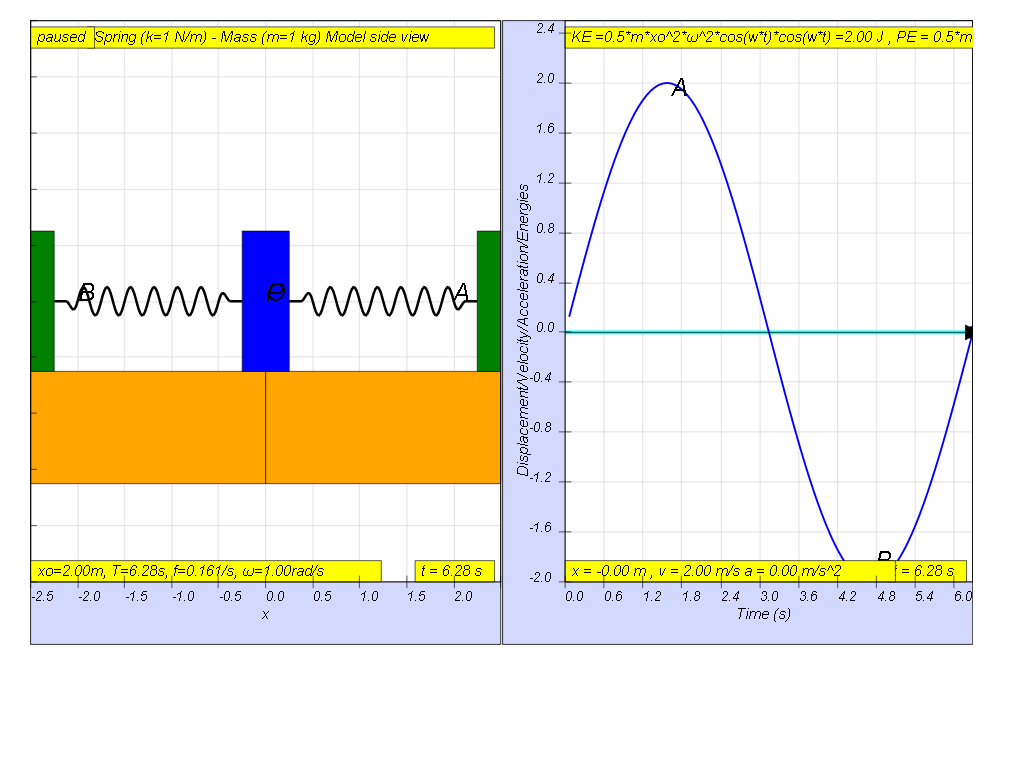
If the variation with time of displacement is as shown, then the energies should be drawn as shown.
recalling Energy formula
PE = ½ k x2
in terms of time t,
x = x0 sin(ωt)
differentiating with t gives
v = v0 cos (ωt)
therefore, KE = ½ m v2= ½ m (v0 cos (ωt))2= ½ m (x02ω2)cos (ωt))2similarly
PE = ½ k x2= ½ (mω2 )(x0 sin (ωt))2= ½ m (x02ω2 )sin (ωt))2
therefore total energy is a constant value in the absence of energy loss due to drag (resistance)
TE = KE + PE = ½ m (x02ω2 )[cos2(ωt)
+ sin2(ωt))] = ½ m (x02ω2)
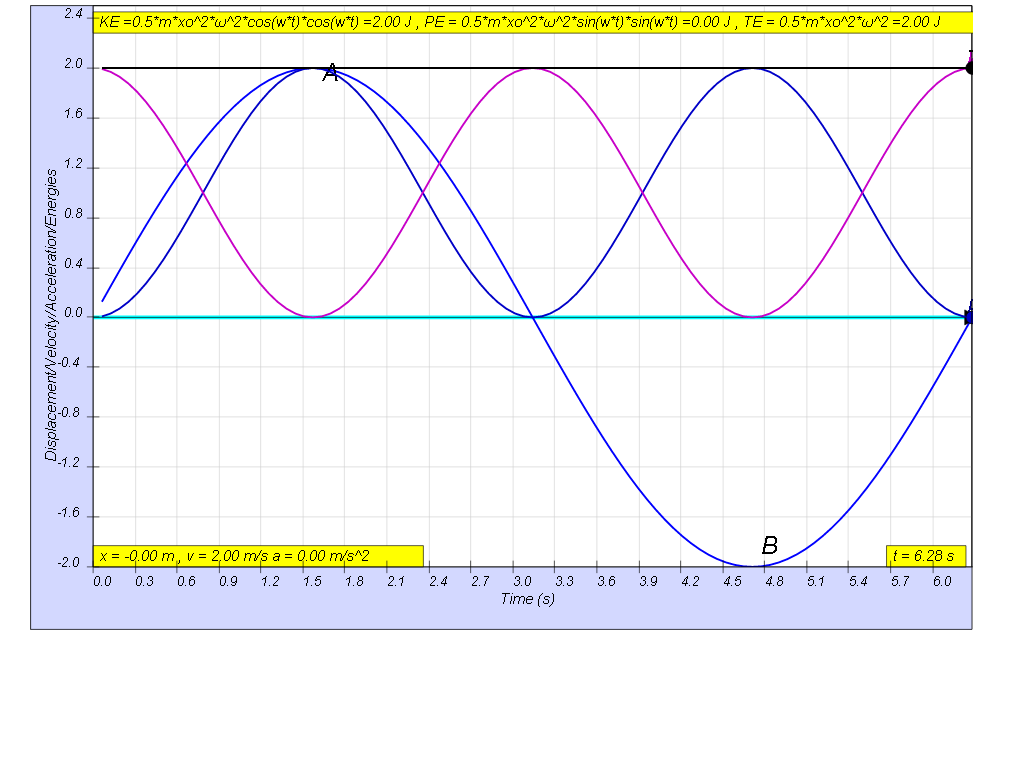
this is how the x vs t looks together of the energy vs t graphs
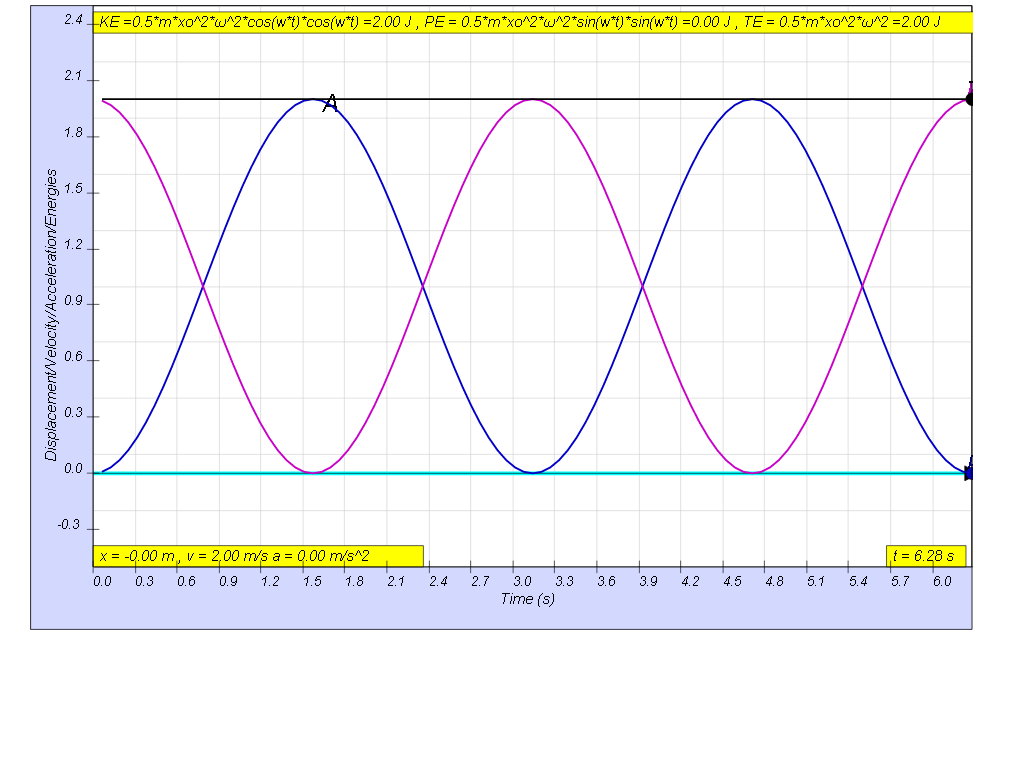
1.3.1 Summary
the table shows some of the common values| general energy formula | SHM energy formula | when t = 0 | when t = T/4 | when t = T/2 | when t = 3T/4 | when t = T |
| KE = ½ m v2 | ½ m (x02ω2)cos (ωt))2 | ½ m (x02ω2) | 0 | ½ m (x02ω2) | 0 | ½ m (x02ω2) |
| PE = ½ k x2 | ½ m (x02ω2)cos (ωt))2 | 0 | ½ m (x02ω2) | 0 | ½ m (x02ω2) | 0 |
| TE = KE + PE | TE = ½ m (x02ω2) | ½ m (x02ω2) | ½ m (x02ω2) | ½ m (x02ω2) | ½ m (x02ω2) | ½ m (x02ω2) |
1.3.2 Model:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits
 This email address is being protected from spambots. You need JavaScript enabled to view it.
This email address is being protected from spambots. You need JavaScript enabled to view it.
Briefing Document: ⚛️Simple Harmonic Motion and Energy Variation
Document Source: Excerpts from "10.3 Variation with Time of Energy in Simple Harmonic Motion JavaScript HTML5 Applet Simulation Model - Open Educational Resources / Open Source Physics @ Singapore"
Date: 2024-06-27
1. Overall Theme: Energy in Simple Harmonic Motion (SHM)
The primary focus of this resource is to explain and demonstrate how energy varies with time in a system undergoing simple harmonic motion. This is achieved through a JavaScript HTML5 applet simulation, allowing for an interactive learning experience. The resource emphasizes the relationship between kinetic energy (KE), potential energy (PE), and total energy (TE) in SHM.
2. Key Concepts and Ideas
- Simple Harmonic Motion (SHM): The document assumes the reader has a basic understanding of SHM, which is described as a periodic motion where the restoring force is directly proportional to the displacement. It uses a standard spring-mass system as a model.
- Energy Forms in SHM: The resource clearly defines and differentiates between KE, PE, and TE in the context of SHM:
- Kinetic Energy (KE): "KE = ½ m v²" - The energy of motion, dependent on the mass (m) and velocity (v) of the object.
- Potential Energy (PE): "PE = ½ k x²" - The energy stored due to the position of the object, dependent on the spring constant (k) and displacement (x). Note that k in this case has been rewritten in terms of mass and angular frequency, k = mω².
- Total Energy (TE): "TE = KE + PE" - The sum of KE and PE, which is a constant value in an ideal system without energy loss.
- Mathematical Representation:
- Displacement (x): "x = x₀ sin(ωt)" - The displacement varies sinusoidally with time (t), where x₀ is the amplitude, and ω is the angular frequency.
- Velocity (v): "v = v₀ cos (ωt)" - The velocity also varies sinusoidally, with a phase difference compared to the displacement.
- Kinetic Energy (KE) as function of time: "KE = ½ m v²= ½ m (v₀ cos (ωt))²= ½ m (x₀²ω²)cos² (ωt))"
- Potential Energy (PE) as a function of time: "PE = ½ k x²= ½ (mω² )(x₀ sin (ωt))²= ½ m (x₀²ω² )sin²(ωt))"
- Total Energy (TE): "TE = KE + PE = ½ m (x₀²ω² )[cos²(ωt) + sin²(ωt))http://iwant2study.org/ospsg/index.php/80" target="_blank" rel="noopener noreferrer" style="box-sizing: border-box; color: rgb(0, 102, 204); text-decoration: underline;">http://iwant2study.org/ospsg/index.php/80.
- Apps: Links to Android apps are also provided, showcasing portability of the simulations across different platforms.
4. Additional Resources and Context
- Part of a Larger Collection: The resource is part of a larger collection of "Open Educational Resources / Open Source Physics @ Singapore." This suggests that it's part of a wider effort to provide free and accessible educational materials.
- Specific Topics Covered: There is a large number of interactive simulations listed on the page, covering a wide array of topics such as: Kinematics, Newtonian Mechanics, Simple Harmonic Motion, Gravitation, Electromagnetism, and other general physics topics. This shows the breadth of the content provided by this project.
- WebEJS Authoring Tool: The document also mentions the use of the Web Easy JavaScript Simulation (WebEJS) authoring tool, showcasing that the resources were created using this particular tool.
- Various Projects and Workshops: The page also provides a huge list of WebEJS related projects and workshops, showcasing the ongoing nature of the resource creation and improvement.
- Focus on Interactive Learning: The emphasis on applets, simulations, and interactive models highlights the intention to engage students in a more hands-on way.
- Creative Commons License: The resources are licensed under a Creative Commons Attribution-Share Alike 4.0 Singapore License, allowing for sharing and adaptation for non-commercial use.
5. Target Audience
- The resource is likely aimed at Junior College or equivalent level students studying physics, specifically covering the topic of simple harmonic motion.
- It could also be used by teachers to enhance their lessons on oscillations and energy.
6. Summary
This document provides a comprehensive and interactive learning resource for understanding the energy dynamics within simple harmonic motion. It uses mathematical formulas, clear explanations, and an accessible simulation to elucidate the interchange between kinetic and potential energy while showcasing the conservation of total energy in an ideal system. The platform offers a wide range of resources created using the WebEJS tool, catering to various topics in physics and mathematics. The resources are openly licensed, promoting accessibility and educational innovation.
Simple Harmonic Motion and Energy: A Study Guide
Quiz
- What is the relationship between kinetic energy (KE) and potential energy (PE) in simple harmonic motion (SHM)?
- Describe how displacement (x) varies with time (t) in SHM, referencing the provided formula.
- How is velocity (v) related to time (t) in the context of SHM, based on the given formulas?
- Explain how the total energy (TE) in SHM behaves in the absence of energy loss due to resistance.
- What is the mathematical expression for kinetic energy (KE) in SHM, as shown in the text?
- What is the mathematical expression for potential energy (PE) in SHM, as shown in the text?
- What is the mathematical expression for total energy (TE) in SHM, as shown in the text?
- According to the summary table, what are the KE, PE, and TE values at t=0?
- According to the summary table, what are the KE, PE, and TE values at t=T/4?
- According to the summary table, what are the KE, PE, and TE values at t=T/2?
Quiz Answer Key
- In SHM, KE and PE are constantly interchanging. When one is at its maximum, the other is at its minimum, and the total energy remains constant (in the absence of resistance).
- Displacement (x) varies sinusoidally with time (t), as described by the formula x = x₀ sin(ωt), where x₀ is the amplitude and ω is the angular frequency.
- Velocity (v) varies cosinusoidally with time (t), as described by the formula v = v₀ cos(ωt), where v₀ is the maximum velocity.
- In the absence of energy loss, the total energy (TE) in SHM remains constant over time, meaning the sum of KE and PE at any point is the same.
- The mathematical expression for kinetic energy (KE) in SHM is KE = ½ m (x₀²ω²)cos²(ωt), where m is the mass, x₀ is the amplitude, and ω is the angular frequency.
- The mathematical expression for potential energy (PE) in SHM is PE = ½ m (x₀²ω²)sin²(ωt), where m is the mass, x₀ is the amplitude, and ω is the angular frequency.
- The mathematical expression for total energy (TE) in SHM is TE = ½ m (x₀²ω²), where m is the mass, x₀ is the amplitude, and ω is the angular frequency.
- At t = 0, KE = ½ m (x₀²ω²), PE = 0, and TE = ½ m (x₀²ω²).
- At t = T/4, KE = 0, PE = ½ m (x₀²ω²), and TE = ½ m (x₀²ω²).
- At t = T/2, KE = ½ m (x₀²ω²), PE = 0, and TE = ½ m (x₀²ω²).
Essay Questions
- Discuss the energy transformations in simple harmonic motion. Include in your essay a discussion of the relationship between kinetic energy, potential energy, and total energy throughout one complete cycle, citing the equations that demonstrate this relationship.
- Explain how the provided formulas for displacement, velocity, kinetic energy, and potential energy demonstrate the fundamental principles of SHM. Further, discuss how these equations change if the system were under some resistance or drag and no longer a closed system.
- Using the provided summary table, analyze the energy distribution (KE, PE, and TE) at different time points (t=0, T/4, T/2, 3T/4, T) in SHM. Explore what these different stages of the cycle tell us about the overall motion of the system.
- Evaluate the significance of the constant total energy (TE) in the context of SHM. How does this principle relate to the conservation of energy, and what conditions are necessary for it to hold true?
- The simulation in the text provides multiple interactive applets to investigate SHM. Design an experiment using one of the applets to investigate a particular aspect of SHM, and describe the goals, procedure, and expected results.
Glossary of Key Terms
- Simple Harmonic Motion (SHM): A type of periodic motion where the restoring force is directly proportional to the displacement and acts in the opposite direction. Characterized by oscillation.
- Kinetic Energy (KE): The energy possessed by an object due to its motion. In SHM, it is expressed as KE = ½ m v².
- Potential Energy (PE): The energy possessed by an object due to its position or condition. In SHM, it is often stored as elastic potential energy (PE = ½ k x²).
- Total Energy (TE): The sum of kinetic and potential energy in a system. In ideal SHM, this remains constant over time.
- Displacement (x): The distance of an oscillating object from its equilibrium position.
- Velocity (v): The rate of change of displacement with respect to time.
- Amplitude (x₀): The maximum displacement of an oscillating object from its equilibrium position.
- Angular Frequency (ω): A measure of the rate of oscillation, related to the period (T) by ω = 2π/T
- Time (t): A measure of the duration in which an event occurs. In the context of SHM, t is related to the displacement, velocity, and energy at different points in the oscillation cycle.
- Period (T): The duration of one complete oscillation cycle.
Apps
https://play.google.com/store/apps/details?id=com.ionicframework.shm17app307408&hl=en
Other resources
Frequently Asked Questions about Simple Harmonic Motion (SHM) and Energy
- What is Simple Harmonic Motion (SHM), and what kind of system exhibits it?
- Simple Harmonic Motion (SHM) is a type of periodic motion where the restoring force is directly proportional to the displacement and acts in the opposite direction of that displacement. A classic example is a mass attached to a spring, where the spring exerts a force pulling the mass back to its equilibrium position. This restoring force causes the mass to oscillate back and forth, creating SHM. The SHM simulation models show horizontal spring-mass systems which are ideal for visualizing the energy changes during SHM.
- How does displacement vary with time in SHM?
- The displacement of an object undergoing SHM varies sinusoidally with time. This means it can be represented by a sine or cosine function. Specifically, the displacement x as a function of time t can be described by x = x₀ sin(ωt), where x₀ is the amplitude (maximum displacement), and ω is the angular frequency. The velocity varies as v = v₀ cos (ωt), with v₀ as the maximum velocity, showing a 90 degree phase difference with the displacement.
- What is the relationship between kinetic energy (KE) and potential energy (PE) in SHM?
- In SHM, there is a continuous transfer of energy between kinetic and potential energy. Kinetic energy is the energy of motion and is at maximum when the mass passes through equilibrium position (zero displacement) and is zero at maximum displacement. Potential energy is stored energy and in the spring-mass system, is maximum at the maximum displacement and zero when passing through equilibrium. At any given time, the total energy is the sum of KE and PE. When KE is at its maximum, PE is at its minimum and vice-versa; when displacement is maximum, KE is zero and PE is maximum.
- How do the equations for Kinetic Energy (KE) and Potential Energy (PE) look in SHM with respect to time?
- The Kinetic Energy (KE) is given by KE = ½ m v² = ½ m (x₀²ω²)cos²(ωt) where m is the mass, x₀ is the amplitude, and ω is the angular frequency. Potential Energy (PE) is given by PE = ½ k x² = ½ mω² (x₀ sin(ωt))² = ½ m (x₀²ω²)sin²(ωt) where k is the spring constant and x is the displacement at a given time t. These equations clearly show how the kinetic and potential energies are changing as a function of time through the cosine-squared and sine-squared functions, respectively.
- What is the total energy in SHM, and how does it change over time?
- The total energy in SHM is the sum of kinetic and potential energies, and it remains constant (assuming no energy loss). This total energy is given by TE = KE + PE = ½ m (x₀²ω²). The fact that this value does not include the variable t shows that the total energy is constant, meaning it does not vary with time and it's always proportional to the square of the amplitude (x₀²) and angular frequency (ω²).
- How can these concepts be visualized, and what tools are available?
- Interactive simulations, like the JavaScript HTML5 applet models described, are an excellent way to visualize these concepts. These models allow you to observe the relationship between displacement, velocity, kinetic energy, and potential energy as they change in real-time during SHM. Many of these simulations are readily available on websites like iwant2study.org and can be embedded on other sites.
- Where can I find more resources or tools related to SHM?
- The provided document has many links to various types of educational resources. These resources include Java and Javascript-based interactive simulations, GeoGebra applets, applications for Android and iOS, and models that demonstrate SHM. It suggests looking at iwant2study.org or specific links mentioned, as well as exploring other links for more related models for understanding SHM and other related physics concepts. You can also find apps for mobile devices in the Google Play Store, and videos on Youtube.
- Are there any limitations to these SHM models?
- The provided model highlights that the total energy is constant in the absence of energy loss due to drag (resistance). This means, in real systems, energy is not perfectly conserved because of factors like air resistance, which will dissipate energy. These interactive simulation models are a good way to explore the concepts of simple harmonic motion assuming an idealized (and simpler) case. Many simulations are presented as ways of exploring and modeling real physical systems to gain understanding. The list of resources point to a large variety of additional models, such as those that deal with drag and resistance, that can demonstrate more realistic models of the world.
- Details
- Parent Category: 02 Newtonian Mechanics
- Category: 09 Oscillations
- Hits: 9576