About
1.7 Forced Oscillations and Resonance LO (j)
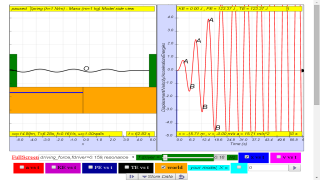
When a system performs oscillations without any applied force, the frequency of the oscillation is a characteristic of the system and is called the natural frequency, fo . In the example above, the fo = 0.161 Hz.
1.7.1 Spring Mass System initially at Rest
Consider a spring mass system initially at rest.
1.7.1.1 No driving force
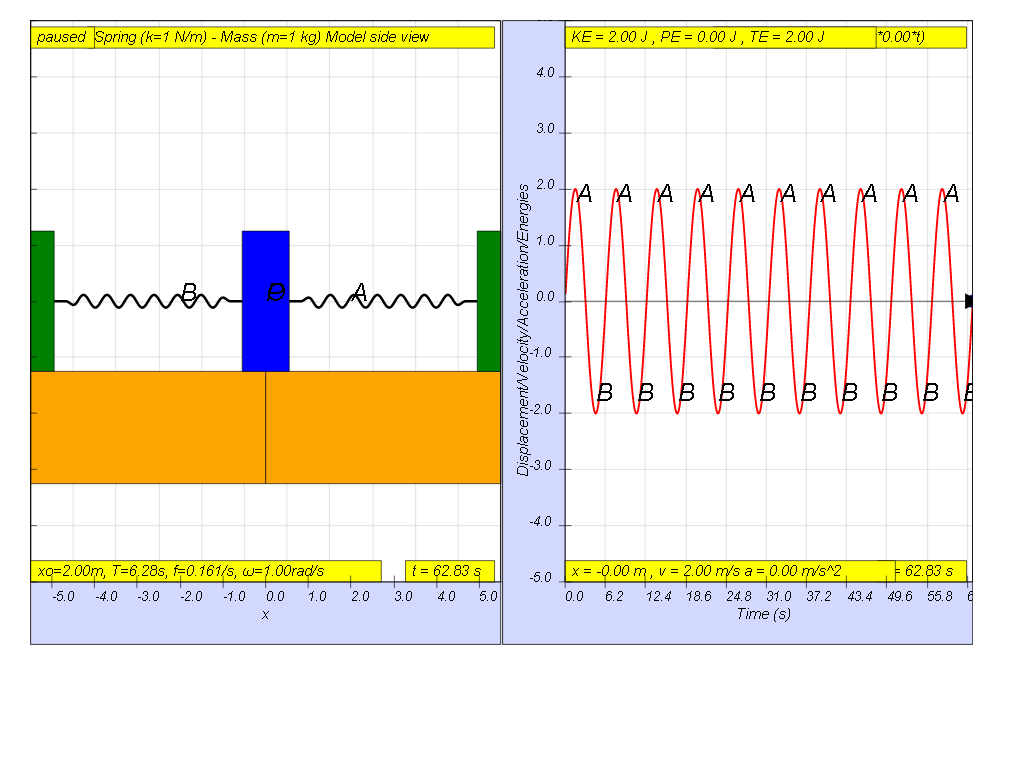
When the driving force is at f = 0, that means the driving force is Fdriver = (0.5)sin(2π f t ) = 0.
the result is as shown on the picture where x = 0 for all time since there is no external driving force acting on the system.
1.7.1.2 Slow driving force
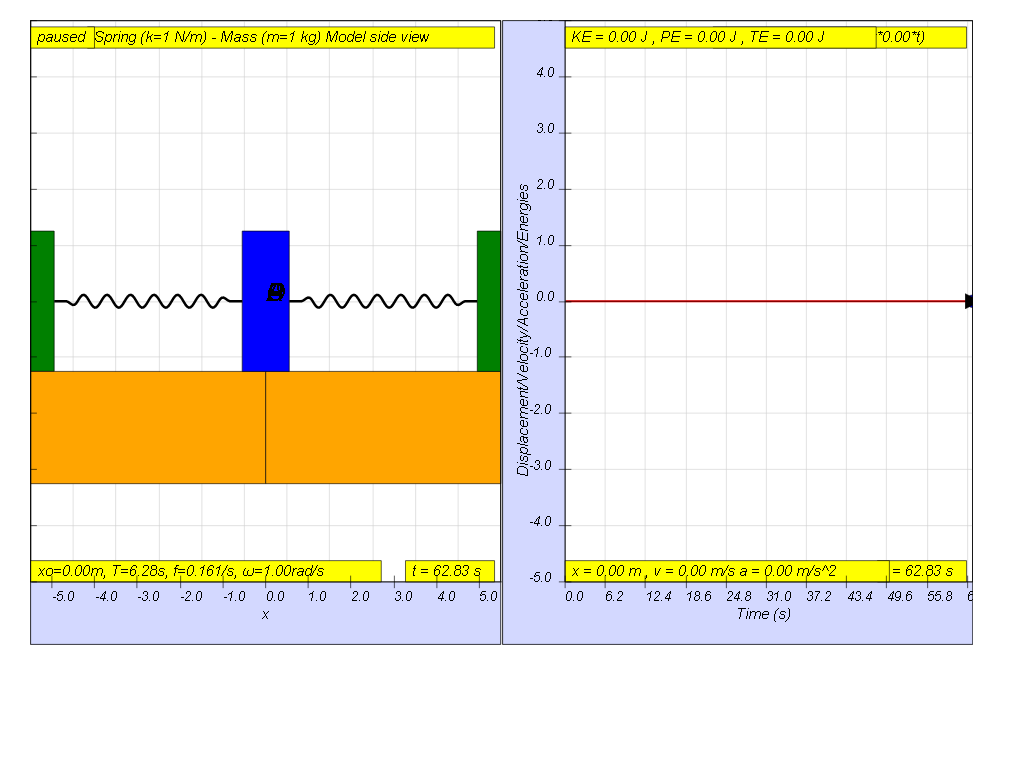
However, when f = 0.1 , the Fdriver = (0.5)sin(2π (0.1) t ), it results in a motion that seems to irregular reaching a maximum amplitude of A and B (see picture).
1.7.1.3 Driving force equal Natural frequency
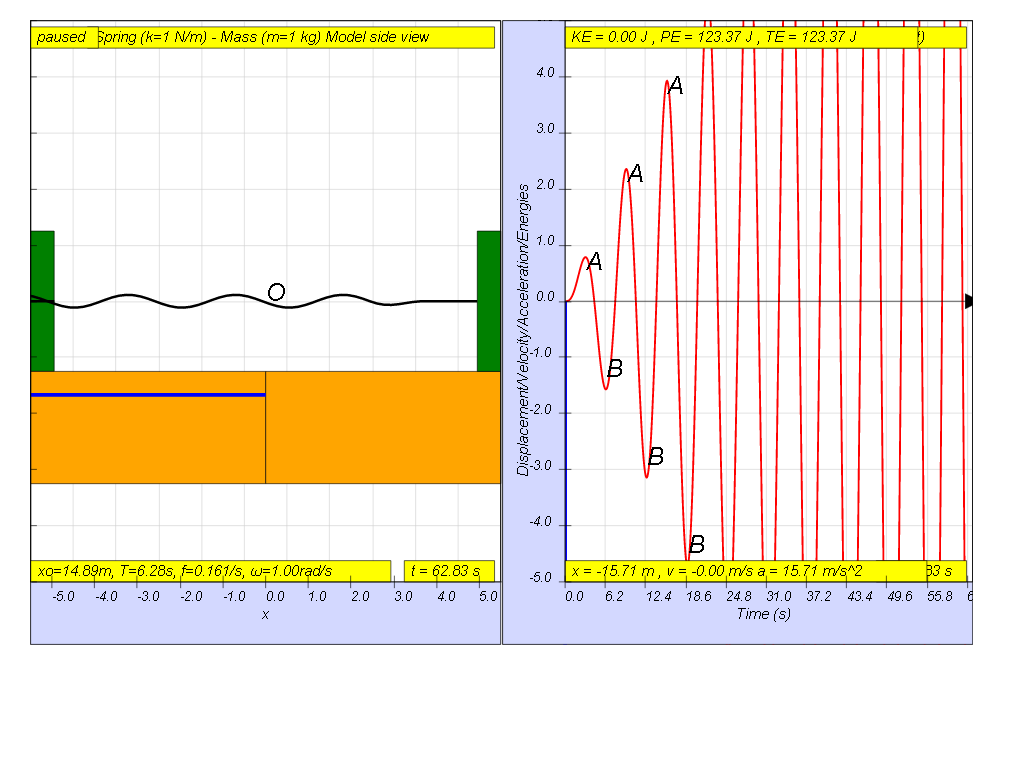
However, when f = 0.159 , the Fdriver = (0.5)sin(2π (0.159) t ), it results in a motion that seems to increase to a very large maximum amplitude of A and B (see picture, when t = 55.8, A and B are greater than the screen display height). Theoretically, is should be infinitely large.
1.7.1.4 Driving force greater than Natural frequency
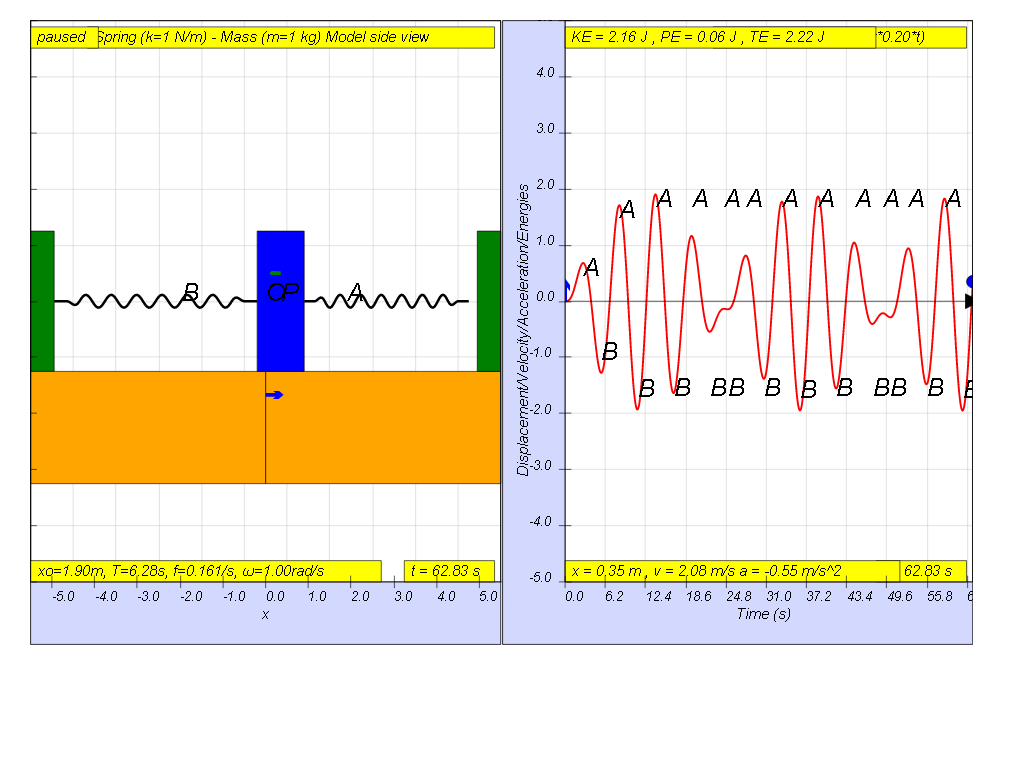
However, when f = 0.2 , the Fdriver = (0.5)sin(2π (0.2) t ), it results in a motion that seems to also reach some smaller maximum amplitude of A and B (see picture reaching about 1.8 ).
1.7.1.5 Driving force much greater than Natural frequency
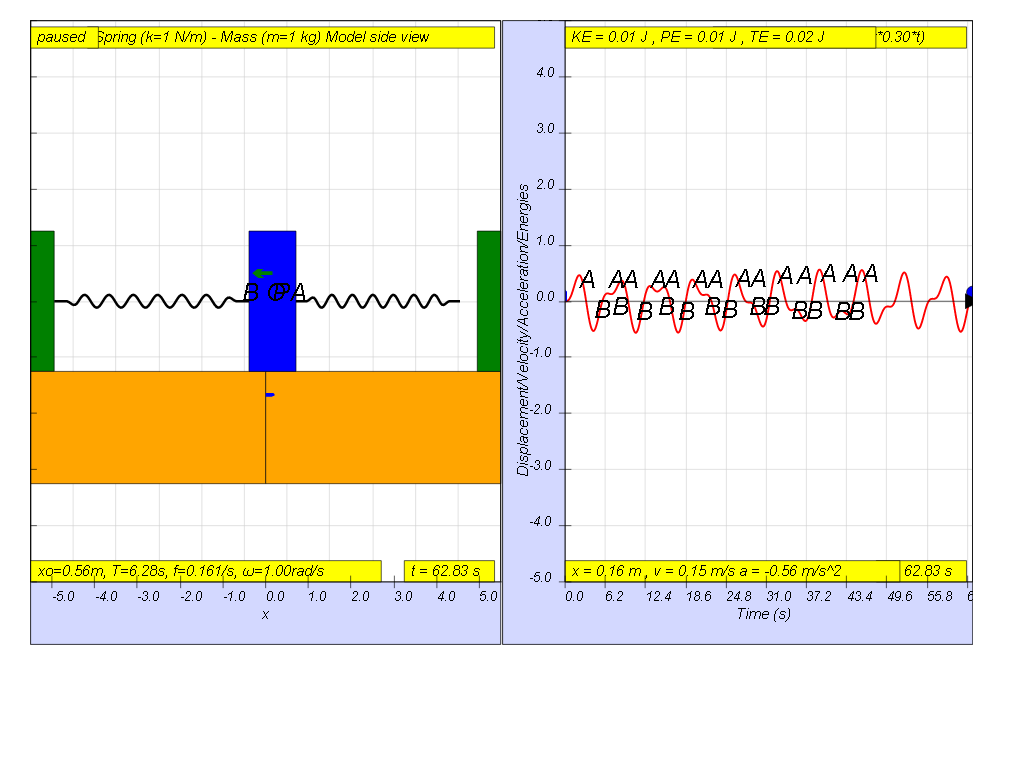
However, when f = 0.3 , the Fdriver = (0.5)sin(2π (0.3) t ), it results in a motion that seems to also reach rather maximum amplitude of A and B (see picture reaching about 0.5 ).
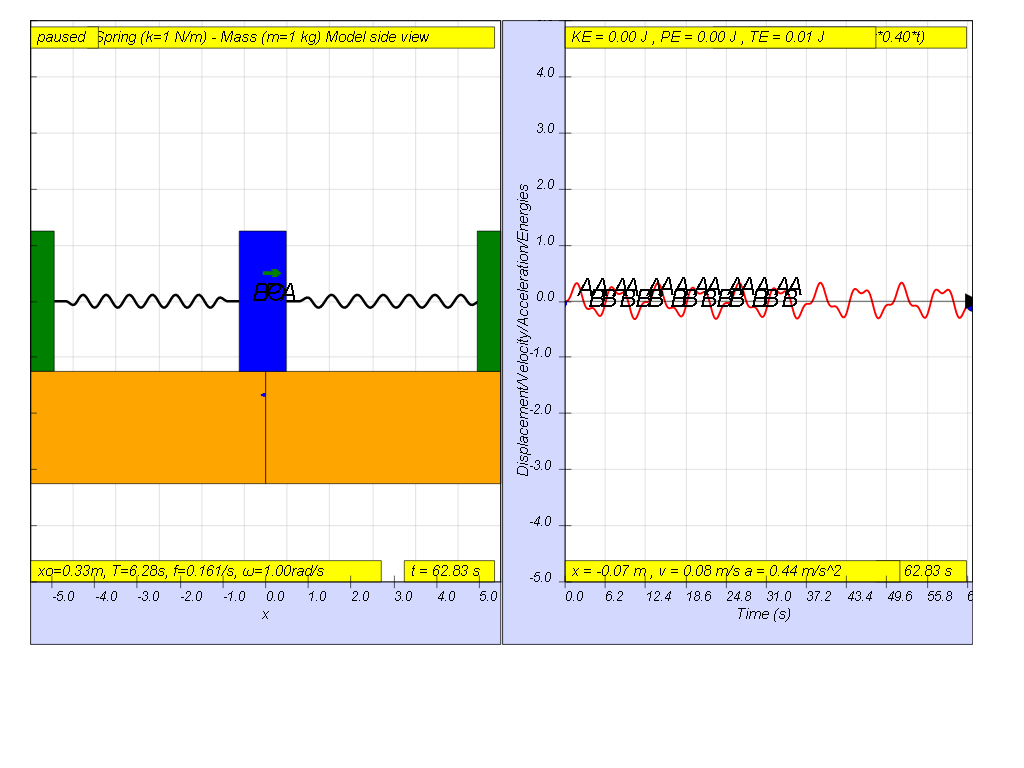
Lastly, when f = 0.4 , the Fdriver = (0.5)sin(2π (0.4) t ), it results in a motion that seems to also reach even smaller maximum amplitude of A and B (see picture reaching about 0.3 ).
These oscillations in which a periodic force is imposed are called forced resonance. Systems will then some what influenced to vibrate at the frequency of the periodic force, f, but only when f = fo = 0.161 Hz , in this example, the maximum amplitude is the greatest happens in this case when damping is zero as has similar maximum amplitude effects for different damping levels occurring near f = fo
1.7.2 Examples include the
1) Vibrations of a pendulum clock.
2) Vibrations of a tuning fork when exposed to the periodic force of a sound wave.
3) Vibration of a bridge under the influence of marching soldiers or periodic wind.
1.7.3 Model:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits
 This email address is being protected from spambots. You need JavaScript enabled to view it.
This email address is being protected from spambots. You need JavaScript enabled to view it.
Briefing Document: ⚛️Forced Oscillations and Resonance Simulation
1. Overview
This document analyzes an HTML5 applet simulation model focused on forced oscillations and resonance, primarily within a spring-mass system. The resource is provided by "Open Educational Resources / Open Source Physics @ Singapore." This simulation is designed as an educational tool, accessible on various platforms (Windows, macOS, Linux, Android, iOS, and Chromebooks), and is part of a broader collection of physics simulations.
2. Key Concepts
- Natural Frequency (f₀): The inherent frequency at which a system oscillates when not driven by an external force. In the provided example, f₀ = 0.161 Hz. This is a characteristic of the system.
- "When a system performs oscillations without any applied force, the frequency of the oscillation is a characteristic of the system and is called the natural frequency, fo. In the example above, the fo = 0.161 Hz."
- Forced Oscillations: Oscillations that occur when an external periodic force is applied to a system. The frequency of this external force is denoted as f.
- "These oscillations in which a periodic force is imposed are called forced resonance."
- Driving Force (Fdriver): In this simulation, the driving force is represented by Fdriver = (0.5)sin(2π f t ). The amplitude of the driving force is 0.5, while f is the driving frequency.
- Resonance: A phenomenon where the amplitude of oscillations becomes very large when the driving frequency (f) approaches the natural frequency (f₀) of the system. The simulation demonstrates this dramatically.
- "Systems will then some what influenced to vibrate at the frequency of the periodic force, f , but only when f = fo = 0.161 Hz , in this example, the maximum amplitude is the greatest happens in this case when damping is zero as has similar maximum amplitude effects for different damping levels occurring near f = fo"
3. Simulation Demonstrations
The simulation systematically explores the effect of varying the driving frequency (f) on the behavior of a spring-mass system:
- No Driving Force (f = 0): No motion is observed since no external force is applied.
- "When the driving force is at f = 0, that means the driving force is Fdriver = (0.5)sin(2π f t ) = 0. the result is as shown on the picture where x = 0 for all time since there is no external driving force acting on the system."
- Slow Driving Force (f < f₀): The system oscillates, reaching a moderate amplitude. In the example when f = 0.1, the motion is "irregular" with a modest maximum amplitude.
- Driving Force Equal to Natural Frequency (f ≈ f₀): The system exhibits resonance, with a significantly large (theoretically infinite in the absence of damping) amplitude. When f = 0.159 (very close to f₀), the system oscillates with a very large amplitude.
- "However, when f = 0.159 , the Fdriver = (0.5)sin(2π (0.159) t ), it results in a motion that seems to increase to a very large maximum amplitude of A and B (see picture, when t = 55.8, A and B are greater than the screen display height). Theoretically, is should be infinitely large."
- Driving Force Greater than Natural Frequency (f > f₀): The system still oscillates but with a smaller amplitude, and this is further reduced as the driving frequency increases further.
- At f = 0.2, the amplitude is smaller than resonance.
- At f = 0.3, the amplitude is even smaller
- At f = 0.4, the amplitude is smallest of those described above
4. Real-World Examples of Resonance
The document provides real-world examples to illustrate the concept of forced oscillations and resonance:
- Vibrations of a pendulum clock.
- Vibrations of a tuning fork exposed to sound waves.
- Vibrations of a bridge under the influence of marching soldiers or periodic wind.
- *"1) Vibrations of a pendulum clock.
- Vibrations of a tuning fork when exposed to the periodic force of a sound wave.
- Vibration of a bridge under the influence of marching soldiers or periodic wind."*
5. Technical Details & Access
- Simulation Link: The simulation can be embedded via an iframe using the URL: https://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM23/SHM23_Simulation.xhtml
- App Availability: The simulation is also available as a mobile application on the Google Play store.
- Platform Accessibility: The resource is designed to be accessed across many platforms.
- Additional Resources: The page links to many other physics and math resources and simulation applets, showcasing a wide range of learning materials.
6. Educational Value
This simulation serves as an interactive tool for understanding:
- The concept of natural frequency.
- The effect of a driving force on an oscillating system.
- The phenomenon of resonance and how it is related to matching the driving frequency to the natural frequency.
- Real-world applications of resonance.
- The effect of damping in reducing the effects of resonance.
7. Key Takeaways
- Resonance occurs when the driving force's frequency matches a system's natural frequency, leading to large amplitude oscillations.
- The amplitude of oscillations is maximized at resonance and decreases as the driving frequency deviates from the natural frequency.
- This model is a valuable tool for exploring these concepts interactively in a physics classroom.
- The website provides other interactive educational content covering a very wide range of topics.
- This material is open source, under a Creative Commons license.
This briefing document encapsulates the core information and ideas presented in the provided source about forced oscillations and resonance. It provides a basis for understanding the simulation and its educational value.
Forced Oscillations and Resonance Study Guide
Quiz
- What is the natural frequency of a system, and how is it determined?
- Describe what happens to a spring-mass system when the driving force is zero.
- Explain the motion of a spring-mass system when subjected to a slow driving force, mentioning the key characteristics of the motion
- How does the amplitude of oscillation change when the driving force frequency approaches the natural frequency?
- What is the theoretical maximum amplitude of oscillation when the driving frequency equals the natural frequency?
- Describe the amplitude of oscillation when the driving frequency is greater than the natural frequency.
- How does a driving frequency that is much greater than the natural frequency affect the amplitude of oscillation?
- What are forced oscillations?
- What is resonance and under what conditions does it occur?
- Give two examples of real-world systems that exhibit forced oscillations.
Answer Key
- The natural frequency of a system is the characteristic frequency at which it oscillates without any applied external force. It is determined by the system's physical properties, such as mass and spring constant in the case of a spring-mass system.
- When the driving force is zero, the spring-mass system remains at rest with no motion. This is because there is no external force to cause displacement or oscillation.
- When subjected to a slow driving force, the spring-mass system exhibits irregular motion, with a smaller maximum amplitude of oscillation. The motion is neither smooth nor constant.
- As the driving force frequency approaches the natural frequency, the amplitude of oscillation increases significantly. This increase in amplitude is a key characteristic of resonance.
- Theoretically, when the driving frequency equals the natural frequency, the maximum amplitude of oscillation should be infinitely large if there is no damping.
- When the driving frequency is greater than the natural frequency, the amplitude of oscillation decreases compared to the resonant case, but the system still exhibits some motion.
- A driving frequency that is much greater than the natural frequency results in a relatively small maximum amplitude of oscillation. The system's response is minimal in this case.
- Forced oscillations occur when a periodic external force is applied to a system, causing it to vibrate at the frequency of the applied force, which may or may not be equal to the natural frequency of the system.
- Resonance is a phenomenon that occurs when the driving force frequency matches the natural frequency of the system, resulting in a large increase in the amplitude of oscillations, particularly when damping is minimal.
- Two real-world examples of forced oscillations include the vibrations of a pendulum clock and the vibration of a bridge under the influence of marching soldiers or periodic wind.
Essay Questions
- Explain how the relationship between driving frequency and natural frequency impacts the amplitude of oscillation in a spring-mass system. Use specific examples from the provided source to support your claims.
- Discuss the practical implications of resonance in real-world engineering scenarios. Provide examples of how understanding and controlling resonance are crucial in design and safety.
- Compare and contrast the effects of a driving force at frequencies below, equal to, and above the natural frequency on a system’s oscillation, including amplitude, and explain why these differences occur.
- Describe in detail the phenomenon of forced resonance using examples from the text, specifically discussing its effects on oscillation amplitudes when damping is zero, or other damping levels.
- Analyze the significance of the natural frequency of a system and how its understanding is essential for preventing catastrophic events such as bridge collapses.
Glossary of Key Terms
Natural Frequency (fo): The frequency at which a system oscillates freely without any external force applied. This is a characteristic property of the system.
Driving Force: An external, periodic force applied to a system, causing it to oscillate. It is defined by its amplitude and frequency.
Forced Oscillations: Oscillations that occur when a system is subjected to a periodic external force. The system is forced to vibrate at the frequency of the applied force.
Resonance: A phenomenon that occurs when the frequency of the driving force matches the natural frequency of a system, leading to a significant increase in the amplitude of oscillations.
Amplitude: The maximum displacement or extent of an oscillation from its equilibrium position. In this context, the peak displacement reached by the oscillating mass.
Damping: The reduction in the amplitude of an oscillation due to energy dissipation or friction. It causes oscillations to gradually decrease over time.
Apps
https://play.google.com/store/apps/details?id=com.ionicframework.shm23app540489&hl=en
Frequently Asked Questions: Forced Oscillations and Resonance
- What is natural frequency (f₀) in the context of oscillations? The natural frequency (f₀) is the inherent frequency at which a system will oscillate when disturbed without any external driving force. It's a characteristic of the system itself, determined by its physical properties like mass and stiffness in a spring-mass system. For the example in the source, the natural frequency of the system is f₀= 0.161 Hz.
- What happens when there is no driving force applied to an oscillating system? When no driving force is applied (f=0), a system initially at rest will remain at rest and will not oscillate. The driving force is Fdriver = (0.5)sin(2π f t ). When f=0, Fdriver becomes 0. Thus there is no external force acting upon the system, it will remain with x=0 for all times.
- How does a slow driving force affect an oscillating system? When a slow driving force is applied (e.g., f=0.1 Hz), the system begins to oscillate, but with a seemingly irregular motion, and reaching a maximum amplitude. The resulting amplitude is neither very large nor very small.
- What is forced resonance, and how does it occur? Forced resonance occurs when a periodic driving force is applied to an oscillating system. The system is forced to vibrate at the frequency of the external driving force (f). The amplitude of the oscillation depends on the driving frequency in relation to the system's natural frequency (f₀). When the driving frequency equals the natural frequency (f=f₀), the amplitude of the oscillation reaches the maximum and becomes very large, a phenomenon called resonance.
- What happens when the driving frequency equals the natural frequency? When the driving frequency (f) of the external force is equal to the natural frequency (f₀) of the system, resonance occurs. This results in a dramatic increase in the amplitude of the oscillations. In the example provided, when f = 0.159 Hz (close to f₀), the amplitude theoretically becomes infinitely large in the absence of damping, practically meaning the oscillation amplitude becomes much larger than other frequencies.
- What happens when the driving frequency is greater than or much greater than the natural frequency? When the driving frequency (f) is greater than the natural frequency (f₀), the system will oscillate, but with a lower amplitude than at resonance. As the driving frequency increases further and much higher than f₀, the amplitude of the oscillations becomes smaller. The system oscillates somewhat at the driving frequency but with a smaller maximum amplitude. For instance, driving forces at frequencies of f = 0.2, 0.3, and 0.4 Hz result in decreasing maximum amplitudes.
- What are some real-world examples of forced oscillations and resonance? Examples include the vibrations of a pendulum clock, a tuning fork vibrating when exposed to a sound wave, and the vibrations of a bridge caused by marching soldiers or periodic wind. These examples highlight that resonance can be both useful (e.g., in musical instruments) and potentially destructive (e.g., bridge collapses).
- How does damping affect forced oscillations and resonance? The source mentions that when damping is zero, the effect of maximum amplitude near f = f₀ is more obvious and can be theoretically infinite. In reality, damping is always present. Damping reduces the amplitude of oscillations at all driving frequencies, but particularly reduces the maximum amplitude achieved at resonance. The overall effect of damping is to reduce the maximum amplitude.
- Details
- Parent Category: 02 Newtonian Mechanics
- Category: 09 Oscillations
- Hits: 15211