
About
For Teachers
- motionofpersonning.mp4
- .DS_Store
Credits
Author: This email address is being protected from spambots. You need JavaScript enabled to view it.
Contact: This email address is being protected from spambots. You need JavaScript enabled to view it.
Briefing Doc: Tracker Motion of Person Progressive Model Building Pedagogy
Source: Excerpts from "Tracker Motion of Person Progressive Model Building Pedagogy by NJC Ning Hwee Tiang" on Open Educational Resources / Open Source Physics @ Singapore.
Author: Ning Hwee Tiang from National Junior College (NJC)
Collaborator: Lookang Lawrence Wee
Summary: This resource utilizes the Tracker software to analyze the motion of a person and progressively build computational models that accurately represent the observed motion. The pedagogy emphasizes the iterative nature of scientific modeling and allows students to visualize and understand the relationship between forces, velocity, and acceleration.
Key Themes:
- Progressive Model Building: The core theme involves starting with a simple model (no force) and gradually adding complexity to better match the real-world data captured in the video. This approach highlights the iterative nature of scientific modeling, where initial assumptions are refined based on experimental observations.
- Newton's Laws of Motion: The models demonstrate the application of Newton's laws, particularly the second law (F=ma) and the first law (inertia). Students can observe how a net force results in acceleration and how an object in motion stays in motion at constant velocity unless acted upon by a force.
- Data Analysis and Visualization: Tracker facilitates data analysis by providing tools to track the position of an object over time. This data is then used to derive parameters for the models, such as initial velocity and acceleration. Visualization of both the observed motion and the simulated motion allows for a direct comparison and assessment of the model's accuracy.
- Computational Thinking: The final model incorporates conditional statements ("if(t<0.8,0.965*2,0)") to represent the changing forces acting on the person. This exemplifies the integration of computational thinking into physics education, enabling students to represent complex physical phenomena using logical and mathematical operations.
Important Ideas/Facts:
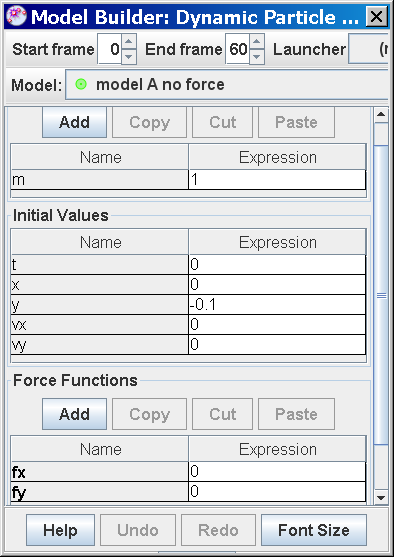
- Model A (No Force): When no force is applied (fx = 0), the model predicts no motion (vx = 0). This serves as a baseline and emphasizes the role of forces in initiating motion.
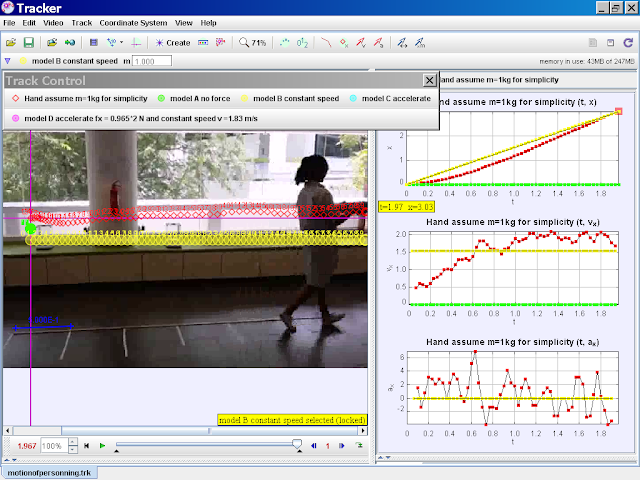
- Model B (Constant Speed): By introducing an initial velocity (vx = 1.54), the model demonstrates constant velocity motion when no net force is present. This reinforces Newton's first law of motion.
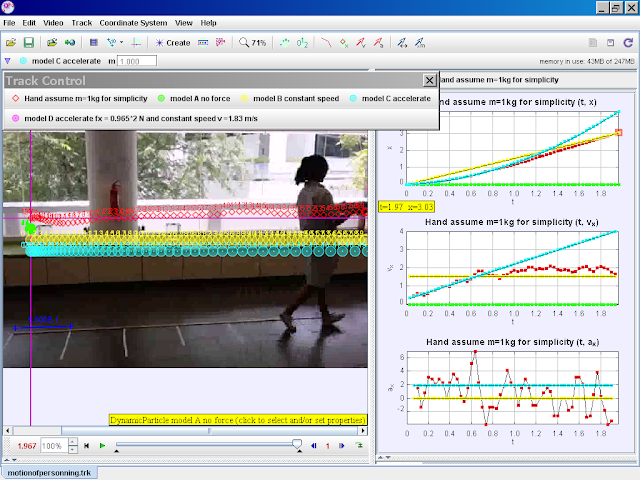
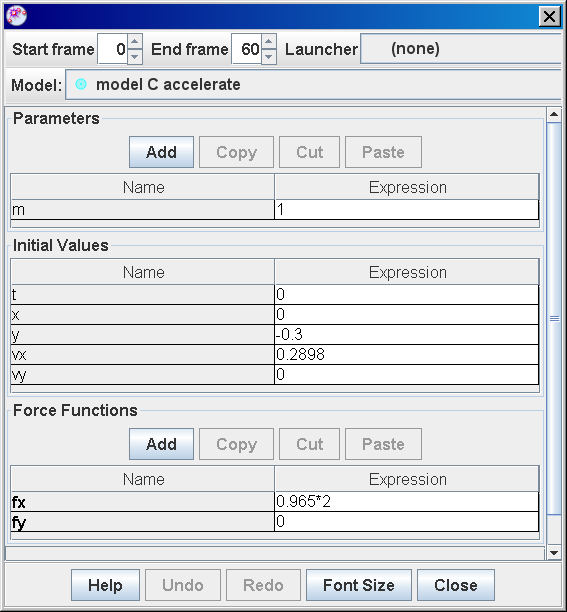
- Model C (Accelerate): A constant force (fx = 0.965*2 N) results in constant acceleration. This value is derived from the parabolic fit of the observed data, highlighting the link between experimental data and model parameters.
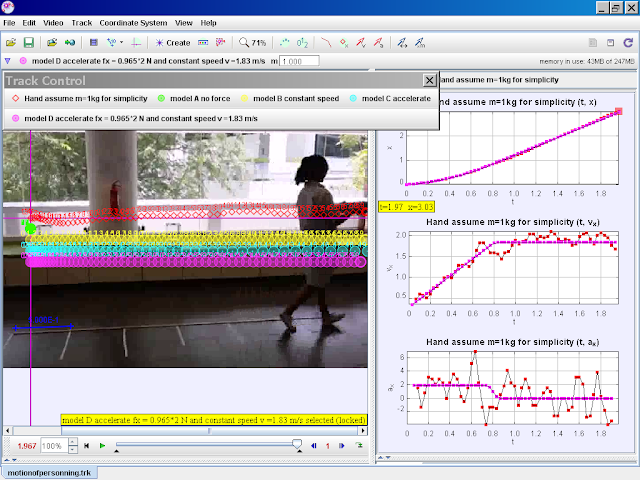
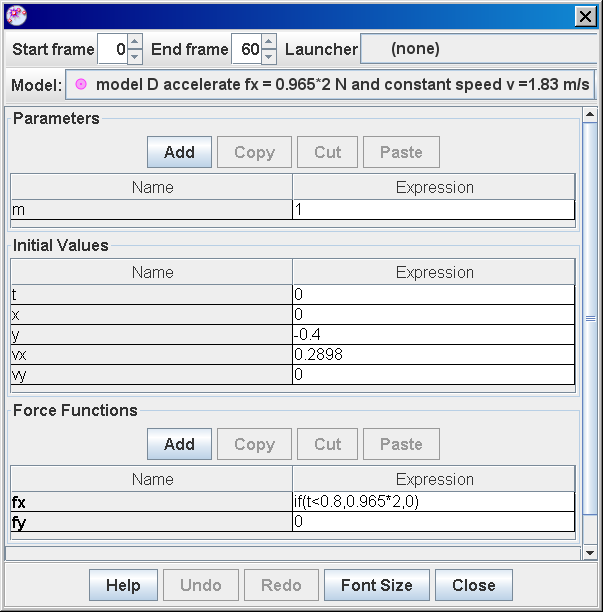
- Model D (Combined Acceleration and Constant Speed): This model incorporates both acceleration and constant velocity phases by introducing a time-dependent force. For t < 0.8 seconds, a force produces acceleration. After t = 0.8 seconds, the force becomes zero, resulting in constant velocity motion. This complex model provides a more accurate representation of the actual motion and demonstrates the interplay of Newton's first and second laws.
Key Quotes:
- "when fx = 0.965*2 (from data analysis trend line parabolic fit, coefficient of A which is ( \frac{1}{2}a )) and initial vx = 0.2898 (from data analysis tool of mass A hand) , there is constant acceleration motion." - Demonstrates how model parameters are derived from the analysis of the real-world data.
- "when fx = if(t<0.8,0.965*2,0) (computational thinking and mathematical demonstrating newton's 2nd and 1st law together)" - Highlights the use of computational thinking to model complex physical phenomena.
Conclusion: This Tracker-based pedagogy offers a hands-on, inquiry-driven approach to learning about motion and forces. By progressively building and refining models, students gain a deeper understanding of Newton's laws and develop skills in data analysis, visualization, and computational thinking.
Tracker Motion of Person: A Study Guide
Short-Answer Questions
- Describe Model A in the Tracker Motion of Person pedagogy and explain why there is no motion.
- Explain how Model B differs from Model A and what type of motion is observed in Model B.
- In Model C, how is the value of acceleration determined and what is the limitation of this model?
- Model D is considered the most accurate representation of the real motion. What features distinguish Model D from the previous models?
- What is the significance of the conditional statement "fx = if(t<0.8,0.965*2,0)" in Model D?
- How does the visualization in the Tracker models aid in understanding the motion of the person?
- What is the role of Newton's laws in the development of the Tracker Motion of Person models?
- Explain how data analysis tools within Tracker contribute to the model building process.
- What are the advantages of using a progressive model building approach in physics education?
- How does the Tracker software facilitate the exploration and understanding of motion concepts?
Answer Key
- Model A represents a scenario with no applied force (fx = 0). According to Newton's first law of motion, an object at rest stays at rest, and an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced force. Since there is no force, the velocity remains zero, and there is no motion.
- Model B introduces an initial velocity (vx = 1.54) while still maintaining zero net force (fx = 0). This results in constant velocity motion as per Newton's first law. The object moves at a constant speed in a straight line. Model B differs from Model A by incorporating initial velocity, leading to motion.
- In Model C, the acceleration is determined from the parabolic fit of the position-time data obtained from Tracker. The coefficient of the quadratic term (A) in the parabolic equation represents half the acceleration (A = 1/2a). The limitation of Model C is that it assumes constant acceleration throughout the motion, which might not perfectly represent the real motion.
- Model D incorporates both acceleration and constant velocity phases, making it a more realistic depiction of the actual motion. Unlike previous models, it utilizes a conditional statement to define the force, accounting for changing motion characteristics. It combines Newton's first and second laws to provide a comprehensive model.
- The conditional statement "fx = if(t<0.8,0.9652,0)" implies that a constant force (0.9652 N) acts on the object for the first 0.8 seconds, causing acceleration. After 0.8 seconds, the force becomes zero, resulting in constant velocity motion based on Newton's first law.
- The visualization in Tracker allows for a direct comparison between the model's predicted motion and the actual motion tracked from the video. This visual representation helps students identify discrepancies between the model and reality, facilitating the iterative model building process and enhancing understanding.
- Newton's laws of motion form the foundation for the Tracker Motion of Person models. The models reflect Newton's first law (inertia) in scenarios with zero net force and Newton's second law (F = ma) in cases with acceleration. The models demonstrate the application of these laws in real-world motion.
- Tracker's data analysis tools enable users to extract position-time data from the video, fit curves to the data, and determine parameters like velocity and acceleration. These tools are crucial for quantifying the motion, informing the model parameters, and evaluating the model's accuracy.
- A progressive model building approach encourages students to start with simple models and gradually refine them by incorporating additional factors and complexity. This iterative process fosters a deeper understanding of the underlying physics principles, promotes critical thinking, and highlights the role of assumptions in modeling.
- Tracker software enables students to analyze real-world videos, visualize motion, and build mathematical models to represent that motion. It bridges the gap between theoretical concepts and practical applications, making physics more tangible and engaging for learners.
Essay Questions
- Analyze the progression of the four models (A, B, C, and D) in the Tracker Motion of Person pedagogy. Discuss how each model builds upon the previous one, incorporating additional physics concepts and leading to a more accurate representation of the observed motion.
- Explain the role of Newton's laws of motion in the development and interpretation of the Tracker Motion of Person models. Provide specific examples from the models to illustrate the application of each law.
- Discuss the importance of data analysis in the Tracker Motion of Person activity. How do the data analysis tools within Tracker contribute to the model building process and the validation of the models?
- Critically evaluate the strengths and limitations of using Tracker software for teaching physics concepts. Discuss how Tracker can enhance student understanding of motion while considering potential drawbacks or challenges.
- Explain how the Tracker Motion of Person pedagogy exemplifies a progressive model building approach in physics education. Discuss the benefits of this approach for student learning and engagement in physics.
Glossary of Key Terms
- Tracker: Open-source video analysis and modeling software used for studying motion in physics.
- Progressive Model Building: A pedagogical approach where models are developed iteratively, starting with simple representations and gradually incorporating complexity to better reflect reality.
- Newton's First Law of Motion: Also known as the law of inertia, it states that an object at rest stays at rest, and an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced force.
- Newton's Second Law of Motion: This law describes the relationship between force, mass, and acceleration. It states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass (F = ma).
- Constant Velocity Motion: Motion where an object moves at a constant speed in a straight line, experiencing zero acceleration.
- Constant Acceleration Motion: Motion where an object experiences a constant change in velocity over time, resulting in a curved trajectory.
- Parabolic Fit: Fitting a parabolic curve to experimental data points, often used to model motion with constant acceleration.
- Conditional Statement: A statement in programming or mathematics that executes different actions based on whether a specific condition is true or false.
- Data Analysis Tools: Features within software like Tracker that allow users to analyze data, extract information, and derive parameters like velocity and acceleration.
- Visualization: The graphical representation of data or models, aiding in understanding and interpretation.
Video
https://youtu.be/ZFyy3LYPVIg tracker modeling explained by lookang lawrence wee
Tracker Motion of Person Progressive Model Building Pedagogy
model A no force
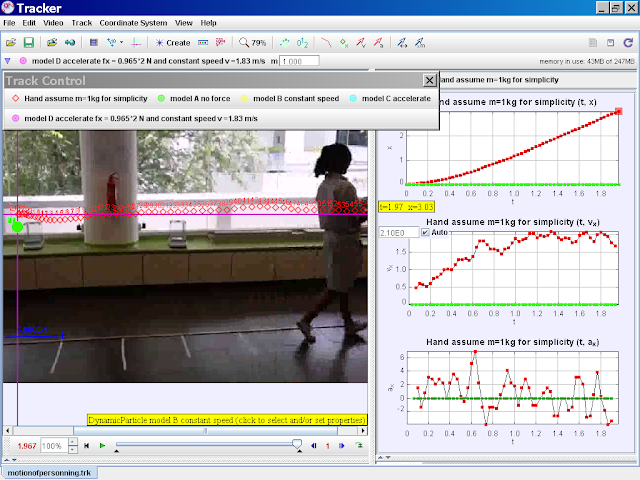 |
| http://weelookang.blogspot.sg/2015/06/tracker-motion-of-person-progressive.html TRZ Download, Download2 Video Download, Download2 author video: ning, model: lookang when fx = 0 , there is no motion, vx =0 |
 |
|
author video: ning, model: lookang when fx = 0 , there is no motion, vx =0, note that y = -0.1 is for visualization purposes. |
model B constant speed
 |
|
author video: ning, model: lookang when fx = 0 , there is no motion, vx =1.54, note that y = -0.2 is for visualization purposes |
model C accelerate
\( \frac{1}{2}a \)
 |
|
author video: ning, model: lookang when fx = 0.965*2 , and initial vx = 0.2898, there is constant acceleration motion,, note that y = -0.3 is for visualization purposes |
model D accelerate fx = 0.965*2 N for t = 0 to 0.8 s and constant speed v =1.83 m/s for t> 0.8 s
 |
|
author video: ning, model: lookang when fx = if(t<0.8,0.965*2,0) , and initial vx = 0.2898, there is constant acceleration motion,, note that y = -0.4 is for visualization purposes |
Tracker Motion of Person Progressive Model Building Pedagogy is made clear by lookang.
many thanks to the Open Source Physics community, +Douglas Brown and many more of them
Tracker Motion of Person: FAQ
1. What is the purpose of the "Tracker Motion of Person" project?
This project utilizes the Tracker software to analyze the motion of a person and progressively build mathematical models that represent the observed movement. It aims to demonstrate the application of physics principles, specifically Newton's laws of motion, to real-world scenarios.
2. How does the project use Tracker software?
Tracker is a video analysis tool that allows you to track the movement of objects in a video frame by frame. By marking the position of the person in each frame, Tracker generates data on their position, velocity, and acceleration over time. This data is then used to build and refine mathematical models.
3. What are the different models used in the project and how do they differ?
The project utilizes four progressive models:
- Model A (No Force): Assumes no net force acting on the person, resulting in no motion (vx = 0).
- Model B (Constant Speed): Assumes no net force and an initial velocity, leading to constant velocity motion.
- Model C (Accelerate): Introduces a constant force, calculated from data analysis, resulting in constant acceleration motion.
- Model D (Accelerate & Constant Speed): Combines acceleration and constant velocity by applying force for a specific time interval and then setting it to zero.
Each model builds upon the previous one, adding complexity and bringing the simulation closer to the actual motion observed in the video.
4. How is data analysis used to refine the models?
Tracker provides tools to analyze the motion data. Features like trend lines and parabolic fit help determine parameters like initial velocity and acceleration. These values are then used to define the forces and initial conditions in the models.
5. What is the significance of the expression fx = if(t<0.8,0.965*2,0) in Model D?
This expression utilizes conditional logic to simulate a more realistic scenario. For the first 0.8 seconds, a constant force (0.965*2 N) is applied, causing acceleration. After 0.8 seconds, the force becomes zero, resulting in constant velocity motion. This approach reflects how forces might act in real-world situations, leading to a more accurate representation of the person's movement.
6. How does this project demonstrate Newton's Laws of Motion?
The project showcases all three of Newton's Laws:
- First Law: Model A and the constant velocity phase in Model D illustrate an object at rest or in uniform motion staying that way unless acted upon by a net force.
- Second Law: Models C and D demonstrate how a net force produces acceleration proportional to the force and inversely proportional to the mass.
- Third Law: While not explicitly modeled, the act of walking itself involves action-reaction forces between the person's foot and the ground.
7. What are the limitations of the models developed in this project?
The models simplify real-world complexities. Factors like friction, air resistance, and variations in the applied force are not fully accounted for. As a result, while the models provide a good approximation, they may not perfectly match the nuances of the person's actual movement.
8. What are the educational benefits of this project?
The project provides a hands-on, inquiry-based approach to learning physics concepts. It helps students:
- Visualize and analyze motion: Understanding concepts like position, velocity, and acceleration in a tangible way.
- Apply Newton's Laws: Seeing how these fundamental laws govern real-world motion.
- Develop modeling skills: Learning how to build and refine mathematical models to represent physical phenomena.
- Engage in computational thinking: Using logic and conditional statements to create more dynamic simulations.
- Details
- Parent Category: 03 Motion & Forces
- Category: 02 Dynamics
- Hits: 17443