About

Topics

Measurement of length and time

Description

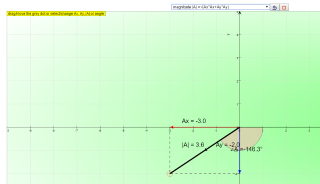
A vector is a quantity that has both magnitude and direction. Displacement, velocity, acceleration, and force are the vector quantities. in simpler examples, vectors were simply directed up, down, left or right. In situations in which vectors are directed at angles to the customary x(horizontal)-y(vertical) coordinate axes, a useful mathematical trick will be employed to transform the vector into two parts with each part being directed along the coordinate axes. For example, a vector that is directed northwest can be thought of as having two parts - a northward part and a westward part. A vector that is directed upward and rightward can be thought of as having two parts - an upward part and a rightward part.

Calculate the components of the vector A

1. click reset to generate a new random vector A of length |A| at an angle of theta to the positive x axis.
2. use the formula Ax = |A|cos(theta) to find the x direction component Ax.
3. use the formula Ay = |A|sin(theta) to find the y direction component Ay.
4. click reset to random generate a new vector A.
5. test yourself whether you have enough practice calculating Ax and Ay.

Other interesting fun activities

1. this model can be used to calculate any length |A| by keying in the values such as |A| =500 and theta = 63 degrees. Select the checkboxes Ax and Ay to see the new answers.
2. when Ax is selected, the PLAY button animates the effects of changing Ax alone.
3. when Ay is selected, the PLAY button animates the effects of changing Ay alone.
4. explore your own vector(s) here to test your understanding.
5. leave me a Google+ comment/question/requests etc here http://weelookang.blogspot.sg/2014/10/components-vector-model.html

Sample Learning Goals

(e) state what is meant by scalar and vector (how to resolve) quantities and give common examples of each

Version:

1. http://weelookang.blogspot.sg/2014/10/components-vector-model.html
2. 
   

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

http://iwant2study.org/lookangejss/01_measurement/ejss_model_horizontalvertical/horizontalvertical_Simulation.xhtml

Learning Objectives: https://sites.google.com/moe.edu.sg/a-level-physics-tlg/foundations-of-physics/quantities-measurement

Learning Outcomes: H2 - 1(h)(i)(j)

Curriculum Emphasis: Ways of Thinking and Doing [WOTD] https://vle.learning.moe.edu.sg/mrv/moe-library/lesson/view/c788167e-5865-4166-b147-89330b50b6b2/cover  SLS lesson includes questions that can be repeated indefinitely with random values inserted.

Topics

Measurement of length and time

Description

A vector is a quantity that has both magnitude and direction. Displacement, velocity, acceleration, and force are the vector quantities. in simpler examples, vectors were simply directed up, down, left or right. In situations in which vectors are directed at angles to the customary x(horizontal)-y(vertical) coordinate axes, a useful mathematical trick will be employed to transform the vector into two parts with each part being directed along the coordinate axes. For example, a vector that is directed northwest can be thought of as having two parts - a northward part and a westward part. A vector that is directed upward and rightward can be thought of as having two parts - an upward part and a rightward part.

Engage:

Vectors are fundamental in the physical sciences. They can be used to represent any quantity that has magnitude, has direction, and which adheres to the rules of vector addition. An example is velocity, the magnitude of which is speed. For example, the velocity 4 meters per second upward could be represented by the vector \( A_{y}\) = (0,4) (in 2 dimensions with the positive y axis as 'up'). Another quantity represented by a vector is force, since it has a magnitude and direction and follows the rules of vector addition. Vectors also describe many other physical quantities, such as linear displacement, displacement, linear acceleration, angular acceleration, linear momentum, and angular momentum. Other physical vectors, such as the electric and magnetic field, are represented as a system of vectors at each point of a physical space; that is, a vector field. Examples of quantities that have magnitude and direction but fail to follow the rules of vector addition: Angular displacement and electric current. Consequently, these are not vectors.

Component:

As explained above a vector is often described by a set of vector components that add up to form the given vector. Typically, these components are the projections of the vector on a set of mutually perpendicular reference axes (basis vectors). The vector is said to be decomposed or resolved with respect to that set. For simplicity, let's assume x and y direction as the reference axes, referring to the model above.

the equations for the components are:

 \( A_{x} = A cos( \theta) \)

 \( A_{y} = A sin( \theta) \)

 

Model:

This model uses the following equations:

Length or Magnitude |A|:

The length or magnitude or norm of the vector a is denoted by |A|.

 \( |A| = \sqrt {( A_{x}^{2}+A_{y}^{2})} \)

Angle:

The angle in radian of the vector that makes with the positive x axis is

\( \theta = tan^{-1} (\frac {A_{y}}{A_{x}}) \)

the conversion to degree is

\( \theta_{degree} = (tan^{-1} (\frac{A_{y}}{A_{x}}) )( \frac{180}{\pi}) \)

or

\( \theta_{degree} = ( \theta )( \frac{180}{\pi}) \)

in the design of the slider values which shows in degree, the equation that converts back from degree to radian is used

\( \theta = ( \theta_{degree} )( \frac{\pi}{180}) \)

Calculate the components of the vector A

1. click reset to generate a new random vector A of length |A| at an angle of theta to the positive x axis.
2. use the formula Ax = |A|cos(theta) to find the x direction component Ax.
3. use the formula Ay = |A|sin(theta) to find the y direction component Ay.
4. click reset to random generate a new vector A.
5. test yourself whether you have enough practice calculating Ax and Ay.

Other interesting fun activities

1. this model can be used to calculate any length |A| by keying in the values such as |A| =500 and theta = 63 degrees. Select the checkboxes Ax and Ay to see the new answers. 
2. when Ax is selected, the PLAY button animates the effects of changing Ax alone.
3. when Ay is selected, the PLAY button animates the effects of changing Ay alone.
4. explore your own vector(s) here to test your understanding.
5. leave me a Google+ comment/question/requests etc herehttp://weelookang.blogspot.sg/2014/10/components-vector-model.html 

Sample Learning Goals

(e) state what is meant by scalar and vector(how to resolve) quantities and give common examples of each

 

Version:

1. http://weelookang.blogspot.sg/2014/10/components-vector-model.html

2. http://weelookang.blogspot.sg/2014/10/components-vector-model.html CLICK https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_horizontalvertical/horizontalvertical_Simulation.xhtml author: lookang, Fu-Kwun, Andreu Glasmann, Wolfgang Christian, and Mario Belloni offline use: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_horizontalvertical.zip source: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_src_horizontalvertical.zip author of EJS 5: Paco.

3. http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=662.0 Represent a vector as horizontal and vertical components applet by Loo Kang Wee and Fu-Kwun Hwang
4. http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=661.0 Magnitude of a Vector by Loo Kang Wee and Fu-Kwun Hwang

 

Other Resources

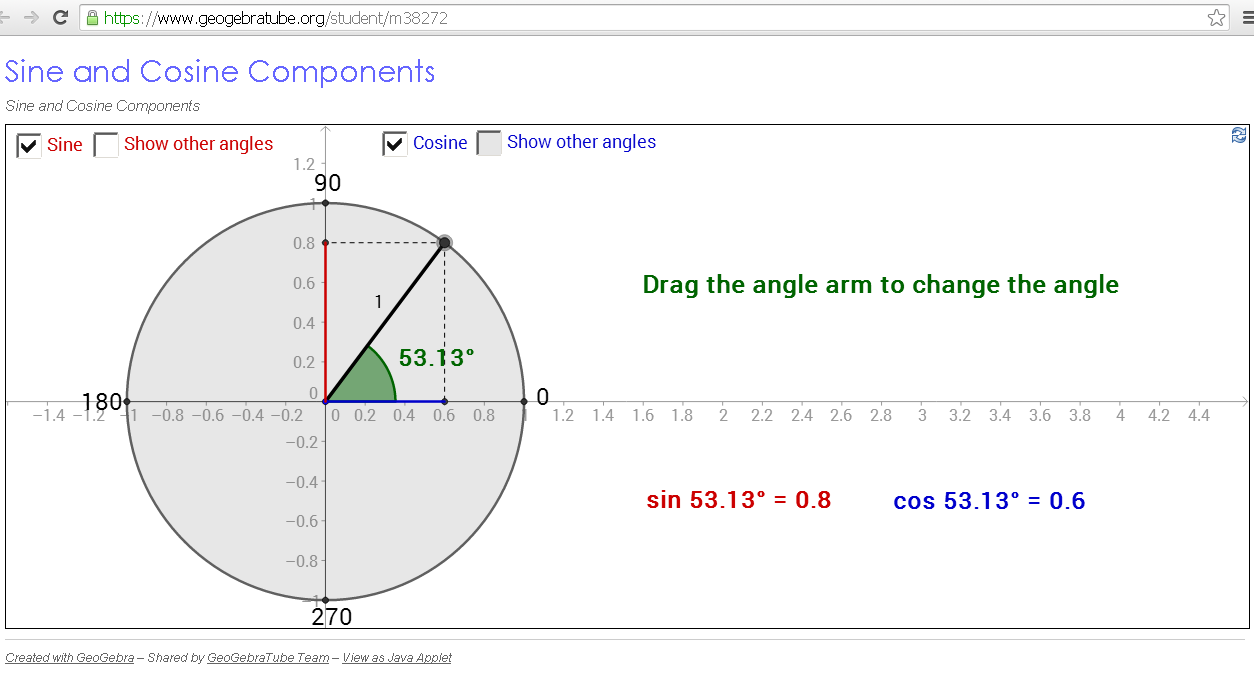
1. Example JavaScript Model Ill 3.1: Vector Decomposition written by Andreu Glasmann, Wolfgang Christian, and Mario Belloni 
2. https://www.geogebratube.org/student/m38272 

end faq

{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}