About

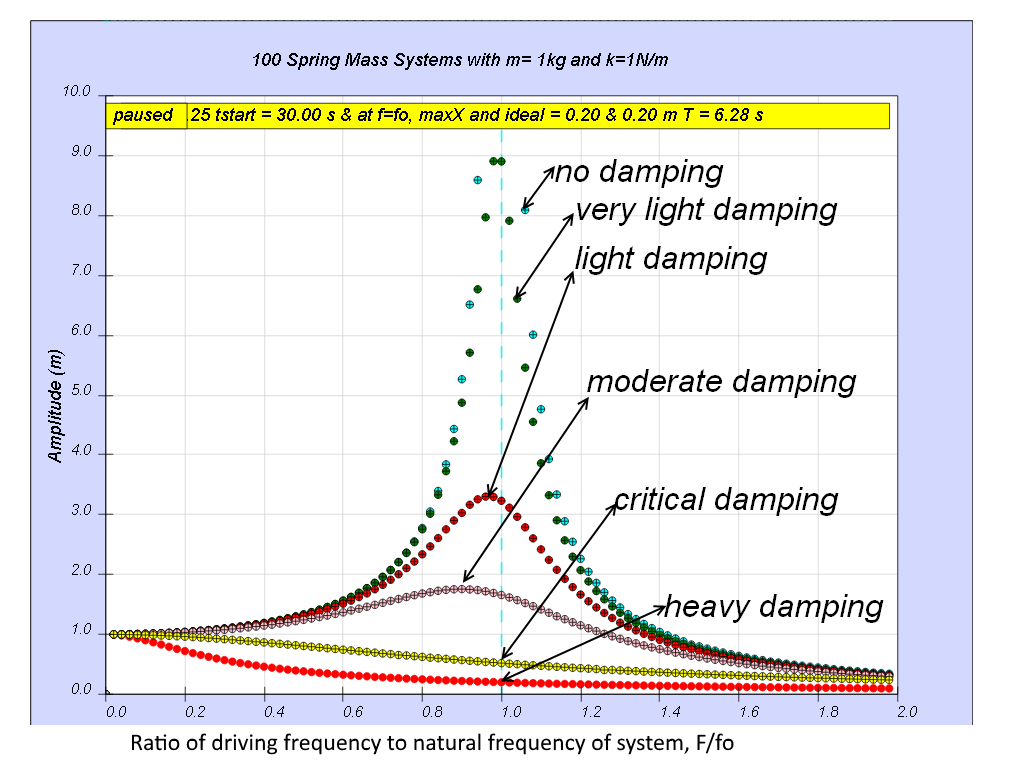
1.7.4 The response of the oscillatory system depends on the value of the frequency of the periodic force (also known as the driving frequency).                LO (k)

When the driving frequency f  is close to or equal to the natural frequency f_o of the oscillating system, maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude.  This phenomenon is called resonance.      

 A more accurate and complicated picture could be found on Wikipedia.

 

This computer model can be used to generate a similar data representation when using the instruction found on the html below the model.

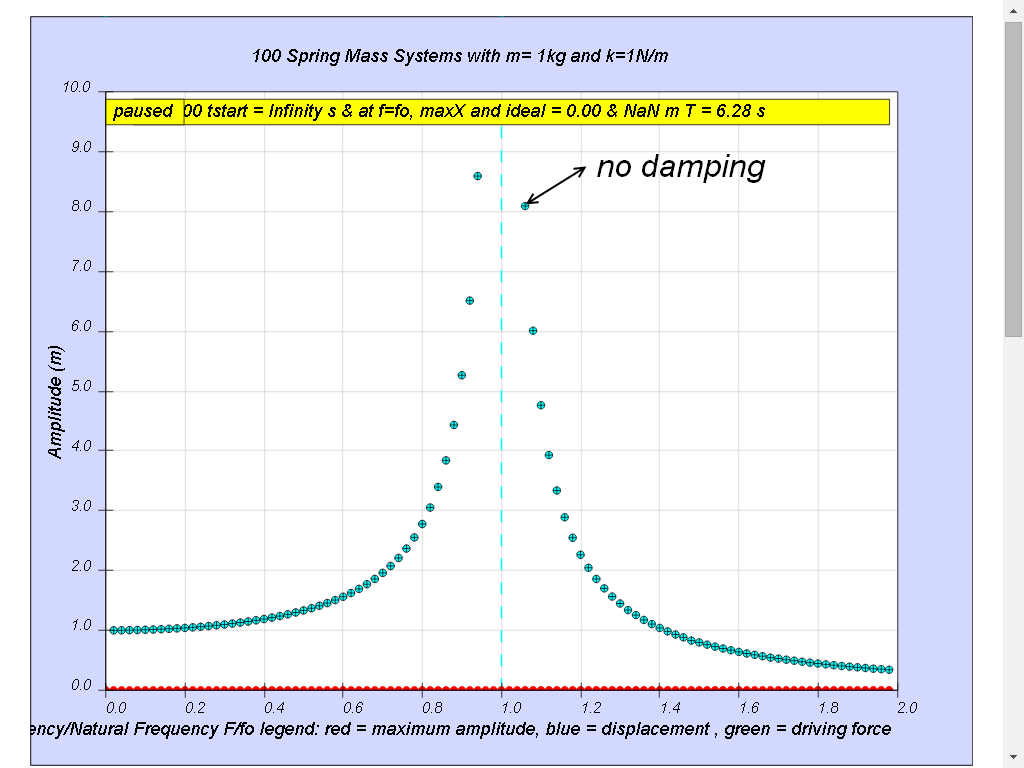
1.7.4.1 Case 1: b=0 no damping.

All 100 spring mass systems oscillates forever without coming to rest. Notice when the ratio of driving frequency to natural frequency f_o of the oscillating system  f/fo = 1  maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude (extended beyond 10).  This phenomenon is called resonance. 

  

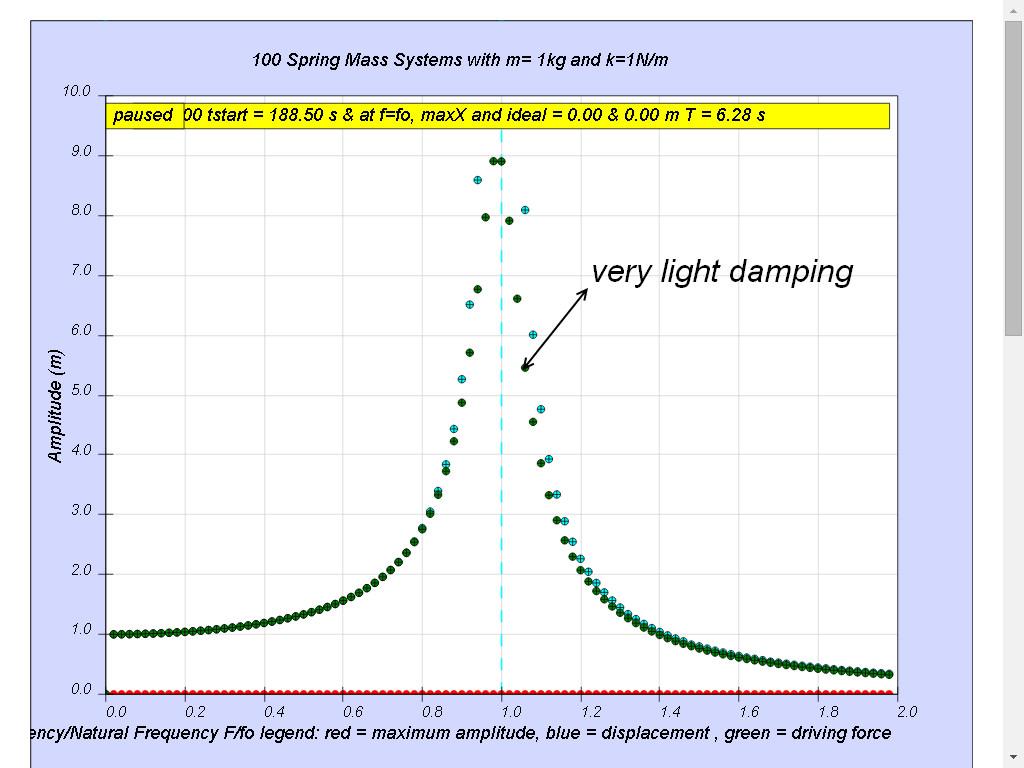
1.7.4.2 Case 2: b=0.1 very light damping

Notice when the ratio of driving frequency to natural frequency f_o of the oscillating system  f/fo = 1  maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude (equal 10 m).  This phenomenon is called resonance. 

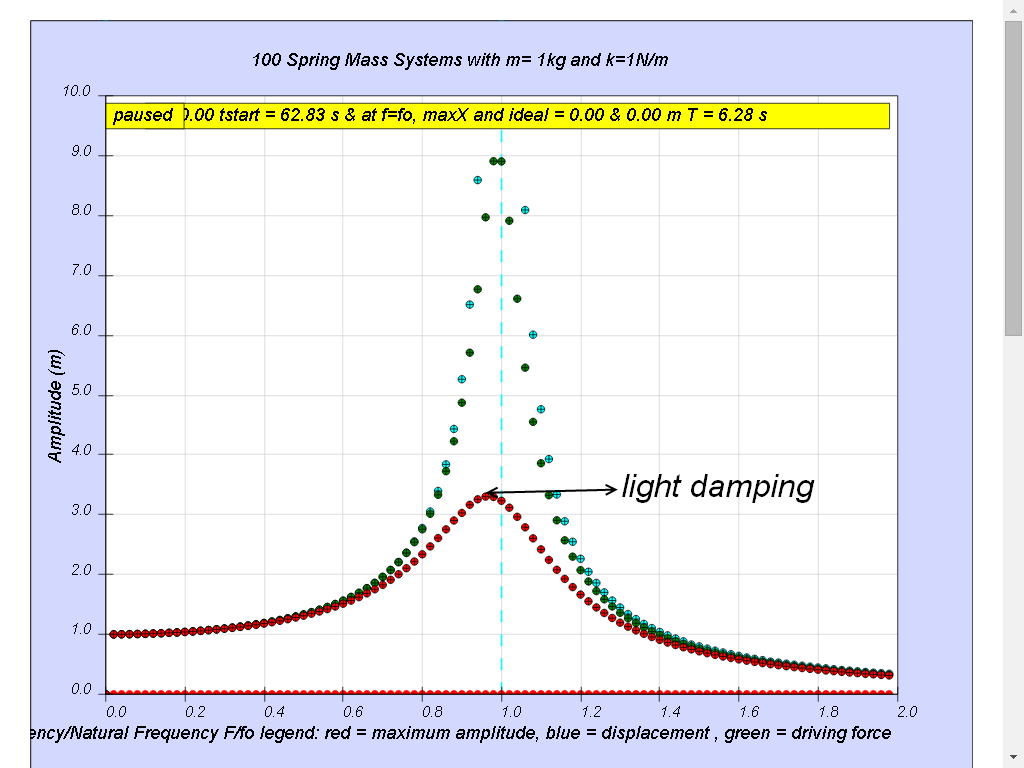
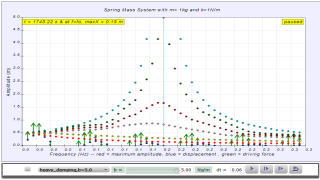
1.7.4.3 Case3: b=0.3 light damping

Notice when the ratio of driving frequency to natural frequency f_o of the oscillating system  f/fo slightly less than 1,  maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude (about 3.3).  This phenomenon is called resonance. 

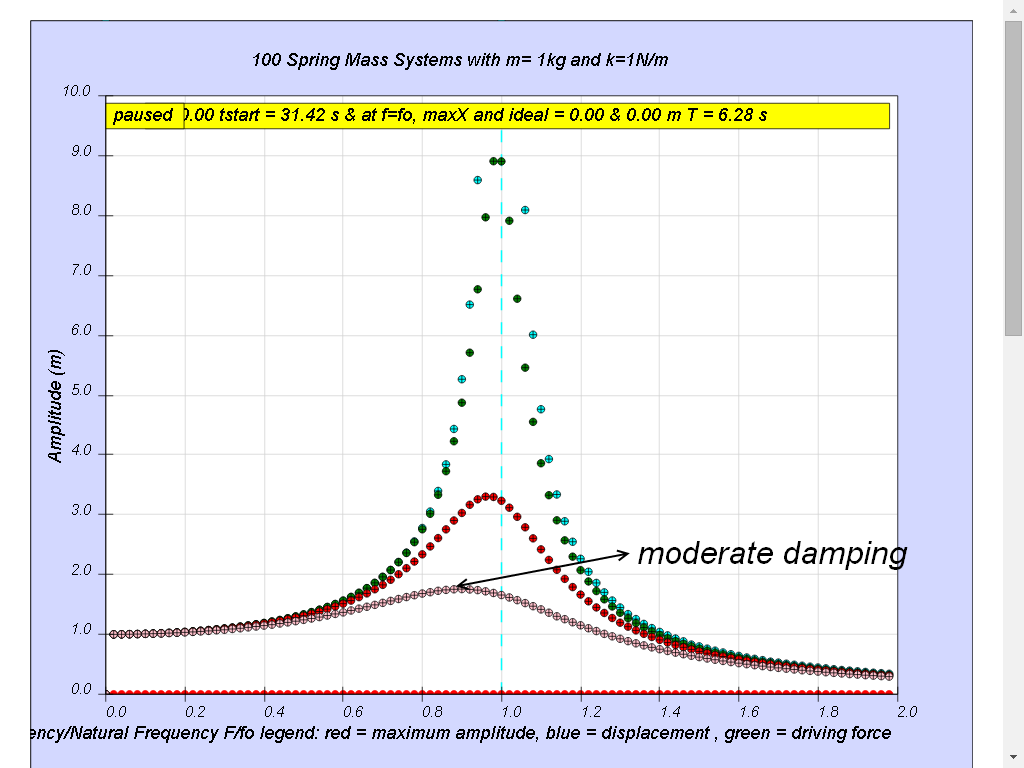
1.7.4.4 Case4: b =0.6 moderate damping

Notice when the ratio of driving frequency to natural frequency f_o of the oscillating system  f/fo slightly less than 1 about 0.9 in this case,  maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude (about 1.8).  This phenomenon is called resonance.

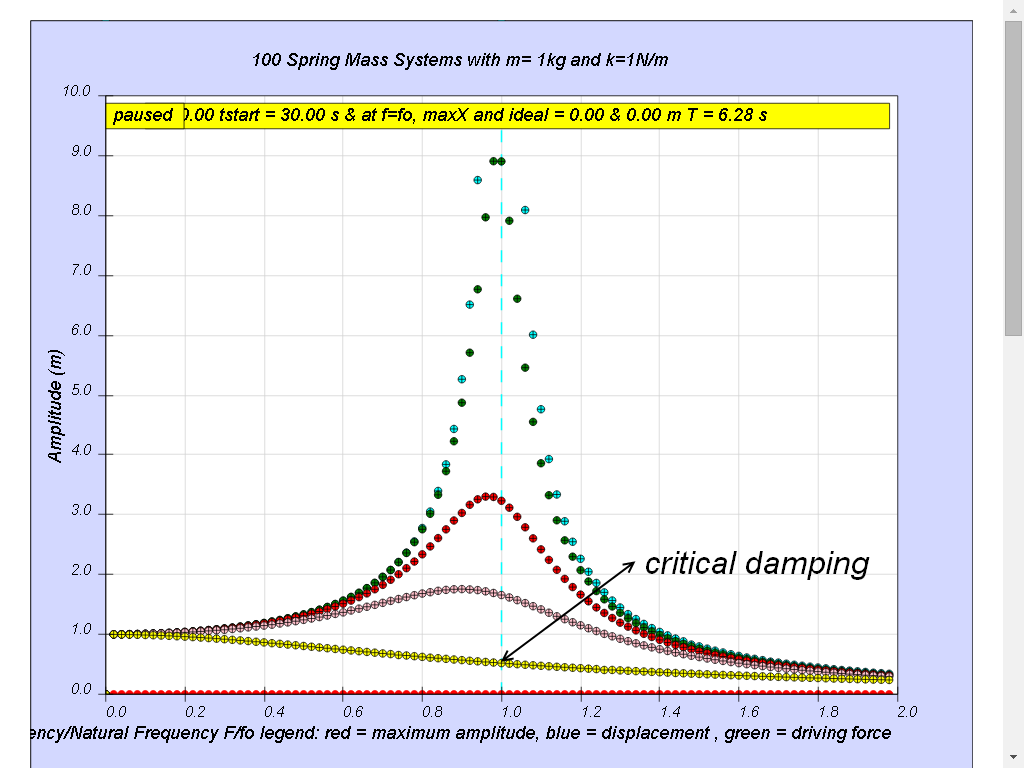
1.7.4.5 Case5: b = 2.0 critical damping

Notice the resonance does not occur anymore. 

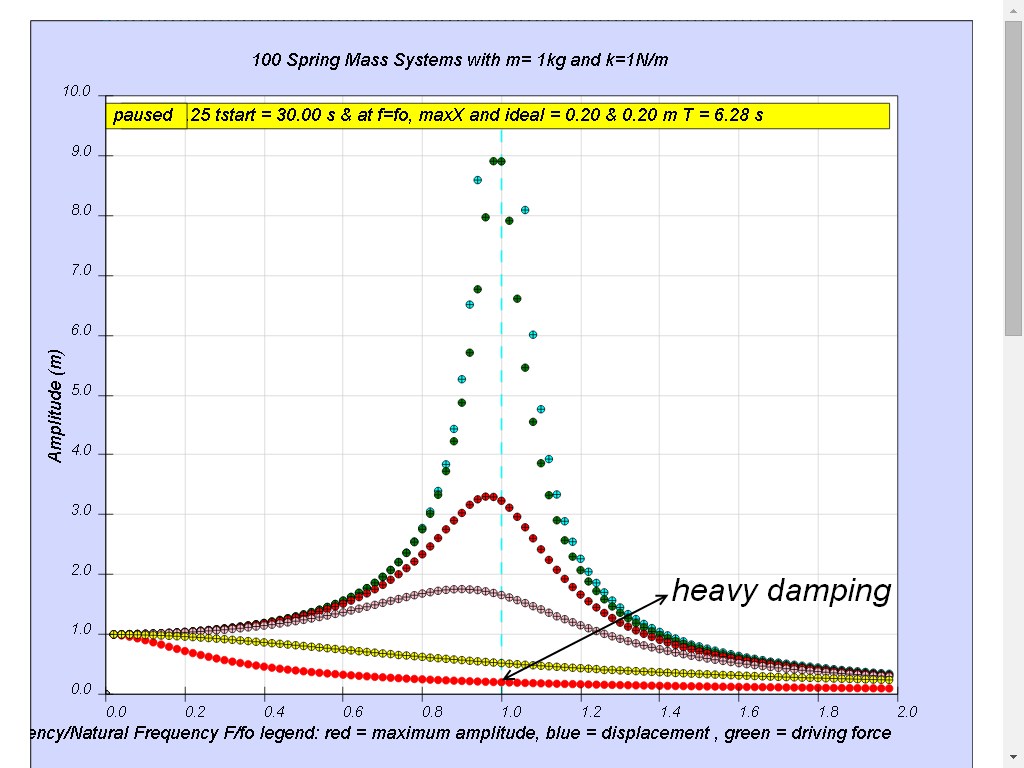
1.7.4.6 Case6: very heavy damping

Notice the resonance does not occur anymore. 

1.7.5 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/88

1.7.6 YouTube explanation:

http://youtu.be/tl4hfZ3TR6U

1.7.7 YouTube

http://youtu.be/LV_UuzEznHs  How is this video related to resonance? Hint: consider the shaking support table is the driver, moving an driver frequency f, and the natural frequency of the left, middle and right structure each have their own natural frequency f₀₁, f₀₂, f₀₃.

http://youtu.be/17tqXgvCN0E This video shows the oscillating of a wine glass by playing sound (driver) at its(wine glass) natural frequency resulting in resonance.Note stroboscope is used to observe the resonant effect better.

http://youtu.be/M8ztJGT6AHc Marina Bay Sands cantilever - real world application of resonance.
Note that video ends at 5.40 min.

http://youtu.be/1yaqUI4b974 Though not really in A-Level Physics syllabus, the experiment shows the beauty of physics where sound at certain frequencies can produce detailed 2 dimensions patterns of sands that tends to be deposited at positions where the displacement is zero and areas of resonances (high amplitudes) the sand tend to be disturbed and move away from these position, resulting in the detailed patterns of sands.

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.; leetatleong

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM24/SHM24_Simulation.xhtml

Briefing Document: ⚛️Resonance in Oscillatory Systems

Subject: Analysis of "10.7.4 The response of the oscillatory system depends on the value of the frequency of the periodic force HTML5 Applet Simulation Model"

Source: Open Educational Resources / Open Source Physics @ Singapore

Date: October 26, 2024

Overview

This document provides a review of an interactive simulation model focused on the phenomenon of resonance in oscillating systems. The model, titled "10.7.4 The response of the oscillatory system depends on the value of the frequency of the periodic force," is an HTML5 applet designed to illustrate how the frequency of a driving force impacts the amplitude of an oscillating system. The core concept explored is resonance, which occurs when the driving frequency matches or is near the system's natural frequency, leading to maximum energy transfer and large-amplitude oscillations.

Key Themes and Ideas

1. Resonance:

• The primary focus is on understanding resonance. The source states: "When the driving frequency f is close to or equal to the natural frequency fo of the oscillating system, maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude. This phenomenon is called resonance."
• Resonance is presented as a key concept in understanding how external forces influence oscillating systems.
• The model provides an interactive way to demonstrate this principle.

1. Driving Frequency vs. Natural Frequency:

• The simulation emphasizes the relationship between the driving frequency (f) of an external periodic force and the natural frequency (f0) of the oscillating system.
• Maximum energy transfer and the largest amplitude of oscillation occur when f is near or equal to f0, specifically when the ratio f/f0 is close to or equals 1.

1. Damping Effects:

• The model demonstrates how damping affects the system's response to the driving force and the resonance phenomenon. Different cases with varying damping coefficients (b) are presented.
• No Damping (b=0): "All 100 spring mass systems oscillates forever without coming to rest...Notice when the ratio of driving frequency to natural frequency fo of the oscillating system f/fo = 1 maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude (extended beyond 10)." Here, resonance is very pronounced, with very high amplitudes.
• Very Light Damping (b=0.1): "Notice when the ratio of driving frequency to natural frequency fo of the oscillating system f/fo = 1 maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude (equal 10 m). This phenomenon is called resonance." The amplitude is still high but more contained than with no damping.
• Light Damping (b=0.3): "Notice when the ratio of driving frequency to natural frequency fo of the oscillating system f/fo slightly less than 1, maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude (about 3.3). This phenomenon is called resonance." Peak resonance occurs slightly below f/f0 = 1 and maximum amplitude is lower.
• Moderate Damping (b=0.6): "Notice when the ratio of driving frequency to natural frequency fo of the oscillating system f/fo slightly less than 1 about 0.9 in this case, maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude (about 1.8)." Peak resonance shifts further below f/f0 = 1 and maximum amplitude further decreases.
• Critical Damping (b=2.0) and Very Heavy Damping: "Notice the resonance does not occur anymore." Beyond a certain level, damping prevents resonance from occurring at all.

1. Simulation Model:

• The HTML5 applet allows users to interact with a model of an oscillatory system.
• It includes adjustable parameters, likely allowing users to modify the driving frequency and damping to observe their effects in real-time.
• The simulation's goal is to enable users to visually experience resonance.

1. Real-World Examples

• The resource includes links to YouTube videos demonstrating real-world examples of resonance:
• One video shows the shaking of a support table (acting as a driver) causing different structures to oscillate at different amplitudes depending on how close the driving frequency is to their natural frequencies.
• Another video illustrates a wine glass oscillating and breaking due to sound waves (driver) at the glass's natural frequency.
• There is mention of Marina Bay Sands cantilever, highlighting resonance in large structures.
• A final video illustrates patterns formed in sand due to resonance from specific sound frequencies.

Important Facts and Quotes

• Definition of Resonance: "When the driving frequency f is close to or equal to the natural frequency fo of the oscillating system, maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude. This phenomenon is called resonance."
• Ratio f/f0: The driving frequency and the natural frequency are closely related in achieving resonance. The maximum amplitude of oscillation occurs when this ratio is near or at 1, and it also depends on damping.
• Impact of Damping: Increased damping reduces the maximum amplitude of oscillation and can eventually prevent resonance.

Educational Value

This resource appears designed for educational purposes, particularly for students at the Junior College level. It offers:

• Visual Learning: The interactive applet facilitates a clear, visual understanding of resonance.
• Hands-on Experience: Users can manipulate the simulation to explore different scenarios.
• Real-World Connections: The inclusion of real-world examples helps connect abstract physics concepts to tangible phenomena.
• Accessibility: The HTML5 format makes it accessible on various devices including computers, tablets, and smartphones.
• Integration with other Resources: The model appears to be part of a larger collection of interactive physics simulations at the "Open Educational Resources / Open Source Physics @ Singapore" site.

Conclusion

The "10.7.4" simulation model provides a clear, interactive, and accessible platform for learning about resonance in oscillating systems. By varying the driving frequency and observing the effects of different levels of damping, users can gain an intuitive understanding of a key physics concept. The inclusion of real-world examples and links to further resources enhances the educational value.

Resonance in Oscillatory Systems: A Study Guide

Quiz

Instructions: Answer each question in 2-3 sentences.

1. What is the driving frequency in the context of an oscillatory system?
2. What is the natural frequency of an oscillating system?
3. What is resonance, and under what conditions does it occur?
4. What happens to the energy transfer when the driving frequency equals the natural frequency?
5. How does damping affect the amplitude of oscillations during resonance?
6. According to the text, how does very light damping affect the maximum amplitude of the oscillating system?
7. According to the text, how does light damping affect the ratio of driving to natural frequency when maximum amplitude is achieved?
8. What effect does moderate damping have on the ratio of driving to natural frequency when maximum amplitude is achieved?
9. What happens to the resonance phenomenon under critical damping?
10. What real-world example is given that is an application of resonance?

Quiz Answer Key

1. The driving frequency is the frequency at which an external periodic force is applied to an oscillatory system, causing it to oscillate. This force acts as the driver, pushing the system into motion at a specific rate.
2. The natural frequency is the inherent frequency at which an oscillating system will vibrate when disturbed, without an external force. It's determined by the system's physical properties, such as mass and stiffness.
3. Resonance is the phenomenon where an oscillating system vibrates with maximum amplitude when the driving frequency is close to or equal to its natural frequency. This occurs because energy is efficiently transferred from the driver to the system.
4. When the driving frequency equals the natural frequency, maximum energy is transferred from the driving force to the oscillatory system. This results in the system vibrating with a maximum amplitude, which is characteristic of resonance.
5. Damping reduces the amplitude of oscillations, especially at resonance. It dissipates energy from the system, meaning that the maximum amplitude achieved during resonance is lower than it would be with no damping.
6. According to the text, when the damping is very light, the maximum amplitude of the oscillating system will equal 10 meters when the ratio of driving frequency to natural frequency is equal to 1.
7. According to the text, when light damping is introduced the ratio of driving to natural frequency at which maximum amplitude is achieved is slightly less than one.
8. According to the text, moderate damping results in the maximum amplitude being achieved when the ratio of driving to natural frequency is about 0.9, slightly less than 1.
9. Under critical damping, the resonance phenomenon no longer occurs. The system will not achieve maximum amplitude regardless of the driving frequency.
10. The Marina Bay Sands cantilever is given as a real world application of resonance.

Essay Questions

Instructions: Answer each question in a well-structured essay format. These are not meant to be quick-answer questions.

1. Analyze the relationship between driving frequency and natural frequency in an oscillatory system. Discuss how their interaction leads to the phenomenon of resonance, and explain how this interaction is affected by different levels of damping.
2. Using specific examples from the provided text, explain how the level of damping influences the amplitude of the oscillations during resonance. Discuss how the amount of damping affects the sharpness of the resonance peak.
3. Discuss the practical implications of resonance in engineering and other fields, using examples from the provided source material and your own knowledge. Consider both the beneficial and detrimental aspects of resonance.
4. Compare and contrast the different cases of damping, from no damping to very heavy damping, on an oscillating system. Explain the role that damping plays in the transfer and dissipation of energy within the system, as described in the source text.
5. Critically evaluate the use of the provided HTML5 applet simulation models as tools for understanding the concepts of driving frequency, natural frequency, and resonance. How effective are these models in demonstrating these complex phenomena?

Glossary of Key Terms

• Oscillatory System: A system that exhibits periodic motion, such as a spring-mass system, pendulum, or any other system that moves back and forth.
• Driving Frequency (f): The frequency at which an external periodic force is applied to an oscillatory system. This force causes the system to oscillate or vibrate.
• Natural Frequency (f₀): The inherent frequency at which an oscillatory system will vibrate when disturbed and allowed to move freely. This frequency is determined by the physical properties of the system, such as its mass and stiffness.
• Resonance: A phenomenon that occurs when the driving frequency of an external force is close to or equal to the natural frequency of an oscillatory system, resulting in a maximum transfer of energy to the system, and causing it to vibrate with maximum amplitude.
• Damping: A process that dissipates energy from an oscillating system, causing the amplitude of its oscillations to decrease over time. Damping is often due to resistive forces like friction or air resistance.
• Amplitude: The maximum displacement or distance moved by an object from its equilibrium position during oscillation or vibration.
• Critical Damping: A specific level of damping where the system returns to its equilibrium position as quickly as possible without oscillating. At critical damping the maximum amplitude of the system during resonance cannot occur.

 Apps

https://play.google.com/store/apps/details?id=com.ionicframework.shm24app916792&hl=en

iCTLT e-poster video 2 minutes

1. Version 30 March 2016 Minister
2. Version 17 March 2016   
3. Version 14 March 2016 
4. Version February  

iCTLT e-poster presentation

   https://docs.google.com/a/moe.gov.sg/presentation/d/10ejVJIyXA8u2DILcEbJ-RACLxoPvvqrTiC02fqfNJIc/edit?usp=sharing

 https://docs.google.com/presentation/d/1g7U7dwjxdQ8k9Z62AzXEQCM3K0NcNqvxCXugOXv-qpA/edit#slide=id.p4

 https://docs.google.com/presentation/d/1lSySjVaEDlIRBniKie2xyCu3B6go2AjJqe00D_vUr5Q/edit#slide=id.g10abfba361_0_25

 

Frequently Asked Questions on Resonance and Oscillations

1. What is resonance in the context of oscillating systems? Resonance is a phenomenon that occurs when a periodic force (the driver) is applied to an oscillating system at a frequency that is close to or equal to the system's natural frequency. When this happens, maximum energy is transferred from the driver to the oscillating system, causing the system to vibrate with a large amplitude. This means the system's response to the driving force is greatly amplified.
2. How does the driving frequency relate to the natural frequency in resonance? Resonance occurs most effectively when the driving frequency (the frequency of the applied force) is close to or the same as the natural frequency of the oscillating system. The closer the driving frequency is to the natural frequency, the larger the amplitude of the oscillations will become. When these frequencies are exactly equal, the amplitude is at its theoretical maximum.
3. What is the role of damping in resonance? Damping is a force that opposes motion, gradually reducing the amplitude of oscillations over time. In the context of resonance, damping can significantly affect the amplitude of the system's response. Light damping allows resonance to occur with a large amplitude. As damping increases, the amplitude at resonance decreases. With critical or very heavy damping, resonance no longer occurs.
4. How does damping affect the ratio of driving frequency to natural frequency at which resonance occurs? With no damping or very light damping, resonance occurs when the ratio of driving frequency to natural frequency (f/f₀) is equal to 1. However, with light to moderate damping, the maximum amplitude may occur when the driving frequency is slightly less than the natural frequency (f/f₀ is slightly less than 1). As the damping increases, the resonance peak becomes less pronounced, and in the case of critical or very heavy damping, resonance does not occur.
5. What are some real-world examples of resonance? The provided sources mention a few real-world examples: the oscillating of a wine glass when sound is played at its natural frequency, causing it to vibrate and potentially shatter; the shaking support table in a video, representing a driver with a certain frequency that could affect the different structure natural frequency; and the Marina Bay Sands cantilever which needs to take into consideration resonance to avoid structural issues due to wind or other external forces.
6. How does the concept of resonance relate to the provided simulations and interactive models? The simulations allow users to manipulate parameters like driving frequency, damping, and natural frequency, observing the effects on the amplitude of oscillations. They provide a visual and interactive way to understand resonance and how these parameters influence it. For instance, the spring mass system simulations show how changing the driving frequency in relation to the natural frequency and also changing the damping affects the system, showcasing the concept of resonance clearly.
7. What is the significance of these types of interactive physics models in education? These interactive models allow students to explore abstract concepts like resonance in a visual, engaging way. By manipulating parameters and observing results, students can build a deeper understanding of the underlying principles of physics. These simulations allow students to learn at their own pace, in their own ways, and have an active role in learning rather than just being a passive receiver.
8. Besides resonance, what other physics concepts are explored in these resources? While the primary focus is on resonance and oscillations, the provided resources include a broad range of physics topics. These include Newtonian mechanics, simple harmonic motion, projectile motion, energy, work, power, gravitational fields, and even some elements of electromagnetism and optics. Many of these resources also involve other areas of STEM learning like trigonometry and other mathematical concepts, engineering and design. These diverse models offer interactive ways to learn across a wide range of physics topics.