About
1.2.10 Example
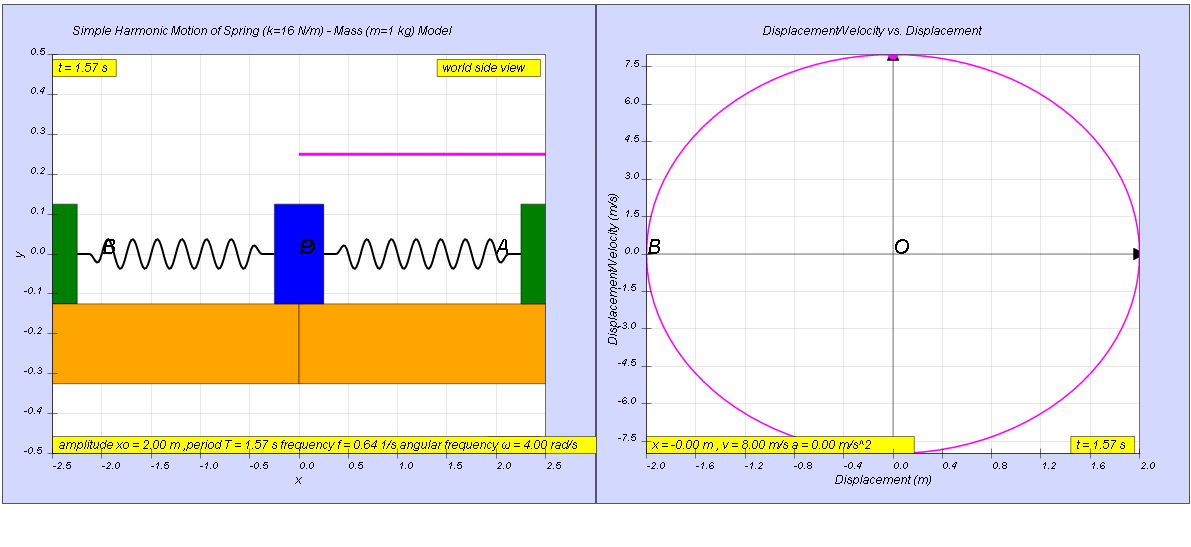
The graph of velocity against displacement of a body is shown below.
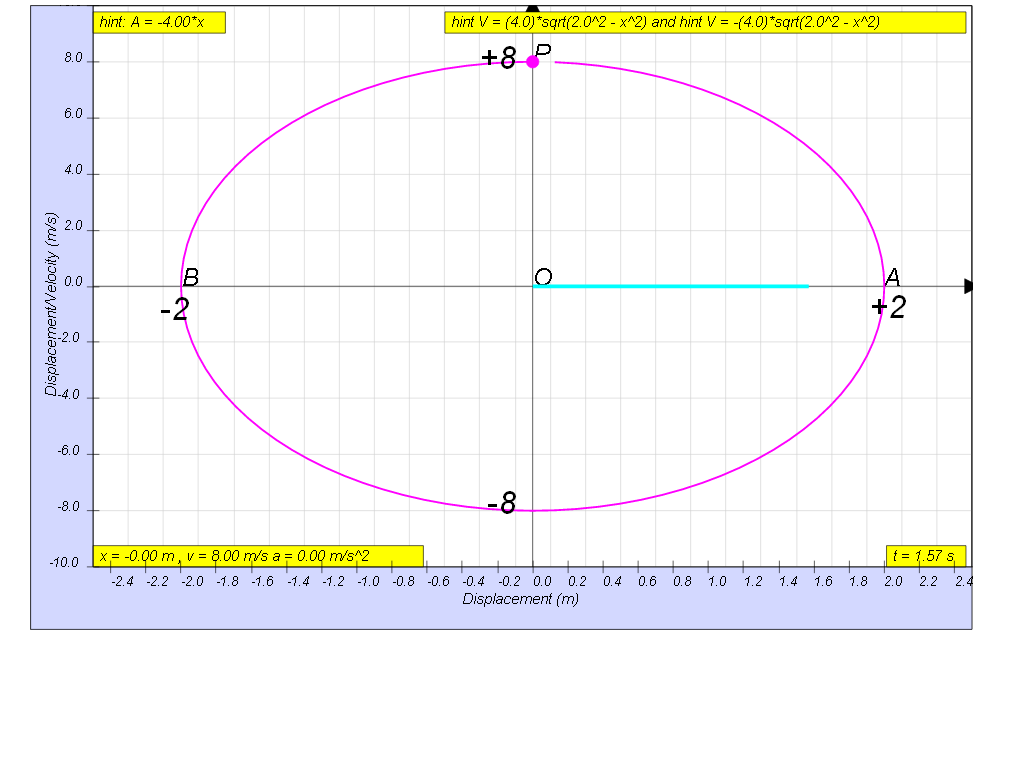
a) Explain why there are two values of velocity for zero displacement.
b) Explain why there are two values of displacement for zero velocity.
c) Using the maximum value of the velocity, determine the period of oscillation.
[when x =0, v =8(moving right) or -8(moving left),when v =0 , x = -2(at left) or 2(at right),1.6]
Hint:
1.2.10.1 Suggested Solution:
a) An oscillating body moves through the equilibrium position (zero displacement) alternately
in opposite directions.
b) An oscillating body has zero velocity when its displacement is maximum which occurs at the maximum amplitude positions. Hence, there are 2 values of displacement.
c) vo = xo ω
(8.0) = (2.0) ω
ω = 4.0 rad/s
thus
T = 1.57 s = 1.6 s (to 2 s.f.)
1.2.10.2 Model:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits
 This email address is being protected from spambots. You need JavaScript enabled to view it.
This email address is being protected from spambots. You need JavaScript enabled to view it.
Briefing Document: ⚛️Spring-Mass Oscillation Simulation
1. Introduction
This document provides an overview of the provided source, which details a JavaScript HTML5 applet simulation model of a spring-mass system undergoing simple harmonic motion (SHM). The source is part of the "Open Educational Resources / Open Source Physics @ Singapore" initiative. The focus of this specific simulation (SHM16) is on the relationship between velocity and displacement in SHM and understanding the period of oscillation.
2. Main Themes and Concepts
- Simple Harmonic Motion (SHM): The core concept is SHM, a type of periodic motion where the restoring force is proportional to the displacement. The simulation visualizes this in the context of a spring-mass system.
- Velocity vs. Displacement Relationship: A key aspect of this simulation is the graph of velocity versus displacement, which is an ellipse. The source emphasizes understanding why certain characteristics of this graph occur.
- Equilibrium Position: The simulation underscores the importance of the equilibrium position (zero displacement) and how the oscillating mass passes through it in opposite directions, resulting in two different velocity values when x=0.
- Maximum Amplitude: Similarly, the simulation helps visualize that the velocity is zero at the maximum amplitude positions, which results in two different x values when v=0.
- Period of Oscillation: The simulation provides data points to determine the period of oscillation using the maximum velocity and maximum displacement. The connection between the angular frequency, maximum velocity, and maximum displacement is highlighted.
- Interactive Learning: The simulation is designed as an interactive learning tool with a "Run Sim" button, designed for web browsers on various devices including desktops, laptops, tablets, and smartphones.
3. Key Ideas and Facts
- Simulation Parameters: The specific example uses a spring constant (k) of 16 N/m and a mass (m) of 1 kg.
- Velocity and Displacement Values:When displacement (x) is 0, the velocity (v) is either +8 m/s (moving right) or -8 m/s (moving left).
- When velocity (v) is 0, the displacement (x) is either -2 m (at the left-most position) or 2 m (at the right-most position). This indicates an amplitude of 2 meters.
- Angular Frequency (ω): The simulation calculates the angular frequency as 4.0 rad/s, based on the provided data points.
- Period of Oscillation (T): The calculated period of oscillation is 1.57 seconds which is approximately 1.6 s (to 2 significant figures). This is derived from the angular frequency using the formula T = 2π/ω.
- Educational Platform: The simulation is part of a larger collection of open-source educational physics resources, aiming to enhance physics education.
- Accessibility: The tool is designed for various platforms, making it easy for learners with various devices to access the resources.
4. Quotes from the Source
- Explanation for two velocity values at zero displacement: "An oscillating body moves through the equilibrium position (zero displacement) alternately in opposite directions."
- Explanation for two displacement values at zero velocity: "An oscillating body has zero velocity when its displacement is maximum which occurs at the maximum amplitude positions. Hence, there are 2 values of displacement."
- Calculation of angular frequency and period: "vo = xo ω (8.0) = (2.0) ω ... T = 1.57 s = 1.6 s (to 2 s.f.)"
5. Implication for Instruction
- Visual Learning: The simulation provides a visual aid for understanding abstract concepts like SHM, velocity, displacement, and the relationship between them.
- Interactive Exploration: The interactive nature of the simulation allows students to explore the concept by running simulations and perhaps modifying the values in the underlying code (though not detailed).
- Problem Solving: The source provides guided questions to encourage students to analyze the data obtained from the simulation and to calculate the period of oscillation from the values of velocity and displacement.
- Accessibility: Its platform compatibility allows for use in varied learning environments.
6. Links and Credits
- Embed Code: The source provides embed code for incorporating the simulation directly into web pages.
- Model Link: A direct link to the simulation is provided: http://iwant2study.org/ospsg/index.php/79
- Credits: The resource is credited to an author, and contact information is provided, for users who need to contact about the tool. There's a note that JavaScript must be enabled to view the email address, which suggests that there are other contact options beyond this.
- Licensing: The resources are licensed under Creative Commons Attribution-Share Alike 4.0, which allows for sharing and adapting under certain conditions.
7. Related Resources: The page is a part of a larger network of simulations, including those that deal with other aspects of SHM and also other areas of physics.
8. Conclusion This resource provides an interactive way for learners to understand the relationship between velocity and displacement in a simple harmonic motion. The example provides a way for students to work out the period of the oscillation, building on the data displayed by the simulation. The simulation is part of a large collection of learning resources on the Open Educational Resources / Open Source Physics @ Singapore platform. The source is well documented with instructions and explanations of the underlying physics.
Simple Harmonic Motion Study Guide
Quiz
- Why does the velocity vs. displacement graph for this model show two velocity values at zero displacement?
- In the context of this model, what causes there to be two displacement values at zero velocity?
- How is the angular frequency (ω) calculated in the provided solution?
- What physical quantity is represented by the variable 'xo' in the equation vo = xo ω ?
- What is the relationship between angular frequency (ω) and the period of oscillation (T)?
- Describe the motion of the body when it has a displacement of zero.
- Describe the motion of the body at the positions where displacement is at its maximum.
- In this specific model, what is the value of the maximum velocity (vo) ?
- What is the calculated period (T) of the oscillation in the simulation?
- What is the significance of the interactive simulation for understanding simple harmonic motion?
Quiz Answer Key
- The oscillating body passes through the equilibrium position (zero displacement) while moving in opposite directions. Thus, there is one positive velocity when moving right, and one negative when moving left.
- An oscillating body momentarily stops at its maximum displacement to change directions. This results in zero velocity at two points in the cycle: when it is at maximum amplitude to the left and right.
- The angular frequency (ω) is calculated by dividing the maximum velocity (vo) by the maximum displacement (xo), which is derived from the formula vo = xo ω.
- The variable 'xo' represents the maximum displacement or the amplitude of the oscillation.
- The period of oscillation (T) is inversely related to the angular frequency (ω) by the equation T = 2π/ω.
- When the body has a displacement of zero it is at the equilibrium position and is moving at its maximum speed, either to the right or to the left.
- At the positions of maximum displacement, the oscillating body has a velocity of zero momentarily as it changes direction.
- In this specific model, the maximum velocity (vo) is 8.0 (in units consistent with the model's parameters).
- The calculated period (T) of the oscillation is 1.6 seconds.
- The interactive simulation allows users to visualize and explore the relationship between velocity, displacement, and time, which enhances the understanding of SHM.
Essay Questions
- Discuss how the concepts of kinetic and potential energy are interchanged during the oscillation in this simple harmonic motion model.
- Explain how the velocity vs. position graph visually represents the characteristics of simple harmonic motion, focusing on the significance of the slope.
- Analyze how changing the spring constant (k) and the mass (m) would affect the period and the frequency of the oscillations, and describe the mathematical relationships.
- Compare and contrast the motion represented in this simulation to real world examples of simple harmonic motion and explain the limitations of the model.
- Evaluate the benefits of using interactive simulations, like this model, as a learning tool compared to traditional methods of teaching simple harmonic motion.
Glossary
Simple Harmonic Motion (SHM): A type of periodic motion where the restoring force is directly proportional to the displacement and acts in the opposite direction to that displacement, resulting in sinusoidal oscillation. Displacement (x): The distance of an object from its equilibrium position in a given direction. Velocity (v): The rate of change of displacement with respect to time, indicating both speed and direction. Equilibrium Position: The position where the net force acting on the oscillating body is zero and the body would remain at rest. Amplitude (xo): The maximum displacement of an oscillating body from its equilibrium position. Angular Frequency (ω): A measure of the rate of oscillation, expressed in radians per second; related to the frequency and period of motion. Period (T): The time taken for one complete cycle of oscillation, measured in seconds. Oscillation: A repetitive back-and-forth movement or vibration about a central position. Restoring Force: A force that always acts to push or pull an oscillating body back towards its equilibrium position. Kinetic Energy: The energy of motion of a body and is at a maximum when velocity is at a maximum. Potential Energy: The stored energy of an oscillating body that is at its maximum when displacement is at its maximum.
Frequently Asked Questions about Simple Harmonic Motion Simulation
- Why does the velocity vs. displacement graph in this simulation show two velocity values at zero displacement? The oscillating body, in this case, a mass on a spring, moves through its equilibrium position (zero displacement) in two opposite directions. When the mass is moving towards the right, it has a positive velocity. When the mass moves back through the equilibrium position towards the left, it has a negative velocity. Thus, at zero displacement, there are two possible velocity values, corresponding to the two directions of motion.
- Why are there two displacement values for zero velocity in the simulation? An oscillating body reaches zero velocity when it changes direction at its maximum displacement or amplitude. It momentarily stops before moving back in the other direction. This occurs at both the maximum positive displacement and the maximum negative displacement. Thus, there are two displacement values at zero velocity.
- How can the period of oscillation be determined using the maximum velocity from the simulation's graph? The period (T) can be calculated from the relationship between maximum velocity (vo), maximum displacement (xo), and angular frequency (ω) . The maximum velocity is given by the formula vo = xo * ω. In the given example, vo = 8.0 m/s and xo = 2.0 m, so ω can be calculated to be 4.0 rad/s. The period is then found using the formula T = 2π / ω, resulting in a period of approximately 1.57 seconds, or rounded to 1.6 seconds to 2 significant figures.
- What is the purpose of the JavaScript HTML5 applet simulation model described in the source? The simulation is an interactive educational tool designed to model and visualize simple harmonic motion (SHM). It allows users to observe how the velocity and position of a mass on a spring change over time. By displaying the velocity vs. displacement graph, it demonstrates key concepts of SHM, like the relationship between velocity and position and also provides a means to calculate the period of oscillation.
- What are some of the platform and accessibility features of this simulation model? The simulation model is designed to be highly accessible, running on various platforms including Android/iOS devices (such as smartphones and tablets), Windows/MacOSX/Linux computers (including laptops and desktops) and ChromeBook Laptops. It’s embedded in a webpage using an iframe, which makes it easily integrated into online educational resources.
- What is Easy JavaScript Simulation (EJS), and how is it used in this context? Easy JavaScript Simulation (EJS) is an authoring toolkit or software used for creating interactive simulations, in this case, for physics education. EJS is a resource development tool that allows for in-house creation of simulations that can be easily embedded in web pages or educational platforms. The provided links within the resource demonstrate a wide range of EJS applications across various subjects, suggesting its broad usability in the educational field.
- What other physics concepts or simulations are available from the same source? This source provides a vast library of simulations, including various models related to simple harmonic motion (different spring constants, initial conditions, etc.), pendulums, projectile motion, collisions, gravitational fields, and even more advanced topics like wave interference, relativity, and electromagnetism. It also includes simulations related to mathematics, and other fields showcasing a wide variety of educational tools available.
- What is the licensing for the materials, and how can they be used commercially? The content is licensed under the Creative Commons Attribution-Share Alike 4.0 Singapore License. This means that the materials can be shared and adapted, provided proper attribution is given and derivatives are also shared under a similar license. For commercial use of the EasyJavaScriptSimulations Library, users should refer to the provided link for the terms and contact This email address is being protected from spambots. You need JavaScript enabled to view it. directly to clarify permissions.
- Details
- Parent Category: 02 Newtonian Mechanics
- Category: 09 Oscillations
- Hits: 8414