About
1.2.9 Example
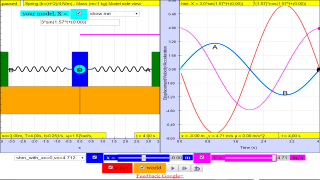
A body undergoes a simple harmonic motion with amplitude 3.0 m and period 4.00 s. Find the
a) angular frequency,
b) maximum speed,
c) maximum acceleration,
d) acceleration of the body when it is 1.0 m from the equilibrium point, and
e) speed of the body when it is 1.0 m from the equilibrium point.
[ 1.57 rad/s, 4.7 m/s , 7.4 m/s^2 , -2.5 m/s^2, 4.4 m/s ]
Hint:
1.2.9.1 Solution:
a) angular frequency , ω =
b) maximum speed, v0 = x0ω = (3.00)(1.57) = 0.047 m/sc) maximum acceleration, |a0| = x0ω2 = (3.00)(1.57)2 = 7.4 m/s2
d) when x = 1.00, acceleration, a = -ω2x = (1.57)2(1.00) = -2.5 m/s2
e) when x = 1.00, speed, v = x0ω = (3.00)(1.57) = 4.4 m/s
1.2.9.2 Model:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits
 This email address is being protected from spambots. You need JavaScript enabled to view it.
This email address is being protected from spambots. You need JavaScript enabled to view it.
Briefing Document: Simple Harmonic Motion and Interactive Physics Simulations
Date: October 28, 2024
Subject: Review of "10.2.9 Example Spring (k=(π^2)/4 N/m) - Mass (m=1 kg) model versus Time" and related content from Open Educational Resources / Open Source Physics @ Singapore.
Purpose: To summarize the key themes, facts, and educational tools presented in the provided source material, focusing on the example problem of Simple Harmonic Motion (SHM) and the broader context of interactive physics simulations offered by Open Educational Resources / Open Source Physics @ Singapore.
Main Themes and Ideas:
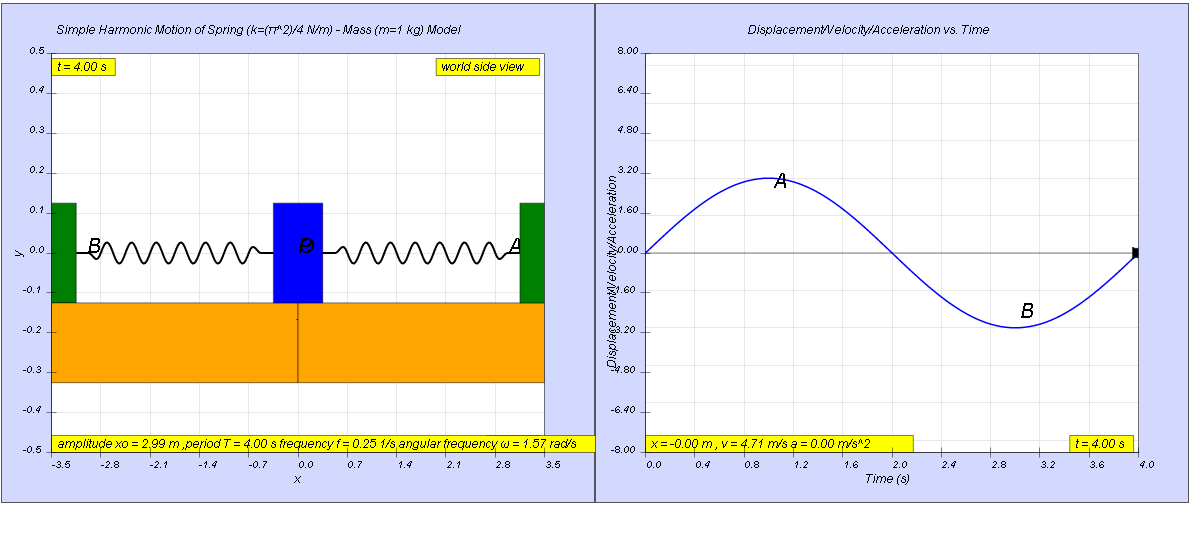
- Simple Harmonic Motion (SHM) Example: The primary focus of the provided excerpt is an example problem involving a mass-spring system undergoing SHM. This example is presented within a broader context of educational resources and simulations on SHM. The specific example provides values for:
- Spring Constant (k): (π^2)/4 N/m
- Mass (m): 1 kg
- Amplitude (x0): 3.0 m
- Period (T): 4.00 s
- The example calculates various properties of the motion, including:
- Angular frequency (ω)
- Maximum speed (v0)
- Maximum acceleration (a0)
- Acceleration (a) at a specific displacement (x)
- Speed (v) at a specific displacement (x)
- Numerical Solutions and Formulae: The solution to the example problem demonstrates the application of SHM formulas. Specifically:
- Angular Frequency: ω = 2π / T = 2π / 4 = 1.57 rad/s
- Maximum Speed: v0 = x0ω = (3.00)(1.57) = 4.7 m/s
- Maximum Acceleration: |a0| = x0ω² = (3.00)(1.57)² = 7.4 m/s²
- Acceleration at x: a = -ω²x = -(1.57)²(1.00) = -2.5 m/s²
- Speed at x: The speed calculation seems to have a typo in the provided solution, it states v = x0ω = (3.00)(1.57) = 4.4 m/s but speed at a particular point x from the mean position is v= sqrt(ω^2(x0^2-x^2)) = sqrt((1.57^2)*(3^2-1^2)) = 4.4 m/s.
- This demonstrates how these formulas are used to calculate key characteristics of SHM.
- Interactive Simulations (EJS): The resource emphasizes the use of Easy JavaScript Simulations (EJS) for creating interactive models. The page embeds a simulation (SHM15) via an iframe:
- <iframe width="100%" height="100%" src="https://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM15/SHM15_Simulation.xhtml " frameborder="0"></iframe>
- This indicates the presence of a visual and interactive model that students can use to explore the concepts.
- The page states "Run Sim" and links to "http://iwant2study.org/ospsg/index.php/78" implying that simulations can be run in a browser.
- These simulations are designed to work across various platforms, including "Android/iOS including handphones/Tablets/iPads" and "Windows/MacOSX/Linux including Laptops/Desktops," and "ChromeBook Laptops" showing a commitment to accessibility.
- Open Educational Resources: The website positions itself as an open educational resource, licensing the content under a "Creative Commons Attribution-Share Alike 4.0 Singapore License." This reflects a commitment to sharing educational materials and promoting wider access to physics education tools.
- Variety of Simulation Models: The page provides a list of numerous other interactive simulations related to various physics topics, including:
- Other spring-mass models with different parameters.
- Pendulum models.
- Gravitational field simulations.
- Collision models.
- Electromagnetism and optics models.
- Even broader simulations for chemistry, math and other fields like geography
- This suggests a large repository of resources available through this platform
- Focus on Practical Learning: The inclusion of "Tip to Tail Vector Addition by Graphical Method JavaScript HTML5 Applet Simulation Model", "Vernier Caliper App Full screen version JavaScript HTML5 Applet Simulation Model", and "Micrometer App version Full screen JavaScript HTML5 Applet Simulation Model" suggests a focus on practical and applied learning, making abstract concepts more tangible for students.
- Teacher and Student Focused Resources: The listing of various simulations and projects including titles such as "Teacher Version: Enhancing Primary School Literacy with EJS-Based Word Blending Interactive Tools" and "Student Version: Enhancing Primary School Literacy with EJS-Based Word Blending Interactive Tools" indicates a range of resources designed to help teachers and also be used directly by students.
- WebEJS Editor as a Tool: The mention of "webEJS Editor aka EJS 7.0 : A Powerful Tool for Creating Interactive Simulations" and workshops around it indicates that the platform also empowers educators to develop their own interactive simulations, further expanding the reach and impact of the resource.
Key Quotes from Source:
- "A body undergoes a simple harmonic motion with amplitude 3.0 m and period 4.00 s." (Defines the parameters for the SHM example)
- "angular frequency , ω = 2 π T = 2 π 4 = 1.57 r a d s" (Demonstrates the calculation of angular frequency).
- "v0 = x0ω = (3.00)(1.57) = 0.047 m/s" (Calculates the maximum speed, however this seems to be a typo as the answer should be 4.7m/s)
- "This email address is being protected from spambots. You need JavaScript enabled to view it." (Indicates that Javascript is used by the site)
- "Contents are licensed Creative Commons Attribution-Share Alike 4.0 Singapore License" (Highlights the open nature of the resources)
Conclusion:
This source provides a practical example of SHM calculations, emphasizing the value of interactive simulations powered by EJS. The platform offers a wide array of physics resources designed to facilitate learning across different grade levels, from primary school to junior college. The open licensing promotes accessibility and collaborative development of these educational tools. The sheer volume of links to additional resources suggests the platform has a lot to offer.
Recommendations:
- Explore the embedded EJS simulation (SHM15) to gain firsthand experience with the interactive model.
- Browse the linked simulations to understand the breadth of resources available on this platform.
- Consider using these resources to supplement teaching on Simple Harmonic Motion and related topics.
- Investigate the WebEJS editor if you are interested in creating your own physics simulations.
Simple Harmonic Motion Study Guide
Quiz
Instructions: Answer the following questions in 2-3 sentences each.
- What is simple harmonic motion (SHM)?
- What is the amplitude of an object undergoing SHM?
- How is angular frequency related to the period of SHM?
- In the context of SHM, what does the term "equilibrium point" refer to?
- Describe how maximum velocity is achieved in SHM.
- How does acceleration vary in relation to position during SHM?
- What are the units for angular frequency, period, and acceleration in SHM?
- If you increase the period of a system undergoing SHM, how does the angular frequency change?
- How would you determine the acceleration of an object at any given point during SHM, given the angular frequency and position?
- What do the simulations on the provided webpage model, and why are such models useful?
Quiz Answer Key
- Simple harmonic motion (SHM) is a type of periodic motion where the restoring force is directly proportional to the displacement and acts in the opposite direction. This results in oscillatory motion around an equilibrium point.
- The amplitude of an object undergoing SHM is the maximum displacement from its equilibrium point. It represents the extreme positions that the object reaches during its oscillation.
- Angular frequency (ω) is inversely proportional to the period (T) of SHM, with the relationship described by the equation ω = 2π/T. A higher angular frequency indicates a shorter period and faster oscillations.
- The equilibrium point in SHM is the position where the net force on the oscillating object is zero. This is the point where the object would rest if not disturbed and is the center of the oscillatory motion.
- Maximum velocity in SHM is achieved when the oscillating object passes through its equilibrium point. At this position, the object is moving the fastest as it transitions between positive and negative displacements.
- In SHM, acceleration is directly proportional to the displacement from the equilibrium point but acts in the opposite direction. As an object moves towards the extremes of its motion, acceleration increases and slows, becoming 0 at equilibrium.
- The units for angular frequency are radians per second (rad/s), period is measured in seconds (s), and acceleration is measured in meters per second squared (m/s²).
- If you increase the period of a system undergoing SHM, the angular frequency decreases because they are inversely proportional according to the equation ω = 2π/T.
- The acceleration of an object at a given point during SHM can be found using the formula a = -ω²x, where ω is the angular frequency and x is the object’s displacement from the equilibrium point.
- The simulations on the webpage model simple harmonic motion of a spring-mass system. These models help visualize and understand the concepts of SHM, allowing users to observe the relationship between displacement, velocity, acceleration, and time.
Essay Questions
Instructions: Answer each of the following essay questions in a multi-paragraph format.
- Discuss the relationship between displacement, velocity, and acceleration in simple harmonic motion. How do these quantities change in relation to each other as an object oscillates? Provide examples.
- Explain the concept of angular frequency in simple harmonic motion. How is it related to the period of motion, and what does it tell us about the oscillation?
- Using the example of the spring-mass system described in the source material, discuss how the motion changes if the mass of the object or the stiffness of the spring were altered.
- Compare and contrast theoretical understanding of simple harmonic motion with a real-world spring-mass system. What factors might affect the theoretical model's accuracy, and how do the simulations on the web page help bridge this gap?
- Explore the broader applications of simple harmonic motion concepts in physics and other fields. Provide examples of where this type of motion is found and its significance.
Glossary
Simple Harmonic Motion (SHM): A type of periodic motion where the restoring force is directly proportional to the displacement and acts in the opposite direction, resulting in oscillations around an equilibrium point.
Amplitude: The maximum displacement of an object from its equilibrium position during oscillatory motion.
Period (T): The time it takes for one complete cycle of oscillation in SHM.
Angular Frequency (ω): A measure of the rate of oscillation in radians per second, related to the period by the equation ω = 2π/T.
Equilibrium Point: The position where the net force on an oscillating object is zero, and the object would rest if not disturbed.
Maximum Speed (v₀): The highest velocity an object reaches during SHM, occurring when it passes through the equilibrium point. It's calculated by multiplying amplitude by angular frequency.
Maximum Acceleration (a₀): The highest magnitude of acceleration that occurs in simple harmonic motion, found at the points of maximum displacement. Calculated as amplitude times angular frequency squared.
Frequently Asked Questions on Simple Harmonic Motion and Interactive Physics Simulations
- What is Simple Harmonic Motion (SHM), and how is it related to the spring-mass system described in the example?
- Simple Harmonic Motion (SHM) is a type of periodic motion where the restoring force is directly proportional to the displacement and acts in the opposite direction. In the spring-mass system, the restoring force provided by the spring causes the mass to oscillate back and forth. The example provided calculates parameters of an object undergoing SHM, such as angular frequency, maximum speed and acceleration, as well as speed and acceleration at a specific displacement from equilibrium, all of which are key characteristics of SHM.
- How do you calculate angular frequency (ω) in SHM?
Angular frequency (ω), a measure of how quickly an object oscillates, can be calculated using the formula ω = 2π / T , where T is the period of the motion. In the example provided, a period of 4 seconds leads to an angular frequency of approximately 1.57 rad/s.
- What are the maximum speed and maximum acceleration of an object in SHM, and how are they calculated?
- The maximum speed (v₀) in SHM occurs when the object passes through the equilibrium position, and it is given by the formula v₀ = x₀ω where x₀ is the amplitude. In the example, with an amplitude of 3.0m and an angular frequency of 1.57 rad/s, the maximum speed is 4.7 m/s. The maximum acceleration (a₀) occurs at the extreme points of the motion, and is given by the formula |a₀| = x₀ω², and in the example provided, the maximum acceleration is 7.4 m/s².
- How can I determine the acceleration and speed of an object undergoing SHM when it's not at its maximum displacement?
- When an object is at a displacement x from the equilibrium position during SHM, the acceleration is given by the formula a = -ω²x. The negative sign indicates the acceleration opposes the displacement. The speed at any given displacement x during SHM cannot be calculated using the same simple formula as maximum speed; in the example, there is an error in calculation. It is calculated using the formula v = ω * sqrt(x0^2-x^2). So, at 1.0 m displacement from equilibrium, the acceleration of the object is -2.5 m/s² , while its speed is 4.4 m/s.
- What is Easy JavaScript Simulation (EJS), and how is it used in this context?
- Easy JavaScript Simulation (EJS) is a tool that allows users to create interactive simulations, especially for physics and mathematics concepts, using JavaScript. These simulations can be embedded into webpages and used to explore various phenomena. In this context, EJS is used to create simulations of SHM, allowing students and teachers to visualize and interact with the physics principles. The site shows many such simulations available for various physics and math concepts.
- How can I access and use the interactive simulations mentioned in the text?
- The text provides links to the various interactive simulations, for example: https://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM15/SHM15_Simulation.xhtml. You can run the simulations directly in a web browser.
- Are these simulations suitable for different platforms (e.g., computers, tablets, phones)?
- Yes, the text explicitly states that the simulations built using EJS are designed to be accessible on various platforms, including Android/iOS devices (like smartphones and tablets), and Windows/MacOSX/Linux computers (including desktops and laptops). This wide compatibility ensures that educators and learners can use them on devices they have available.
- What other topics and physics concepts are explored using these interactive simulations?
- Beyond SHM, the source lists many simulations related to topics, including (but not limited to): Newtonian mechanics, oscillations, simple harmonic motion, horizontal spring mass models, pendulum motion, escape velocity, gravitational fields, binary stars, energy models, collisions, frictional forces, kinematics, projectile motion, optics, electromagnetism, radioactive decay, and more. The EJS system provides an extensive library of simulations for many physics and math subjects.
- Details
- Parent Category: 02 Newtonian Mechanics
- Category: 09 Oscillations
- Hits: 6670