
About
Tracker Modeling in Spring Mass System
For Teachers
Credits
Author: lookang model, jitning video
Contact: This email address is being protected from spambots. You need JavaScript enabled to view it.
Document Brief: Modeling a Spring-Mass System Using Tracker
This document analyzes the oscillatory motion of a spring-mass system using Tracker software. The study focuses on simple harmonic motion (SHM), with the spring force modeled as proportional to displacement from equilibrium (F=−k⋅x) and damping effects observed through velocity (v) decay.
Purpose:
To study the periodic motion of a spring-mass system, validate Hooke’s law, and analyze damping effects through experimental data and theoretical modeling.
Key Features:
- Analysis of displacement (y), velocity (vy), and time (t).
- Application of force functions:
- Restoring force: Fy=−k⋅y,
- Damping force: Fd=−w⋅vy.
- Validation of simple harmonic motion parameters.
Study Guide: Modeling Spring-Mass Oscillations
Learning Objectives:
- Understand the relationship between spring force, displacement, and damping in SHM.
- Analyze displacement and velocity graphs to identify key SHM characteristics.
- Validate Hooke’s law using experimental data and theoretical predictions.
Step-by-Step Guide:
-
Setup and Calibration:
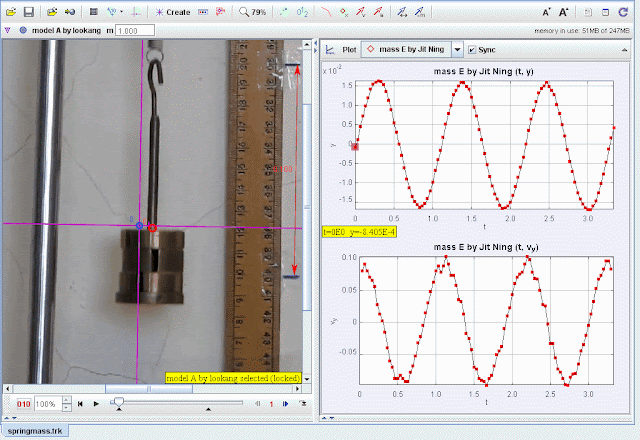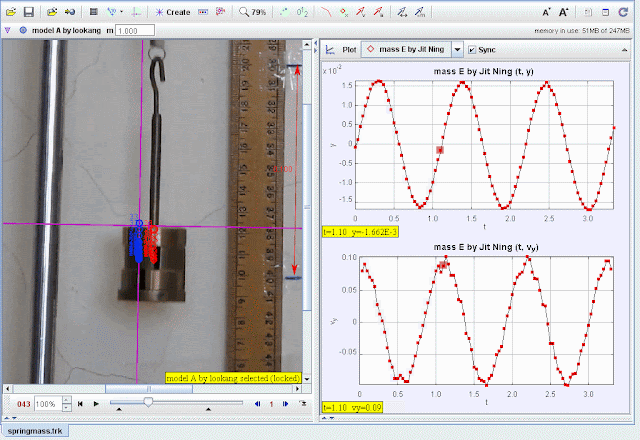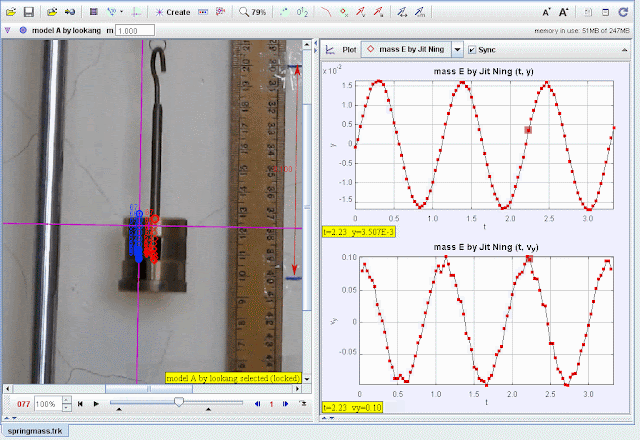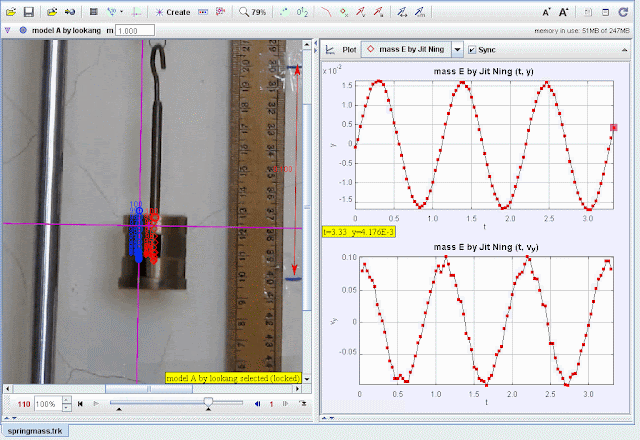
- Import the video of the spring-mass system into Tracker.
- Calibrate the scale using the ruler visible in the video for accurate measurements.
-
Tracking Motion:
- Track the vertical position (y) of the mass frame by frame.
- Record displacement and velocity data for a full oscillatory cycle.
-
Define Force Functions:
- Open Tracker’s Model Builder and set the following:
- Parameters:
- w=5.795 rad/s (angular frequency),
- m=1.0 kg (mass).
- Force functions:
- Fy=−w^2⋅y−w⋅vy (restoring and damping force).
- Parameters:
- Open Tracker’s Model Builder and set the following:
-
Graphical Analysis:
- Plot y-displacement vs. t:
- Verify sinusoidal motion characteristic of SHM.
- Plot vy- velocity vs. t:
- Observe the velocity oscillations and damping effects.
- Compare experimental data (red points) with the theoretical model (blue curve).
- Plot y-displacement vs. t:
-
Applications:
- Study SHM in mechanical and physical systems.
- Explore the effect of damping on oscillatory motion.
Tips for Success:
- Ensure accurate tracking of the mass’s vertical position.
- Validate theoretical parameters by comparing experimental data to modeled motion.
FAQ: Spring-Mass System Modeling
1. What forces act on the spring-mass system?
- Restoring force Fy=−k⋅y pulls the mass back to equilibrium.
- Damping force Fd=−w⋅vy resists motion, reducing amplitude over time.
2. How is SHM modeled?
SHM is modeled using:
Fy=−k⋅y
where k=w2⋅m is the spring constant. The position function is:
y(t)=A⋅cos(wt+ϕ)
3. What does the displacement graph show?
The displacement graph shows sinusoidal motion, indicating periodic oscillations with gradually decreasing amplitude due to damping.
4. How is damping incorporated?
Damping is added to the force equation as:
Fd=−w⋅vy
which reduces the system’s energy, causing the amplitude to decay exponentially.
5. What is the role of angular frequency (w)?
Angular frequency determines the oscillation speed and is related to the spring constant and mass by:
w=km
6. Can energy conservation be applied?
Energy in SHM alternates between kinetic and potential forms. Damping results in energy loss, which can be calculated as the difference between initial and final mechanical energy.
7. What are practical applications of spring-mass systems?
- Designing mechanical oscillators like shock absorbers.
- Studying vibrations in structures and materials.
- Analyzing biological systems like muscle elasticity.
- Details
- Parent Category: 02 Newtonian Mechanics
- Category: 09 Oscillations
- Hits: 7520
