About
Topics
KinematicsSpeed, velocity and acceleration
Graphical analysis of motion
Free-fall
Effect of air resistance
Description
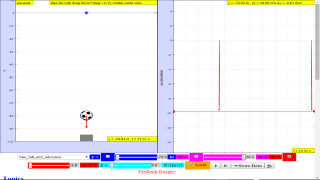
This simulation has a drop-down menu for exploration of(ii) moving with uniform velocity, use of progressive mathematical model is encouraged
(iii) moving with non-uniform velocity (eg, constant acceleration) use of progressive mathematical model is encouraged
When only the velocity-time graph check-box is selected, it can be explored for the following cases too.
(ii) moving with uniform velocity (eg, no acceleration) model of the form Y = Y0+u*t
(iii) moving with uniform acceleration (eg, constant acceleration = 9.81 m/s^2) model of the form Y = Y0+u*t+0.5*g*t
(iv) moving with non-uniform acceleration (eg, with small ot large drag force acting thus acceleration changes).
The default acceleration is set at-9.81 m/s^2 which is near to the Earth is constant and is approximately 10 m/s 2.
Lastly, by selecting the 3 options of
"free fall"
"free_fall_with_small_air_resistance"
"free_fall_with_large_air_resistance"
It can provide the experience and evidences for describing the motion of bodies with constant weight falling with (large and small) or without air resistance, including reference to terminal velocity, a constant velocity as a result of balanced forces of weight of mass and the drag force giving rise to zero acceleration.
Sample Learning Goals
(f) deduce from the shape of a displacement-time graph when a body is:
(ii) moving with uniform velocity
(iii) moving with non-uniform velocity
(g) deduce from the shape of a velocity-time graph when a body is:
(ii) moving with uniform velocity
(iii) moving with uniform acceleration
(iv) moving with non-uniform acceleration
(i) state that the acceleration of free fall for a body near to the Earth is constant and is approximately 10 m/s 2
(j) describe the motion of bodies with constant weight falling with or without air resistance, including reference to terminal velocity
Version:
ball taken from: http://psychology.wikia.com/wiki/File:Soccer_ball.svg
http://weelookang.blogspot.sg/2013/12/ejss-free-fall-model.htmlFor Teachers
Teacher-Submitted Activities
|
Title |
Authors |
Level |
Type |
Updated |
Share an activity! email
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits
 This email address is being protected from spambots. You need JavaScript enabled to view it.
This email address is being protected from spambots. You need JavaScript enabled to view it.
Briefing Document: Free Fall Simulation Model
1. Overview
This document reviews a JavaScript HTML5 applet simulation model designed to teach secondary-level kinematics, focusing specifically on motion in the vertical (Y) direction, commonly known as free fall. The simulation allows users to explore various scenarios of motion, with and without air resistance, using interactive graphs and visual representations. The resources includes teacher guides, worksheets, examples, and multiple versions of the model. This interactive tool aims to enhance understanding of concepts related to displacement, velocity, acceleration, and terminal velocity.
2. Key Themes & Concepts
- Kinematics in One Dimension: The simulation primarily focuses on motion in a single (vertical) dimension, allowing students to understand the relationships between position, velocity, and acceleration in a simplified context.
- Free Fall: A core concept addressed is free fall, which is defined as the motion of an object under the influence of gravity alone (ignoring air resistance). This is shown with the option for "free fall".
- Influence of Air Resistance: The simulation also includes scenarios with small and large air resistance. This allows users to see how these forces affect motion and leads to the understanding of terminal velocity.
- Graphical Analysis of Motion: A major emphasis is placed on the use of displacement-time and velocity-time graphs. Students are guided to interpret these graphs and extract information about the motion of the simulated object.
- Mathematical Modeling: The simulation uses and encourages the use of mathematical models to represent the different motion scenarios. The mathematical form of these models include:
- Y = 0 (object at rest)
- Y = Y0 + u*t (uniform velocity)
- Y = Y0 + ut + 0.5g*t^2 (uniform acceleration)
- And more complex models when air resistance is taken into account.
- Terminal Velocity: The simulation allows users to see how air resistance affects a falling object and the resulting terminal velocity - where the forces of weight and drag are balanced and acceleration becomes zero.
3. Simulation Features and Functionality
- Drop-Down Menu: The simulation utilizes a drop-down menu to allow users to choose from various initial conditions:
- Object at rest.
- Object moving with uniform velocity.
- Object moving with non-uniform velocity (constant acceleration).
- Graphing Options: The simulation allows the user to view either only velocity-time graph or a combination of velocity-time and displacement-time graphs, allowing focus on specific learning outcomes.
- Air Resistance Options: The simulation has options to include or exclude air resistance and to choose between small or large air resistance.
- Default Acceleration: The default value for the acceleration due to gravity is set at approximately -9.81 m/s², which can be rounded to -10 m/s², which is suitable for earth based experiments.
- Embeddable: The simulation can be embedded into a web page using an iframe, making it easy to integrate into online learning environments.
4. Learning Goals
The simulation's primary learning goals include enabling students to:
- "(e) plot and interpret a displacement-time graph and a velocity-time graph"
- "(f) deduce from the shape of a displacement-time graph when a body is: (i) at rest (ii) moving with uniform velocity (iii) moving with non-uniform velocity"
- "(g) deduce from the shape of a velocity-time graph when a body is: (i) at rest (ii) moving with uniform velocity (iii) moving with uniform acceleration (iv) moving with non-uniform acceleration"
- "(i) state that the acceleration of free fall for a body near to the Earth is constant and is approximately 10 m/s 2"
- "(j) describe the motion of bodies with constant weight falling with or without air resistance, including reference to terminal velocity"
These goals focus on enhancing graph interpretation skills as well as understanding free-fall concepts with an awareness of the effects of air resistance.
5. Examples and Activities
- Skydiver Example: The provided example involves two skydivers jumping at different times. This helps illustrate that the difference in velocity between two objects experiencing the same acceleration is constant, while the distance between the two skydivers increases over time.
- "Does the difference in their speeds stay the same throughout the fall?" suggested answer: after t =2 s, the difference is always the same difference as shown by the constant difference.
- "Does the vertical distance between them stay the same throughout the fall?" suggested answer: after t =2 s, the difference in position increases as shown by the increasing difference of YELLOW minus BLUE line.
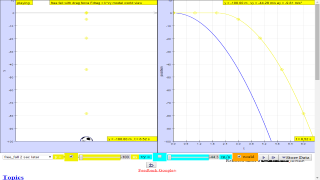
- Tennis Ball Example: This more complex example involves a tennis ball thrown upwards from the top of a building and asks questions about the time to maximum height, max height, the time to return to start height, the velocity at return, and position and velocity at a specific time.
- a.the time at which the ball reaches its maximum height suggested answer: t = 2.0 s
- b.the maximum height suggested answer: H maximum = 70.4 m
- c.the time at which the ball returns to the height from which it was thrown suggested answer: t = 4.0 or 4.1 s
- d.the velocity of the ball at this instant suggested answer: v = -20.2 m/s
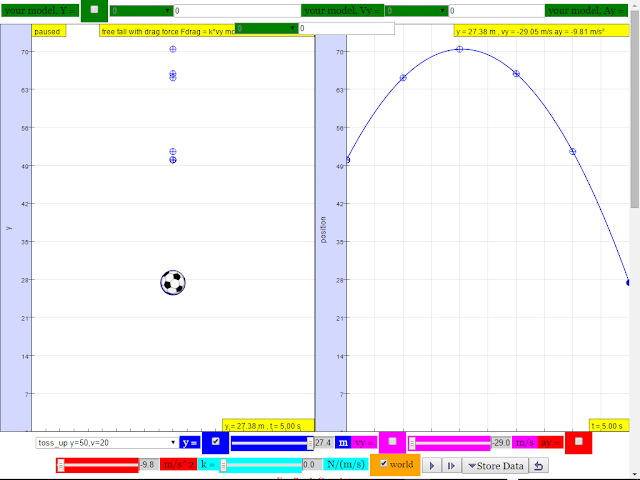
- e.the velocity and position of the ball at t = 5 s suggested answer: y = 27.4 m and v = -29.1 m/s
6. Supplementary Resources
The document provides links to many supplementary materials and related work including:
- Worksheets: A motion in one dimension student worksheet is available.
- Blog Posts: Numerous blog posts by "weelookang" detailing development, versions, and applications of the simulation.
- Other Simulations: Links to other simulations related to kinematics and physics concepts, including projectile motion, energy models, and gravity, are also provided.
- Teacher Resources: A section dedicated to teachers, including information on how to share activities and resources.
- Project Information: Details on a project, "Understanding Teacher Learning Community as Support for Implementation of Open Source Physics for Conceptual Instruction", that uses the simulation.
7. Versions
The simulation has had numerous iterations, this is documented with the various blog posts by "weelookang".
8. Conclusion
The "Secondary Kinematics in Y direction or Free Fall JavaScript HTML5 Applet Simulation Model" is a comprehensive educational tool. Its interactive nature, combined with focused learning goals, supplementary resources, and detailed examples, makes it a strong resource for teaching and learning kinematics, free fall, and the effects of air resistance. The multiple versions of the simulation and related resources demonstrate ongoing development and refinement of the tool. The use of EasyJavaScriptSimulations library under a Creative Commons License allows for the simulation to be freely used. The detailed documentation and related resources make it easy to use by educators.
Free Fall and Kinematics Study Guide
Quiz
- What does the simulation allow you to explore regarding motion?
- The simulation allows exploration of motion at rest, with uniform velocity, with non-uniform velocity including constant acceleration, and with varied air resistance, each case through graphical analysis.
- What are the three specific free-fall scenarios available in the simulation, and what does each show?
- The three free-fall options are "free fall," "free fall with small air resistance," and "free fall with large air resistance," which help illustrate the effects of air resistance on a falling body, including reaching terminal velocity.
- What is the default acceleration in the simulation, and what does it represent?
- The default acceleration in the simulation is -9.81 m/s², representing the approximate acceleration due to gravity near the Earth's surface. This is the constant rate at which objects accelerate downward in free fall.
- What is terminal velocity?
- Terminal velocity is the constant speed that a freely falling object eventually reaches when the force of air resistance equals the force of gravity, resulting in zero acceleration.
- How can the displacement-time graph help in understanding motion?
- The shape of a displacement-time graph can help determine if a body is at rest (horizontal line), moving with uniform velocity (straight, diagonal line), or moving with non-uniform velocity (curved line).
- How can the velocity-time graph help in understanding motion?
- The shape of a velocity-time graph can help determine if a body is at rest (horizontal line at zero velocity), moving with uniform velocity (horizontal line above zero), moving with uniform acceleration (straight, diagonal line), or moving with non-uniform acceleration (curved line).
- What does the simulation show about the acceleration of free fall near the Earth?
- The simulation confirms that the acceleration of free fall for a body near the Earth is constant, approximately 10 m/s², which is the effect of gravity on a falling object.
- According to the example problem with two skydivers, what happens to the difference in their speeds?
- In the absence of air resistance, the difference in speeds between two skydivers remains the same throughout the fall due to the constant acceleration of gravity.
- According to the example problem with two skydivers, what happens to the vertical distance between the skydivers?
- The vertical distance between the two skydivers increases as time progresses because the leading skydiver has a greater speed at any given moment and travels a greater distance in the same amount of time.
- In the tennis ball example, what is the velocity of the ball when it returns to the thrower’s hand?
- When a tennis ball returns to the height from which it was thrown, its velocity will be equal in magnitude, but opposite in direction, to its initial velocity, if air resistance is negligible.
Answer Key
- The simulation allows exploration of motion at rest, with uniform velocity, with non-uniform velocity including constant acceleration, and with varied air resistance, each case through graphical analysis.
- The three free-fall options are "free fall," "free fall with small air resistance," and "free fall with large air resistance," which help illustrate the effects of air resistance on a falling body, including reaching terminal velocity.
- The default acceleration in the simulation is -9.81 m/s², representing the approximate acceleration due to gravity near the Earth's surface. This is the constant rate at which objects accelerate downward in free fall.
- Terminal velocity is the constant speed that a freely falling object eventually reaches when the force of air resistance equals the force of gravity, resulting in zero acceleration.
- The shape of a displacement-time graph can help determine if a body is at rest (horizontal line), moving with uniform velocity (straight, diagonal line), or moving with non-uniform velocity (curved line).
- The shape of a velocity-time graph can help determine if a body is at rest (horizontal line at zero velocity), moving with uniform velocity (horizontal line above zero), moving with uniform acceleration (straight, diagonal line), or moving with non-uniform acceleration (curved line).
- The simulation confirms that the acceleration of free fall for a body near the Earth is constant, approximately 10 m/s², which is the effect of gravity on a falling object.
- In the absence of air resistance, the difference in speeds between two skydivers remains the same throughout the fall due to the constant acceleration of gravity.
- The vertical distance between the two skydivers increases as time progresses because the leading skydiver has a greater speed at any given moment and travels a greater distance in the same amount of time.
- When a tennis ball returns to the height from which it was thrown, its velocity will be equal in magnitude, but opposite in direction, to its initial velocity, if air resistance is negligible.
Essay Questions
- Discuss how the free-fall simulation can be used to demonstrate the difference between uniform and non-uniform velocity. Use examples from the simulation's different modes and graph options to support your points.
- Analyze the concept of terminal velocity using the simulation. How does the simulation model air resistance and its effects on a falling object's velocity? How do the different free-fall scenarios (no air resistance, small, and large air resistance) contribute to understanding this concept?
- Explain the relationships between displacement, velocity, and acceleration as represented in the simulation’s graphs. How do these relationships change under conditions of rest, uniform velocity, uniform acceleration, and non-uniform acceleration?
- Using examples from the provided text, discuss how the simulation enhances the learning of kinematics concepts for students, with specific reference to the sample learning goals.
- How does the simulation provide evidence for the learning of these concepts: (i) the acceleration of free fall near Earth is constant at approximately 10 m/s²; and (ii) the description of the motion of bodies with constant weight falling with or without air resistance including reference to terminal velocity.
Glossary of Key Terms
- Kinematics: The study of motion, focusing on displacement, velocity, and acceleration, without considering the forces that cause the motion.
- Uniform Velocity: Motion at a constant speed in a straight line, with no change in direction or rate of movement.
- Non-uniform Velocity: Motion where the speed or direction of the moving object changes over time.
- Acceleration: The rate of change of velocity over time, which can involve changes in speed, direction, or both.
- Free Fall: The motion of an object under the influence of gravity alone, with no other forces acting upon it, such as air resistance.
- Terminal Velocity: The constant speed that a freely falling object eventually reaches when the force of air resistance equals the force of gravity, resulting in zero acceleration.
- Displacement-Time Graph: A graph that shows the position of an object over time, with the slope of the graph representing the object's velocity.
- Velocity-Time Graph: A graph that shows the velocity of an object over time, with the slope of the graph representing the object's acceleration and the area under the graph representing the object's displacement.
- Air Resistance: The force that opposes the motion of an object through the air, which is dependent on the object's speed, shape, and the air density.
- Constant Acceleration: A type of motion in which the velocity of an object changes at a steady rate.
Worksheet
Examples
From Dave and Gavin,
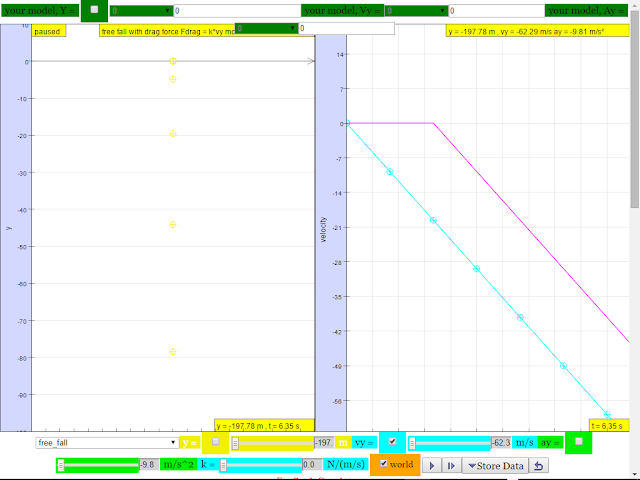
1.A sky diver jumps out of a hovering helicopter. A 2 seconds afterwards another sky diver jumps out and they both fall along the same vertical line. Ignore air resistance so that both sky divers fall with the same acceleration.
a.Does the difference in their speeds stay the same throughout the fall?
 |
| https://sg.iwant2study.org/ospsg/index.php/interactive-resources/physics/02-newtonian-mechanics/01-kinematics/37-kinematics-in-y-direction |
suggested answer: after t =2 s, the difference is always the same difference as shown by the constant difference.
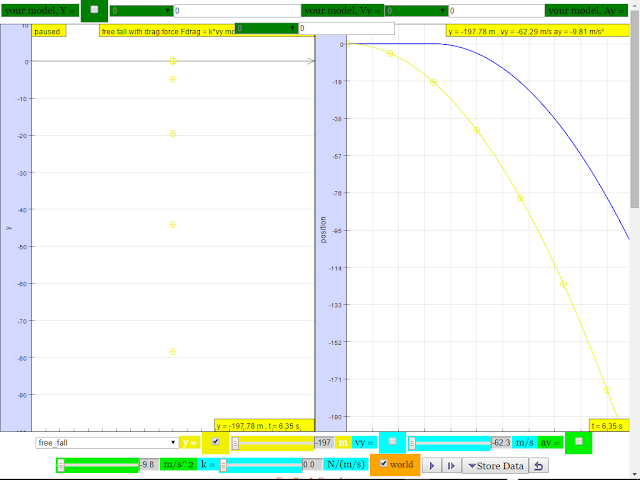
b.Does the vertical distance between them stay the same throughout the fall?
 |
| https://sg.iwant2study.org/ospsg/index.php/interactive-resources/physics/02-newtonian-mechanics/01-kinematics/37-kinematics-in-y-direction |
suggested answer: after t =2 s, the difference in position increases as shown by the increasing difference of YELLOW minus BLUE line.
Question 2
2.A tennis ball thrown from the top of a building is given an initial velocity of 20 m/s straight upward. The building is 50 m high, and the ball just misses the edge of the roof on its way down. Using t = 0 as the time the ball leaves the thrower’s hand, determine
a.the time at which the ball reaches its maximum height
 |
| https://sg.iwant2study.org/ospsg/index.php/interactive-resources/physics/02-newtonian-mechanics/01-kinematics/37-kinematics-in-y-direction |
suggested answer: t = 2.0 s
b.the maximum height
suggested answer: H maximum = 70.4 m
c.the time at which the ball returns to the height from which it was thrown
 |
| https://sg.iwant2study.org/ospsg/index.php/interactive-resources/physics/02-newtonian-mechanics/01-kinematics/37-kinematics-in-y-direction |
suggested answer: t = 4.0 or 4.1 s
d.the velocity of the ball at this instant
suggested answer: v = -20.2 m/s
e.the velocity and position of the ball at t = 5 s
 |
| https://sg.iwant2study.org/ospsg/index.php/interactive-resources/physics/02-newtonian-mechanics/01-kinematics/37-kinematics-in-y-direction |
Versions
- http://weelookang.blogspot.sg/2016/01/ejss-free-fall-simulation-added-more.html Blogpost on more cases added
- http://weelookang.blogspot.sg/2014/03/ejss-kinematics-in-y-model.html Blogpost on JavaScript version by Loo Kang Wee
- http://weelookang.blogspot.sg/2013/12/ejss-free-fall-model.html Blogpost on JavaScript version by Loo Kang Wee
- http://weelookang.blogspot.sg/2013/12/ejss-kinematics-model.html template objects from lookang
- http://weelookang.blogspot.sg/2010/09/ejs-open-source-bouncing-ball-with-drag.html Blogpost on Java vesion by Loo Kang Wee and Fu-Kwun Hwang
- http://weelookang.blogspot.sg/2010/06/ejs-open-source-kinematics-java-applet.html
- http://www.compadre.org/osp/items/detail.cfm?ID=13050 Physlet One-Dimensional Kinematics Illustrations Package by Andreu Glasmann, Wolfgang Christian, and Mario Belloni
Other Resources
- http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=421.0 Elastic bouncing ball Java Version by Fu-Kwun Hwang
- http://butikov.faculty.ifmo.ru/Projects/Falling_bodies.html#_applet Falling Object Java 3D version by Eugene Butikov
- http://www.opensourcephysics.org/items/detail.cfm?ID=10001 Free Fall Model by Andrew Duffy
Other Hands-on kit
- https://sites.google.com/site/iprofmeca/session-1-free-fall by This email address is being protected from spambots. You need JavaScript enabled to view it.
Project related:
Understanding Teacher Learning Community as Support for Implementation of Open Source Physics for Conceptual Instruction
Project Number: OER 10/15 GWF
Project Duration: 01 July 2015 - 30 April 2017
http://weelookang.blogspot.sg/2015/07/understanding-teacher-learning.html
Family of Resources
| Primary | Junior College | ||||||||||||||||||||||||||||||||||||||||
About
TopicsKinematicsSpeed, velocity and acceleration Graphical analysis of motion Free-fall Effect of air resistance DescriptionThis simulation has a drop-down menu for exploration of(ii) moving with uniform velocity, use of progressive mathematical model is encouraged (iii) moving with non-uniform velocity (eg, constant acceleration) use of progressive mathematical model is encouraged When only the velocity-time graph check-box is selected, it can be explored for the following cases too. (ii) moving with uniform velocity (eg, no acceleration) model of the form Y = Y0+u*t (iii) moving with uniform acceleration (eg, constant acceleration = 9.81 m/s^2) model of the form Y = Y0+u*t+0.5*g*t (iv) moving with non-uniform acceleration (eg, with small ot large drag force acting thus acceleration changes). The default acceleration is set at-9.81 m/s^2 which is near to the Earth is constant and is approximately 10 m/s 2. Lastly, by selecting the 3 options of "free fall" "free_fall_with_small_air_resistance" "free_fall_with_large_air_resistance" It can provide the experience and evidences for describing the motion of bodies with constant weight falling with (large and small) or without air resistance, including reference to terminal velocity, a constant velocity as a result of balanced forces of weight of mass and the drag force giving rise to zero acceleration. Sample Learning Goals
(e) plot and interpret a displacement-time graph and a velocity-time
graph
(f) deduce from the shape of a displacement-time graph when a body is: (ii) moving with uniform velocity (iii) moving with non-uniform velocity (g) deduce from the shape of a velocity-time graph when a body is: (ii) moving with uniform velocity (iii) moving with uniform acceleration (iv) moving with non-uniform acceleration (i) state that the acceleration of free fall for a body near to the Earth is constant and is approximately 10 m/s 2 (j) describe the motion of bodies with constant weight falling with or without air resistance, including reference to terminal velocity Version:ball taken from: http://psychology.wikia.com/wiki/File:Soccer_ball.svg http://weelookang.blogspot.sg/2013/12/ejss-free-fall-model.htmlFor Teachers
Teacher-Submitted Activities
Share an activity! email Translations
Credits
|
About
TopicsKinematicsSpeed, velocity and acceleration Graphical analysis of motion Free-fall Effect of air resistance DescriptionThis simulation has a drop-down menu for exploration of(ii) moving with uniform velocity, use of progressive mathematical model is encouraged (iii) moving with non-uniform velocity (eg, constant acceleration) use of progressive mathematical model is encouraged When only the velocity-time graph check-box is selected, it can be explored for the following cases too. (ii) moving with uniform velocity (eg, no acceleration) model of the form Y = Y0+u*t (iii) moving with uniform acceleration (eg, constant acceleration = 9.81 m/s^2) model of the form Y = Y0+u*t+0.5*g*t (iv) moving with non-uniform acceleration (eg, with small ot large drag force acting thus acceleration changes). The default acceleration is set at-9.81 m/s^2 which is near to the Earth is constant and is approximately 10 m/s 2. Lastly, by selecting the 3 options of "free fall" "free_fall_with_small_air_resistance" "free_fall_with_large_air_resistance" It can provide the experience and evidences for describing the motion of bodies with constant weight falling with (large and small) or without air resistance, including reference to terminal velocity, a constant velocity as a result of balanced forces of weight of mass and the drag force giving rise to zero acceleration. Sample Learning Goals
(e) plot and interpret a displacement-time graph and a velocity-time
graph
(f) deduce from the shape of a displacement-time graph when a body is: (ii) moving with uniform velocity (iii) moving with non-uniform velocity (g) deduce from the shape of a velocity-time graph when a body is: (ii) moving with uniform velocity (iii) moving with uniform acceleration (iv) moving with non-uniform acceleration (i) state that the acceleration of free fall for a body near to the Earth is constant and is approximately 10 m/s 2 (j) describe the motion of bodies with constant weight falling with or without air resistance, including reference to terminal velocity Version:Translations
Credits
|
||||||||||||||||||||||||||||||||||||||||
Frequently Asked Questions About Free Fall and Kinematics Simulations
- What is the main focus of the provided simulations?
- These simulations primarily focus on exploring kinematics, specifically motion in the vertical (Y) direction, which includes free fall. They allow users to investigate concepts like speed, velocity, acceleration, and the effect of air resistance on falling objects. The simulations are designed to help understand the relationships between displacement, velocity, and time through graphical analysis.
- What types of motion can be modeled using these simulations?
- The simulations can model various types of motion, including:
- Objects at rest.
- Objects moving with uniform velocity (constant speed and direction).
- Objects moving with non-uniform velocity, particularly constant acceleration (e.g., free fall due to gravity).
- Objects experiencing non-uniform acceleration due to factors like air resistance, where the drag force is considered.
- How do these simulations handle air resistance?
- The simulations offer options to explore free fall under three conditions: no air resistance, small air resistance, and large air resistance. By selecting these options, users can see how air resistance affects an object's motion, particularly its acceleration and terminal velocity. When the drag force balances the weight of the object, terminal velocity is reached and acceleration becomes zero, leading to a constant downward velocity.
- What are some learning goals that these simulations aim to achieve?
- The primary learning goals include:
- Plotting and interpreting displacement-time and velocity-time graphs.
- Deducing motion characteristics (at rest, uniform velocity, non-uniform velocity) from the shapes of these graphs.
- Understanding that the acceleration due to gravity near the Earth is approximately constant at 9.81 m/s² (often rounded to 10 m/s²).
- Describing the motion of bodies falling with or without air resistance, including the concept of terminal velocity.
- What mathematical models are utilized in the simulations?
The simulations use mathematical models to describe the motion of objects. For constant velocity, the model is of the form Y = Y0 + u*t, where Y is the position, Y0 is the initial position, u is the velocity, and t is time. For uniform acceleration (constant acceleration, like free fall), the model is of the form Y = Y0 + u*t + 0.5*g*t² where g is the acceleration due to gravity. The simulations also illustrate how these models are adjusted to include air resistance, which introduces a changing acceleration.
- How can the simulations be used to analyze real-world scenarios?
- The simulations can be used to understand the real-world behavior of falling objects, for example:
- Analyzing the motion of a skydiver, including the time it takes to reach maximum height when thrown up and then fall back down.
- Predicting the position and velocity of a ball thrown vertically upwards.
- Comparing the falling behavior of objects with and without air resistance.
- Understanding the concept of terminal velocity.
- What types of data can be extracted or observed from the simulations?
The simulations can be used to observe and analyze: * Displacement of an object over time. * Velocity of an object over time. * Acceleration of an object, particularly how it changes with different forces. * The graphical relationship between displacement, velocity, and time. * Terminal velocity.
- Are there any resources provided to support learning with these simulations?
- Yes, the provided resources include:
- Sample worksheets that can be used for student activities
- A plethora of blog posts detailing other scenarios and physics concepts such as projectile motion, collisions, and gravity which can be used to deepen understanding
- Sample exercises such as the two sky divers falling from a helicopter with varying initial starts to conceptualize position and velocity
- Links to other interactive physics simulations and projects by the same authors.
- Details
- Parent Category: 03 Motion & Forces
- Category: 01 Kinematics
- Hits: 9994









.png
)


