🚂Student Learning Space Momentum vs Time Collision Carts JavaScript HTML5 Applet Simulation Model

Breadcrumbs

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.; Lye Sze Yee

Briefing Document: Momentum and Collisions Simulation

1. Overview

This document provides a summary of the "Student Learning Space Momentum vs Time Collision Carts JavaScript HTML5 Applet Simulation Model" found within the Open Educational Resources / Open Source Physics @ Singapore platform. The simulation is an interactive tool designed to help students understand the principles of momentum conservation during collisions. It's an HTML5 applet, making it accessible on various devices without needing specific software installations.

2. Main Themes and Concepts

The core themes explored by the simulation revolve around the following physics principles:

Momentum: The simulation introduces the concept of momentum as a vector quantity defined as the product of mass and velocity (p = mv).
Conservation of Linear Momentum: This is the central concept, which states: "The total momentum of a system remains constant provided that no external resultant force acts on the system." The simulation aims to demonstrate this principle in the context of collisions, showing how the total momentum before a collision equals the total momentum after the collision. The simulation visualizes this principle mathematically as: m1.u1 + m2.u2 = m1.v1 + m2.v2 Where:
m1, m2 represent the masses of the two colliding objects.
u1, u2 represent their initial velocities.
v1, v2 represent their final velocities.
Types of Collisions: The simulation explores different types of collisions, including:
Elastic Collisions: Collisions where both momentum and kinetic energy are conserved. The simulation allows the user to observe these conservation relationships in a "Perfectly elastic collision".
Inelastic Collisions: Collisions where momentum is conserved, but kinetic energy is not. Kinetic energy is lost in the collision, often converted to heat, sound, or deformation.
Completely Inelastic Collisions: A specific type of inelastic collision where the colliding objects stick together after the collision and move as one.
Kinetic Energy: The simulation also incorporates the concept of kinetic energy and allows users to observe changes in kinetic energy before and after collisions. The kinetic energy of a body is mathematically stated by the equation KE1 = ½ m1.v12.

3. Key Features of the Simulation

Interactive Sliders: The simulation uses interactive sliders that allow students to manipulate various parameters, such as the mass and initial velocity of each cart. These sliders enable students to "Explore the sliders allows varying the variables".
Dropdown Menu: Users can select what kind of collision is being simulated - elastic, inelastic, or completely inelastic via the dropdown menu.
Visualization: The simulation offers the ability to "show: velocity, for visualizing the velocity vector" and also allows users to "plot momentum vs time graph, for different representation of data for momentum of cart 1, 2 and both." Similarly, users can "plot kinetic energy vs time graph, for different representation of data for kinetic energy of cart 1, 2 and both".
Hints: The simulation includes hints: "hint: COM, for the equation of conservation of momentum" and "hint: COKE, or the equation of conservation of kinetic energy". These provide useful reminders to the user as they explore the simulation.
Frictionless Environment: The simulation is set in an environment where friction is ignored, allowing students to focus on the core physics principles without the added complication of friction forces. The simulation takes place on "frictionless floor and wheels".

4. Pedagogical Approach and Learning Objectives

The simulation is designed as an educational tool, aiming to achieve the following:

Interactive Learning: By allowing students to actively manipulate the variables, the simulation promotes hands-on learning and deeper understanding of the physics concepts.
Visual Representation: The simulation provides clear visual representations of the collision, as well as graphs of the momentum and kinetic energy. This helps students relate the mathematical formulas to physical events.
Conceptual Understanding: The main goal is for students to understand the conservation of momentum during different types of collisions and how kinetic energy behaves.
Data Interpretation: Plotting options further helps with analyzing how the momentum and kinetic energy of each cart changes over time.

5. Technical Aspects

Technology: The model is a "JavaScript HTML5 Applet Simulation Model", ensuring broad compatibility and easy accessibility on web browsers.
Development Tool: The simulation was created using "Easy Java Simulations (EJS) version 5.2 authoring and modeling tool". The source code is also modifiable via EJS, provided EJS is installed on the user's computer. The source mentions that you can examine and modify this compiled EJS model if you "run the model (double click on the model's jar file), right-click within a plot, and select "Open EJS Model" from the pop-up menu."
Accessibility: The simulation is available as a web embed and as apps available for both Google Play and iOS.

6. Related Resources and Materials

The platform provides numerous resources, including:

Worksheets: A variety of worksheets with sample problems for different school levels, including junior college. Examples include:
"Momentum1D01momAJCPBI Worksheet_Dynamics_2012_final.docx"
"Momentum1D01momIJCMomentum_worksheet_v1.6_lab_worksheet_IJC1.doc"
Videos: Links to related videos, including a Facebook video and two videos made by the model's creator, are available. Example:
"Astro Academy: Principia - Collisions by National Space Academy"
External Simulations: Links to similar simulations from other sources such as Walter Fendt, Physicsclassroom, and PhET are also provided.

7. Educational Context

The simulation is part of a larger collection of open educational resources aimed at promoting interactive learning in physics, particularly in the area of dynamics. Its inclusion in the "Student Learning Space" indicates its intended use in a formal educational setting.

8. Conclusion

The "Student Learning Space Momentum vs Time Collision Carts JavaScript HTML5 Applet Simulation Model" is a valuable tool for teaching the principles of momentum and collisions. It utilizes interactive features and visualizations to promote a deeper understanding of the underlying physics, with the capacity to further be explored using the associated worksheets and videos. Its accessibility as an HTML5 applet makes it a versatile resource for students and educators alike.

Frequently Asked Questions: Momentum and Collisions

What is momentum, and how is it calculated? Momentum is a measure of a moving object's mass and velocity. It is a vector quantity represented by the symbol 'p'. The formula to calculate momentum is: p = m * v, where 'm' is the mass of the object and 'v' is its velocity. The direction of the momentum is the same as the direction of the velocity.
What is the principle of conservation of linear momentum, and under what conditions does it apply? The principle of conservation of linear momentum states that the total momentum of a system remains constant if there are no net external forces acting on that system. This means that in a closed system, like a collision between two carts on a frictionless surface, the total momentum before the collision is equal to the total momentum after the collision. Mathematically, for two colliding bodies, this is expressed as: m1u1 + m2u2 = m1v1 + m2v2, where m1 and m2 are the masses, u1 and u2 are the initial velocities, and v1 and v2 are the final velocities of the two objects. This principle is applicable as long as external forces like friction are negligible.
How are collisions classified, and what are the key differences between them? Collisions are classified into three main types: elastic, inelastic, and completely inelastic.

Elastic Collisions: In a perfectly elastic collision, both momentum and kinetic energy are conserved. This means that the total kinetic energy of the system before the collision is equal to the total kinetic energy after the collision.
Inelastic Collisions: In an inelastic collision, momentum is conserved, but kinetic energy is not. Some kinetic energy is lost, usually converted into other forms of energy like heat or sound.
Completely Inelastic Collisions: In a completely inelastic collision, momentum is conserved, but the colliding objects stick together after the collision and the system experiences the greatest loss of kinetic energy.

What is kinetic energy, and how does it relate to collisions? Kinetic energy is the energy an object possesses due to its motion. It is calculated using the formula KE = 1/2 * m * v², where 'm' is the mass and 'v' is the velocity of the object. In collisions, kinetic energy is either conserved (as in perfectly elastic collisions) or not conserved (as in inelastic and completely inelastic collisions). The change in kinetic energy is often a key factor in understanding the nature of the collision.
How can a simulation model help in understanding momentum and collisions? A simulation model like the "Student Learning Space Momentum vs Time Collision Carts JavaScript HTML5 Applet Simulation Model" allows users to explore and visualize the concepts of momentum and collisions in a dynamic and interactive way. Users can change variables like masses and initial velocities of carts, select collision types (elastic, inelastic), and see the effects on momentum and kinetic energy through graphs and visual representations. This hands-on approach enhances conceptual understanding and makes learning more engaging. The simulations also provide hints of the relevant equations such as conservation of momentum and kinetic energy.
What parameters can be adjusted in the collision simulation, and what do they represent? In the collision simulation, you can adjust the following parameters:

Mass of Cart One (m1): The mass of the first cart, measured in kilograms (kg).
Initial Velocity of Cart One (u1): The initial velocity of the first cart, measured in meters per second (m/s).
Mass of Cart Two (m2): The mass of the second cart, measured in kilograms (kg).
Initial Velocity of Cart Two (u2): The initial velocity of the second cart, measured in meters per second (m/s). These parameters allow you to set up different collision scenarios and observe how these variable affect momentum and kinetic energy.

What visualizations and data representations does the simulation provide to understand collisions? The simulation provides various ways to visualize and understand collisions:

Velocity vectors: Displaying arrows to represent the direction and magnitude of the carts' velocities.
Momentum vs. Time graphs: Visual representations of how momentum changes for each cart and the total system over time.
Kinetic Energy vs Time graphs: Visual representations of how kinetic energy changes for each cart and the total system over time. These visualizations help to make the abstract concepts of momentum, kinetic energy, and their conservation more tangible.

What external resources are available for further learning about collisions and momentum? The resource page provides various external links and materials for further learning. These include:

Other interactive simulations: Like the Collision Carts by Walter Fendt, Collision Carts by Physicsclassroom, and Collision Lab by PhET.
Educational Videos: Including "Astro Academy: Principia - Collisions by National Space Academy" and EJS applet videos demonstrating elastic and inelastic collisions.
Worksheets and Documents: Various teacher and student resources that include exercises and explanations.
Open Source Physics (OSP) resources: For understanding computational models and the tools used to create the simulation. These resources provide additional opportunities to explore the topic in more detail and from different perspectives.

Apps

https://play.google.com/store/apps/details?id=com.ionicframework.collisioncartapp170147

https://itunes.apple.com/us/app/collision-carts-simulator/id1177377945?mt=8

Description

Momentum One Dimension Collision Model

The motion of a body of mass m and velocity v is described by a vector quantity known as momentum p where

p = m v

When objects collide, whether trains, cars, billiard balls, shopping carts, or your foot and the sidewalk, the results can be complicated. Yet even in the most chaotic of collisions, as long as there are no net external forces acting on the colliding objects, one principle always holds and provides an excellent tool for understanding the collision. That principle is called the conservation of linear momentum which states that

The total momentum of a system remains constant provided that no external resultant force acts on the system

For two bodies colliding linearly, it is written mathematically as a vector equation

Total initial momentum = total final momentum

m₁.u₁ + m₂.u₂ = m₁.v₁ + m₂.v₂

If external forces (such as friction) are ignored, the total momentum of two carts prior to a collision (left side of equation) is the same as the total momentum of the carts after the collision (right side of equation).

Collisions are classified into elastic (or perfectly elastic), inelastic and completely inelastic.

There is also a concept of kinetic energy of a moving body is stated mathematically by the following equation:

KE1 = ½ m₁.v₁²

Main Simulation View
The simulation has 2 collision carts on frictionless floor and wheels.
Sliders

Explore the sliders allows varying the variables .

   * mass of cart ONE, mass_1, m₁ in kg
   * initial velocity of cart ONE, u₁ in m/s
   * mass of cart TWO, mass_2, m₂ in kg
   * initial velocity of cart TWO, u₂ in m/s

DropDown Menu
Allows for selecting what kind of collision is simulated.

A Perfectly elastic collision is defined as one in which both conservation of momentum and conservation of kinetic energy are observed
A Perfectly Inelastic collision is defined as one in which conservation of momentum is observed but the colliding carts stick together after collision with kinetic energy loss

DropDown Menu
show: velocity, for visualizing the velocity vector
plot momentum vs time graph, for different representation of data for momentum of cart 1, 2 and both.
plot kinetic energy vs time graph, for different representation of data for kinetic energy of cart 1, 2 and both.
hint: COM, for the equation of conservation of momentum
hint: COKE, or the equation of conservation of kinetic energy

Buttons
Play
Step Forward
Reset
have their usual meaning.

Credits:
The Momentum 1D JavaScript Collision model was created by created by lookang using the Easy Java Simulations (EJS) version 5.2 authoring and modeling tool. Shout our thanks to the Ejs community namely, Francisco Esquembre, Félix J. García Clemente , Fu-Kwun Hwang and Wolfgang Christian for their professional learning community support. You can examine and modify this compiled EJS model if you run the model (double click on the model's jar file), right-click within a plot, and select "Open EJS Model" from the pop-up menu. You must, of course, have EJS installed on your computer. Information about EJS is available at: http://www.um.es/fem/Ejs/ and in the OSP comPADRE collection http://www.compadre.org/OSP/.

Video

Astro Academy: Principia - Collisions by National Space Academy

Ejs open source java applet 1D collision carts Elastic and Inelastic Collision by lookang lawrence wee

Ejs open source java applet 1D collision carts Elastic and Inelastic Collision v2 by lookang lawrence wee

https://www.facebook.com/AskMencom/videos/10153205007388723/

Screenshots

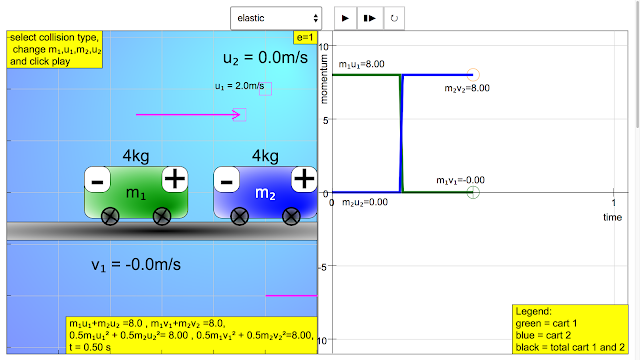Student Learning Space Momentum vs Time Collision Carts JavaScript HTML5 Applet Simulation Model
Elastic collision, notice momentum is conserved
Total initial momentum = total final momentum
m1.u1 + m2.u2 = m1.v1 + m2.v2
(4)(2)+ (4)(0) = 4(0)+ 4(2)
https://sg.iwant2study.org/ospsgx/index.php/587

Worksheets

Versions

http://weelookang.blogspot.sg/2013/09/one-dimension-collision-js-model.html JavaScript version of EJSS One Dimension Collision JS Model by
http://weelookang.blogspot.sg/2012/02/ejs-open-source-collision-carts-model.html Java version of the Ejs Open Source Collision Carts Model with AJC and RVHS
http://iwant2study.org/lookangejss/02_newtonianmechanics_3dynamics/ejs/ejs_model_Momentum1DForceModel09.jar Java version of simulation on Digital Library

Research

arXiv:1204.4964 [pdf, other]

One-dimensional collision carts computer model and its design ideas for productive experiential learning

Loo Kang Wee

Comments: 6 pages, 8 figures, 1 table, 1 L. K. Wee, Physics Education 47 (3), 301 (2012); ISSN 0031-9120

Journal-ref: Physics Education, 47(3), 301 (2012)

Subjects: Physics Education (physics.ed-ph); Classical Physics (physics.class-ph); Computational Physics (physics.comp-ph)

Other Resources

http://www.walter-fendt.de/html5/phen/collision_en.htm Collision Carts by Walter Fendt
http://www.physicsclassroom.com/Physics-Interactives/Momentum-and-Collisions/Collision-Carts Collision Carts by Physicsclassroom
http://weelookang.blogspot.sg/2014/11/ejss-collision-model-by-dave-lommen.html EJSS collision model by Dave Lommen
http://weelookang.blogspot.sg/2014/07/ejs-1d-collision-model-with-virtual.html EJS 1D collision model with virtual spring model by Fu-Kwun Hwang and Loo Kang Wee
https://phet.colorado.edu/en/simulation/collision-lab Collision Lab by PhET
http://www.mrmont.com/games/carcollision.html
http://www.opensourcephysics.org/items/detail.cfm?ID=14162 International Space Station: Collisions Video Analysis with Tracker by Tim Peake, Robin Mobbs, Anu Ojha, Andy McMurry, and Sophie Allan
https://www.geogebra.org/m/n3X5njnT Elastic & Inelastic Collisions by ukukuku
https://www.geogebra.org/m/gSmRe62s The Ballistic Pendulum by ukukuku
https://www.geogebra.org/m/Ks939X8m Conservation of Momentum and Energy by ukukuku

Frequently Asked Questions: Momentum and Collisions

What is momentum, and how is it calculated? Momentum is a measure of a moving object's mass and velocity. It is a vector quantity represented by the symbol 'p'. The formula to calculate momentum is: p = m * v, where 'm' is the mass of the object and 'v' is its velocity. The direction of the momentum is the same as the direction of the velocity.
What is the principle of conservation of linear momentum, and under what conditions does it apply? The principle of conservation of linear momentum states that the total momentum of a system remains constant if there are no net external forces acting on that system. This means that in a closed system, like a collision between two carts on a frictionless surface, the total momentum before the collision is equal to the total momentum after the collision. Mathematically, for two colliding bodies, this is expressed as: m1u1 + m2u2 = m1v1 + m2v2, where m1 and m2 are the masses, u1 and u2 are the initial velocities, and v1 and v2 are the final velocities of the two objects. This principle is applicable as long as external forces like friction are negligible.
How are collisions classified, and what are the key differences between them? Collisions are classified into three main types: elastic, inelastic, and completely inelastic.

Elastic Collisions: In a perfectly elastic collision, both momentum and kinetic energy are conserved. This means that the total kinetic energy of the system before the collision is equal to the total kinetic energy after the collision.
Inelastic Collisions: In an inelastic collision, momentum is conserved, but kinetic energy is not. Some kinetic energy is lost, usually converted into other forms of energy like heat or sound.
Completely Inelastic Collisions: In a completely inelastic collision, momentum is conserved, but the colliding objects stick together after the collision and the system experiences the greatest loss of kinetic energy.

What is kinetic energy, and how does it relate to collisions? Kinetic energy is the energy an object possesses due to its motion. It is calculated using the formula KE = 1/2 * m * v², where 'm' is the mass and 'v' is the velocity of the object. In collisions, kinetic energy is either conserved (as in perfectly elastic collisions) or not conserved (as in inelastic and completely inelastic collisions). The change in kinetic energy is often a key factor in understanding the nature of the collision.
How can a simulation model help in understanding momentum and collisions? A simulation model like the "Student Learning Space Momentum vs Time Collision Carts JavaScript HTML5 Applet Simulation Model" allows users to explore and visualize the concepts of momentum and collisions in a dynamic and interactive way. Users can change variables like masses and initial velocities of carts, select collision types (elastic, inelastic), and see the effects on momentum and kinetic energy through graphs and visual representations. This hands-on approach enhances conceptual understanding and makes learning more engaging. The simulations also provide hints of the relevant equations such as conservation of momentum and kinetic energy.
What parameters can be adjusted in the collision simulation, and what do they represent? In the collision simulation, you can adjust the following parameters:

Mass of Cart One (m1): The mass of the first cart, measured in kilograms (kg).
Initial Velocity of Cart One (u1): The initial velocity of the first cart, measured in meters per second (m/s).
Mass of Cart Two (m2): The mass of the second cart, measured in kilograms (kg).
Initial Velocity of Cart Two (u2): The initial velocity of the second cart, measured in meters per second (m/s). These parameters allow you to set up different collision scenarios and observe how these variable affect momentum and kinetic energy.

What visualizations and data representations does the simulation provide to understand collisions? The simulation provides various ways to visualize and understand collisions:

Velocity vectors: Displaying arrows to represent the direction and magnitude of the carts' velocities.
Momentum vs. Time graphs: Visual representations of how momentum changes for each cart and the total system over time.
Kinetic Energy vs Time graphs: Visual representations of how kinetic energy changes for each cart and the total system over time. These visualizations help to make the abstract concepts of momentum, kinetic energy, and their conservation more tangible.

What external resources are available for further learning about collisions and momentum? The resource page provides various external links and materials for further learning. These include:

Other interactive simulations: Like the Collision Carts by Walter Fendt, Collision Carts by Physicsclassroom, and Collision Lab by PhET.
Educational Videos: Including "Astro Academy: Principia - Collisions by National Space Academy" and EJS applet videos demonstrating elastic and inelastic collisions.
Worksheets and Documents: Various teacher and student resources that include exercises and explanations.
Open Source Physics (OSP) resources: For understanding computational models and the tools used to create the simulation. These resources provide additional opportunities to explore the topic in more detail and from different perspectives.

5 1 1 1 1 1 1 1 1 1 1 Rating 5.00 (1 Vote)

Details: Written by Fremont; Parent Category: 03 Motion & Forces; Category: 02 Dynamics; Published: 29 April 2018; Created: 30 April 2018; Last Updated: 14 February 2025; Hits: 10973