About
Topics
KinematicsSpeed, velocity and acceleration
Graphical analysis of motion
Description
This simulation has a drop-down menu for exploration of(i) at rest use of progressive mathematical model is encouraged X = 0 for example
(ii) moving with uniform velocity, use of progressive mathematical model is encouraged for example X = 1*t for a constant velocity motion of v =1 m/s
(iii) moving with non-uniform velocity (eg, constant acceleration) use of progressive mathematical model is encouraged for example X = 0.5*1*t^2 for a constant acceleration motion of a =1 m/s^2
When only the velocity-time graph check-box is selected, it can be explored for the following cases too.
(i) at rest ,
(ii) moving with uniform velocity (eg, no acceleration)
(iii) moving with uniform acceleration (eg, constant acceleration = 9.81 m/s^2)
Sample Learning Goals
(f) deduce from the shape of a displacement-time graph when a body is:
(i) at rest example of progressive mathematical model is encouraged X = 0
(ii) moving with uniform velocity example of progressive mathematical model is encouraged X = 1*t for a constant velocity motion of v =1 m/s
(iii) moving with non-uniform velocity example of X = 0.5*1*t^2 for a constant acceleration motion of a =1 m/s^2
(g) deduce from the shape of a velocity-time graph when a body is:
(i) at rest
(ii) moving with uniform velocity
(iii) moving with uniform acceleration
(iv) moving with non-uniform acceleration
Version:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits
 This email address is being protected from spambots. You need JavaScript enabled to view it.
This email address is being protected from spambots. You need JavaScript enabled to view it.
Briefing Document: Primary Kinematics 1D Simulation Model
1. Overview
This document reviews a physics simulation model focused on 1D kinematics (motion in a straight line), specifically designed using JavaScript and HTML5. The model is an open educational resource (OER) developed by the Open Educational Resources / Open Source Physics @ Singapore initiative. It aims to help students understand the relationships between displacement, velocity, and acceleration through interactive visualizations and mathematical modeling. The model is available as an embeddable applet.
2. Main Themes & Key Ideas
- Kinematics Fundamentals: The primary focus of the simulation is to explore basic kinematic concepts:
- Displacement: Represented by the variable 'X', it is used to model the position of the car.
- Velocity: The rate of change of displacement, both uniform (constant) and non-uniform (changing).
- Acceleration: The rate of change of velocity, primarily constant acceleration is explored.
- Mathematical Modeling: The simulation encourages students to use progressive mathematical models to describe motion. Examples given include:
- Rest: X = 0 (position does not change)
- Uniform Velocity: X = 1*t (where the velocity is a constant 1 m/s)
- Uniform Acceleration: X = 0.51t^2 (where the acceleration is a constant 1 m/s²)
- These models allow students to observe how mathematical equations connect to physical motions.
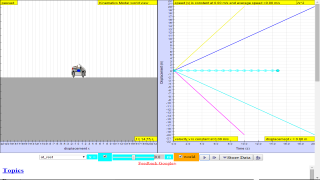
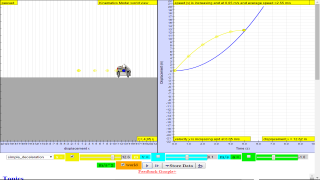
- Graphical Analysis: A key learning goal is the interpretation of displacement-time and velocity-time graphs. Students should deduce the state of motion from the shape of these graphs:
- Displacement-time graphs:Horizontal line: At rest.
- Straight diagonal line: Uniform velocity.
- Curved line: Non-uniform velocity (e.g., acceleration).
- Velocity-time graphs:Horizontal line at y=0: At rest.
- Horizontal line (not at y=0): Uniform velocity.
- Straight diagonal line: Uniform acceleration.
- Curved line: Non-uniform acceleration.
- Interactive Learning: The simulation is an interactive tool designed for use on various platforms including computers, tablets and phones. This aims to enhance student engagement and understanding.
- Open Educational Resource: The simulation is freely available for use and modification under the Creative Commons Attribution-Share Alike 4.0 Singapore License. This means that the resource can be shared, adapted, and reused for educational purposes, fostering collaboration and accessibility.
- Pedagogical Approach:
- Mystery Approach: The simulation is framed as a challenge, where students are tasked to find a "predictive equation that can be used to tell the future" about the car's motion. This approach is intended to generate curiosity.
- Little Professor/Little Teachers: The document suggests using learning management systems (e.g., Edmodo, WhatsApp) to encourage student interaction and peer teaching.
3. Important Facts and Ideas
- Simulation Capabilities: The model allows students to explore different scenarios of motion by choosing from a drop-down menu:
- At rest
- Moving with uniform velocity
- Moving with non-uniform velocity (constant acceleration)
- Exploring cases of motion from graphs of velocity-time.
- Learning Goals: Key student learning objectives include:
- "plot and interpret a displacement-time graph and a velocity-time graph"
- "deduce from the shape of a displacement-time graph when a body is: (i) at rest (ii) moving with uniform velocity (iii) moving with non-uniform velocity"
- "deduce from the shape of a velocity-time graph when a body is: (i) at rest (ii) moving with uniform velocity (iii) moving with uniform acceleration (iv) moving with non-uniform acceleration"
- Technical Details: The simulation uses the Easy JavaScript Simulation (EJS) framework. Different versions of the EJS software are mentioned, indicating a potential for bugs if not using the correct version (EJS_5.1_150302 is suggested).
- The simulation provides embed codes to easily incorporate into web pages.
- Supporting Materials: Worksheets, videos, and pedagogical write-ups are available. These supplemental materials aim to support the simulation's use in the classroom. Links to external resources such as The Physics Classroom and The Physics Aviary are also provided as sources of similar learning tools.
- The simulation is part of a larger project, "Understanding Teacher Learning Community as Support for Implementation of Open Source Physics for Conceptual Instruction," indicating its integration within a broader educational initiative.
4. Quotes & Key Phrases:
- "This simulation has a drop-down menu for exploration of (i) at rest (ii) moving with uniform velocity, (iii) moving with non-uniform velocity (eg, constant acceleration)" - Describing the available modes of the simulation
- "use of progressive mathematical model is encouraged" - Highlighting the approach of linking mathematical models to the observed motion.
- "Give the challenge to solve the mystery of a predictive equation that can be use to tell the future, more precisely the movement of a car, in a physics lesson." - Describing the mystery approach.
5. Related Resources
The document also links to a wide array of other resources available on the Open Educational Resources / Open Source Physics @ Singapore site, including simulations on various topics (e.g., gravity, energy, waves, optics, collisions), interactive activities using Tracker video analysis, and authoring tools like Easy JavaScript Simulation.
6. Conclusion
The "Primary Kinematics or Moving Car 1D JavaScript HTML5 Applet Simulation Model" is a valuable tool for teaching fundamental kinematics concepts. It combines visual and interactive elements with a focus on mathematical modeling and graph interpretation. The open-source nature of the resource, alongside supporting materials and pedagogical frameworks, makes it a flexible and adaptable tool for educators. This single source document is part of a larger and well-developed set of physics education resources.
Kinematics Simulation Study Guide
Quiz
Answer each question in 2-3 sentences.
- What are the three primary motion scenarios that the kinematics simulation allows users to explore?
- How can you use the simulation to understand the concept of uniform velocity?
- What mathematical model is suggested to describe an object moving with constant acceleration in the simulation?
- Besides displacement-time graphs, what other type of graph can be generated by the simulation?
- How can a velocity-time graph be used to deduce when a body is at rest?
- What is meant by "progressive mathematical model" in the context of the simulation?
- According to the source material, what is the role of a "mystery" within the pedagogical approach?
- What are some of the learning management systems suggested to arouse and sustain interest in the lesson?
- Why is it valuable to understand a student's prior knowledge when introducing physics concepts?
- What types of devices can the simulation be used on?
Quiz Answer Key
- The simulation explores motion scenarios of an object at rest, moving with uniform velocity, and moving with non-uniform velocity (constant acceleration). It uses these basic scenarios to explore more complex motion.
- The simulation allows you to model uniform velocity by inputting equations like X=1*t, and it presents a graphical representation of the motion (position vs time), showing a straight line with constant slope. This visualization helps solidify the concept of constant velocity.
- The simulation recommends using a mathematical model such as X = 0.51t^2 to describe motion with constant acceleration. This model shows how displacement changes in relation to the square of the time.
- In addition to displacement-time graphs, the simulation can generate velocity-time graphs. These graphs allow the user to visualize changes in velocity over time, providing insights into acceleration and motion.
- On a velocity-time graph, a horizontal line at a velocity of zero indicates that a body is at rest. This means that there is no change in position over time.
- A "progressive mathematical model" refers to a sequence of models introduced in the learning process. Beginning with the simplest model (X=0, for example), students are encouraged to progress towards more complex models such as X = 1t (uniform motion) or X = 0.51*t^2 (uniform acceleration).
- In the pedagogical approach, a "mystery" is presented in the form of a predictive equation that can tell the future movement of an object. Solving this mystery helps students engage with the material and serves as a diagnostic tool for the teacher.
- The lesson plan suggests existing school learning management systems like Edmodo and Whatsapp groups to arouse and sustain interest. These tools allow for easy communication and collaborative learning.
- Understanding a student’s prior knowledge is important because it allows the teacher to identify knowledge gaps and provide personalized mentoring to help the students' learning. This makes learning more effective and focused.
- The simulation is accessible on a wide variety of devices such as Android/iOS phones/tablets/iPads, as well as Windows/MacOSX/Linux laptops/desktops, and Chromebook laptops. This allows flexible access for a range of learners.
Essay Questions
Answer each question in essay format (multiple paragraphs).
- Discuss how the use of mathematical models in the kinematics simulation can enhance a student's understanding of motion concepts.
- Explain how the kinematics simulation supports the understanding of different types of motion: at rest, uniform velocity, and non-uniform velocity.
- Describe the pedagogical approach suggested for using the simulation. How does this approach encourage student engagement and learning?
- Analyze how the visualization of displacement-time and velocity-time graphs contribute to a deeper understanding of kinematic principles.
- Reflect on the potential impact of this type of interactive simulation on the future of physics education. Consider the benefits and challenges of incorporating such technologies.
Glossary of Key Terms
Kinematics: The branch of mechanics that describes the motion of objects without considering the causes of the motion.
Uniform Velocity: Motion at a constant speed in a straight line. This means both the speed and direction are not changing.
Non-uniform Velocity: Motion where the velocity is changing over time, either in speed or direction, or both. Acceleration is present.
Constant Acceleration: Motion where the rate of change of velocity is constant.
Displacement-time Graph: A graph that plots the position of an object against time. The slope of the line represents the velocity.
Velocity-time Graph: A graph that plots the velocity of an object against time. The slope of the line represents the acceleration.
Progressive Mathematical Model: A series of increasingly complex mathematical equations introduced to represent different scenarios of motion, typically from very simple to more complex.
Open Educational Resource (OER): Educational materials that are freely available for anyone to use, adapt, and share.
Pedagogy: The method and practice of teaching, especially as an academic subject or theoretical concept.
Learning Management System (LMS): A software application for the administration, documentation, tracking, reporting, and delivery of educational courses, training programs, or learning and development programs. Examples include Edmodo.
Simulation: A computer-based model designed to represent a real-world system or phenomenon. In this case, a model of a moving object.
Worksheet
- Slides for Workshop Link1 , Link2
- Final version Link1, Link2 by Lyna, Gavin, Dave and lookang
- Motion in One Dimension student worksheet (dl-gwf) Link1, Link2 by Lyna, Gavin, Dave and lookang
Video
- https://youtu.be/ZYIeBKDBXU8 Kinematics 1d simulation video tutorial with modeling pedagogy by lookang lawrence wee
- https://youtu.be/SsSPd6I4BnA Kinematics 1D simulation running on hmtl5 Modeling pedagogy 2 by lookang lawrence wee
Pedagogical Writeup
| Process | Lesson Implementation | |
| Sub-Process(es) | Introducing the Lesson / Arousing and Sustaining Interest | |
| Teaching Action | Mystery | |
Technology:
mystery could take the form an describe it all equation, called model.
Give the challenge to solve the mystery of a predictive equation that can be use to tell the future, more precisely the movement of a car, in a physics lesson.
Through the model selected by the students, it gives an indication of the students prior knowledge about what they know now, so that the teacher can understand the gaps of understanding for personalised mentoring https://sg.iwant2study.org/ospsg/index.php/interactive-resources/physics/02-newtonian-mechanics/01-kinematics/38-kinematics-1d
| Process | Lesson Implementation | |
| Sub-Process(es) | Introducing the Lesson / Arousing and Sustaining Interest | |
| Teaching Action | Little Professor/Little Teachers | |
Technology:
use exisiting schools' learning management system such as https://www.edmodo.com/ or Whatapp group chat to allow of arousing and sustaining interest.
Other simulations
- http://www.physicsclassroom.com/Physics-Interactives/1-D-Kinematics/Graphs-and-Ramps
- http://www.thephysicsaviary.com/Physics/Programs/Labs/EquationsOfMotionLab/index.html
Project related:
Understanding Teacher Learning Community as Support for Implementation of Open Source Physics for Conceptual Instruction
Project Number: OER 10/15 GWF
Project Duration: 01 July 2015 - 30 April 2017
http://weelookang.blogspot.sg/2015/07/understanding-teacher-learning.html
Family of Resources
| Secondary | Junior College | ||||||||||
About
TopicsKinematicsSpeed, velocity and acceleration Graphical analysis of motion DescriptionThis simulation has a drop-down menu for exploration of(i) at rest use of progressive mathematical model is encouraged X = 0 for example (ii) moving with uniform velocity, use of progressive mathematical model is encouraged for example X = 1*t for a constant velocity motion of v =1 m/s (iii) moving with non-uniform velocity (eg, constant acceleration) use of progressive mathematical model is encouraged for example X = 0.5*1*t^2 for a constant acceleration motion of a =1 m/s^2 When only the velocity-time graph check-box is selected, it can be explored for the following cases too. (i) at rest , (ii) moving with uniform velocity (eg, no acceleration) (iii) moving with uniform acceleration (eg, constant acceleration = 9.81 m/s^2) Sample Learning Goals
(e) plot and interpret a displacement-time graph and a velocity-time
graph
(f) deduce from the shape of a displacement-time graph when a body is: (i) at rest example of progressive mathematical model is encouraged X = 0 (ii) moving with uniform velocity example of progressive mathematical model is encouraged X = 1*t for a constant velocity motion of v =1 m/s (iii) moving with non-uniform velocity example of X = 0.5*1*t^2 for a constant acceleration motion of a =1 m/s^2 (g) deduce from the shape of a velocity-time graph when a body is: (i) at rest (ii) moving with uniform velocity (iii) moving with uniform acceleration (iv) moving with non-uniform acceleration Version:Translations
Credits
|
|||||||||||
FAQ on Kinematics Simulations and Modeling
- What is the primary focus of the Kinematics 1D simulation model?
- This simulation primarily focuses on exploring one-dimensional motion, also known as primary kinematics. It allows users to investigate the movement of an object (represented by a car) under various conditions such as being at rest, moving with uniform velocity, and moving with non-uniform velocity (including constant acceleration). The simulation emphasizes a progressive approach to mathematical modeling of these movements.
- What are the key modes of motion that can be explored using the simulation?
- The simulation allows users to explore:
- An object at rest, where the position is modeled as X=0.
- Motion with uniform velocity, where position is modeled linearly with time such as X = 1*t
- Motion with non-uniform velocity (specifically constant acceleration), where position changes parabolically with time such as X=0.5 * 1*t^2. When using the velocity-time graph view, it can also be used to explore an object at rest, moving with uniform velocity (no acceleration), moving with uniform acceleration, and moving with non-uniform acceleration.
- How does the simulation encourage the use of mathematical models?
- The simulation encourages the use of progressive mathematical models to represent the different types of motion. For example, it suggests using X=0 for an object at rest, X=1t for uniform velocity, and X=0.51*t^2 for constant acceleration. By aligning the simulation with these mathematical models, users can see how equations directly translate to motion and create a stronger link between theory and practice.
- What are displacement-time graphs and velocity-time graphs and how can they be used?
- Displacement-time graphs and velocity-time graphs are visual tools for representing the motion of an object. Displacement-time graphs plot the position of an object over time, whereas the velocity-time graph shows how velocity changes over time. In this simulation, users can interpret the shape of these graphs to deduce whether an object is at rest, moving with uniform velocity, moving with uniform acceleration, or moving with non-uniform acceleration. Different slopes of lines on these graphs correspond to changes in velocity or acceleration respectively.
- What are some of the learning goals associated with using this kinematics simulation?
- The learning goals include: plotting and interpreting displacement-time graphs and velocity-time graphs, and deducing the state of motion of an object based on these graphs. Specifically, users should be able to determine when a body is at rest, moving with uniform velocity, or moving with non-uniform velocity or acceleration from the graphs.
- Besides the 1D kinematics simulation, what other types of simulations are available on the same platform?
- The platform hosts a wide array of physics simulations, ranging from basic mechanics (like projectile motion, collisions, and oscillations) to advanced topics like electromagnetism, optics, quantum physics, and thermodynamics. Other models available include those involving circuits, fields, forces, and energy, as well as Tracker simulations to analyse videos and create models. They range across all school levels from primary to junior college.
- What is the pedagogy used in this simulation?
- The pedagogy used in this simulation involves presenting a mystery, where users try to predict the movement of an object with a predictive mathematical equation. The simulation allows users to explore their prior knowledge through this model selection, and also aims to promote personalized learning via teacher mentoring, along with the use of learning platforms such as Edmodo or WhatsApp group chats to sustain interest in the content.
- What tools are used in the development of these simulations?
- The simulations are created using Easy JavaScript Simulation (EJS), which is an open-source tool that allows the design and creation of interactive physics simulations. They are designed to be embeddable in websites and compatible with various devices such as Windows, MacOSX, Linux, ChromeBook laptops, Android, and iOS tablets and phones, making these resources widely accessible.
- Details
- Parent Category: 03 Motion & Forces
- Category: 01 Kinematics
- Hits: 10305









.png
)


