Vector Addition, and Drawing Patterns

This simulation illustrates the tail-to-tip method of adding vectors.

The table at the bottom shows the components and lengths of the vectors.

You can also rotate the vectors and trace out some interesting patterns.

Activities

Given the magnitude and angles of the two vectors, do you agree with the values shown for the components of the three vectors in the table at the bottom? Explain how the components are determined.
For a given pair of vectors, how do you find the maximum possible magnitude of their resultant vector? How do you determine the minimum possible magnitude?
By changing the orientation of one or both of the vectors, can you obtain a resultant vector with any magnitude between the minimum and maximum value
Adjust the lengths of the two vectors and their rotation rates, and then hit Play. See what kind of interesting patterns you can make, just by adding vectors.

Translations

Code	Language		Translator	Run

Credits

Andrew Duffy; Loo Kang Wee

Main Theme:

The central theme across both sources is the use of an interactive computer simulation to enhance the understanding of vector addition and to demonstrate the visually interesting patterns that can be created by the resultant of two rotating vectors. This approach emphasizes hands-on learning and the exploration of mathematical concepts through visual and dynamic means.

Most Important Ideas and Facts:

Tail-to-Tip Vector Addition: The simulation specifically illustrates the fundamental "tail-to-tip" method of adding vectors. The "About" section explicitly states: "This simulation illustrates the tail-to-tip method of adding vectors." This is a core concept in vector mathematics.
Vector Components and Magnitudes: The simulation provides a table displaying the components and lengths (magnitudes) of the individual vectors and their resultant. This allows users to quantitatively analyze the effects of vector addition. The "About" section mentions: "The table at the bottom shows the components and lengths of the vectors." Activity 1 directly encourages users to verify the calculated components based on the given magnitudes and angles.
Exploration of Resultant Vector Properties: The simulation facilitates the investigation of the resultant vector's properties. Activity 2 prompts users to consider: "For a given pair of vectors, how do you find the maximum possible magnitude of their resultant vector? How do you determine the minimum possible magnitude?" This encourages understanding of how the relative orientation of vectors affects the magnitude of their sum. Activity 3 further explores the range of possible resultant vector magnitudes: "By changing the orientation of one or both of the vectors, can you obtain a resultant vector with any magnitude between the minimum and maximum value?"
Creative Pattern Generation: A key and novel aspect of this simulation is the ability to generate "interesting patterns" by adjusting the lengths and "rotation rates" (angular velocities) of the two vectors and then observing the trace of their resultant. The "About" section highlights this: "You can also rotate the vectors and trace out some interesting patterns." Activity 4 explicitly guides this exploration: "Adjust the lengths of the two vectors and their rotation rates, and then hit Play. See what kind of interesting patterns you can make, just by adding vectors."
Examples of Emergent Patterns: The "For Teachers" section provides concrete examples of patterns that emerge from specific angular velocity settings:
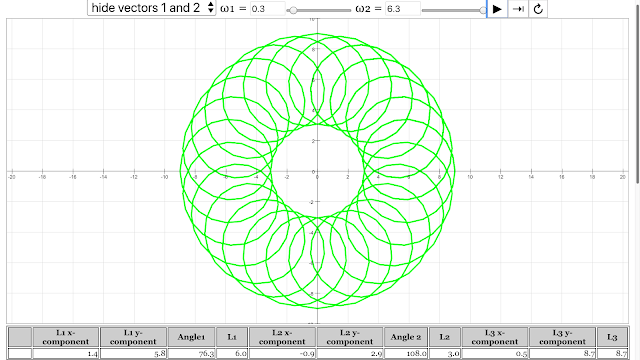
Coil: "angular velocity of vector 1 = 0.3 rad/s, angular velocity of vector 2 = 6.3 rad/s"
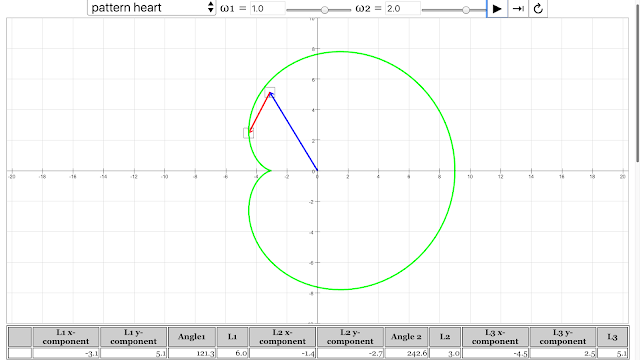
Heart: "angular velocity of vector 1 = 1 rad/s, angular velocity of vector 2 = 2 rad/s"
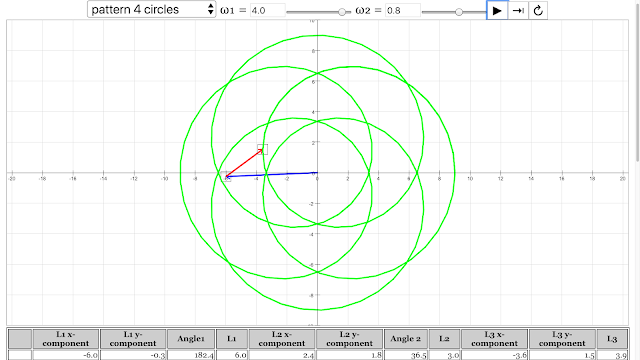
4 circles: "angular velocity of vector 1 = 4 rad/s, angular velocity of vector 2 = 0.8 rad/s"
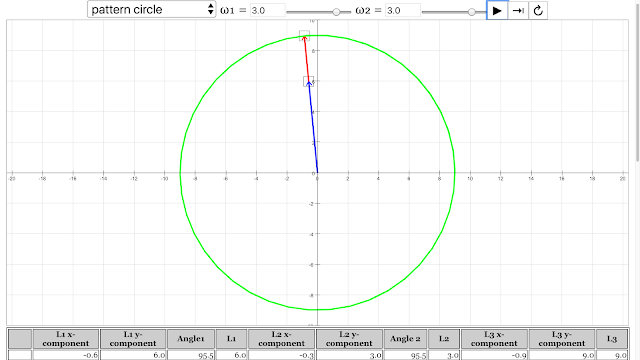
Circle: "angular velocity of vector 1 = 3 rad/s, angular velocity of vector 2 = 3 rad/s"
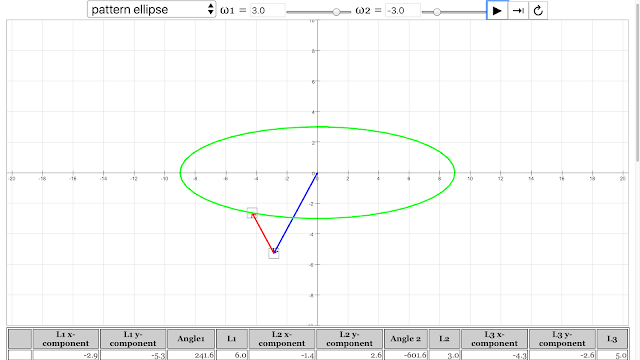
Ellipse: "angular velocity of vector 1 = 3 rad/s, angular velocity of vector 2 = -3 rad/s"
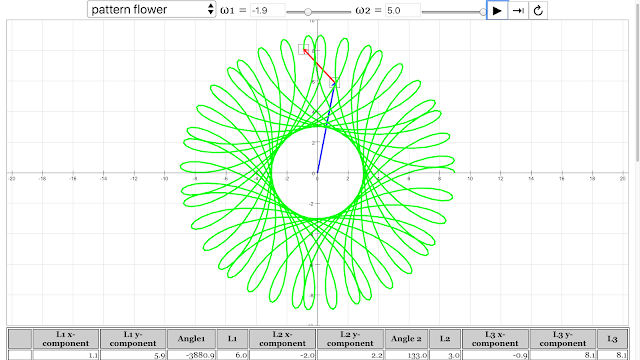
Flower: "angular velocity of vector 1 = -1.9 rad/s, angular velocity of vector 2 = 5 rad/s" These examples demonstrate the potential for complex and aesthetically pleasing shapes to arise from simple vector addition with varying rotational parameters.
Educational Alignment: The simulation aligns with AAAS Benchmarks for Science Literacy, specifically "11B. Models" for grades 9-12. The benchmark emphasizes the power of computers in mathematical modeling, allowing for complex computations and the visualization of their consequences. The description explicitly states: "Computers have greatly improved the power and use of mathematical models by performing computations that are very long, very complicated, or repetitive... The graphic capabilities of computers make them useful... in the simulation of complicated processes." This highlights the pedagogical value of the applet.
Open Educational Resource: The resource is presented as an "Open Educational Resource" (OER) and "Open Source Physics @ Singapore" project. The copyright information in the "Vector Addition Patterns Model" source further reinforces this, stating it is "Released under a license." This implies the resource is freely available for educational use and potentially modification.
Technical Details: The simulation is a "JavaScript HTML5 Applet Simulation Model," indicating its accessibility through web browsers without the need for additional plugins. It was "Compiled with EJS 6.0 (191124)," referring to the Easy JavaScript Simulations authoring tool.
Creators and Affiliation: The simulation was created by Andrew Duffy and Loo Kang Wee, associated with "Open Educational Resources / Open Source Physics @ Singapore."
Availability and Embedding: The resource provides an embed code ("<iframe width="100%" height="100%" src="https://iwant2study.org/lookangejss/01_measurement/ejss_model_vector_addition_sim2_v4/vector_addition_sim2_v4_Simulation.xhtml " frameborder="0">") allowing educators to easily integrate the simulation into their own webpages. Direct links to the model are also provided.
Related Resources and Versions: The sources list various related resources and different versions of the simulation, suggesting an ongoing development and a broader context of learning materials related to vectors and physics.

Quotes from the Original Sources:

"This simulation illustrates the tail-to-tip method of adding vectors." (Vector Addition Pattern Creativity Lesson)
"The table at the bottom shows the components and lengths of the vectors." (Vector Addition Pattern Creativity Lesson)
"You can also rotate the vectors and trace out some interesting patterns." (Vector Addition Pattern Creativity Lesson)
"Adjust the lengths of the two vectors and their rotation rates, and then hit Play. See what kind of interesting patterns you can make, just by adding vectors." (Vector Addition Pattern Creativity Lesson - Activity 4)
"11B. Models 9-12: 11B/H2. Computers have greatly improved the power and use of mathematical models by performing computations that are very long, very complicated, or repetitive. Therefore, computers can reveal the consequences of applying complex rules or of changing the rules. The graphic capabilities of computers make them useful in the design and simulated testing of devices and structures and in the simulation of complicated processes." (Vector Addition Pattern Creativity Lesson - AAAS Benchmark Alignments)
"The pattern of coil emerged from angular velocity of vector 1 = 0.3 rad/s, angular velocity of vector 2 = 6.3 rad/s" (Vector Addition Pattern Creativity Lesson - For Teachers)
"© 2020, Andrew Duffy; Loo Kang Wee. Compiled with EJS 6.0 (191124) Released under a license." (Vector Addition Patterns Model)

Conclusion:

The "Vector Addition Pattern Creativity Lesson JavaScript HTML5 Applet Simulation Model" is a valuable OER tool for teaching vector addition. It combines the fundamental principles of vector mathematics with an engaging and creative exploration of emergent patterns. By allowing users to manipulate vector properties and observe the resulting visual outputs, the simulation fosters a deeper intuitive understanding of vector addition and its applications, aligning with established educational benchmarks for the use of computational models in science education. The provided examples of patterns and the suggested activities offer a structured yet open-ended approach to learning and discovery.

Vector Addition and Pattern Generation Study Guide

Quiz

Explain the tail-to-tip method of vector addition as illustrated by the simulation. How does this method visually represent the resultant vector?
Given two vectors, describe the conditions under which their resultant vector will have its maximum possible magnitude. What will be the direction of this resultant vector relative to the original vectors?
Similarly, explain the conditions required for two vectors to produce a resultant vector with its minimum possible magnitude. What is the relationship between the directions of the original vectors in this case?
How are the x and y components of a vector determined from its magnitude and angle in a two-dimensional plane? Provide the general trigonometric relationships.
According to the "AAAS Benchmark Alignments," how have computers enhanced the use of mathematical models? Give a specific example from the context of the vector addition simulation.
The simulation allows users to adjust the lengths and rotation rates of the vectors. How do these adjustments affect the resultant vector and the patterns traced out?
What role does the angular velocity of each vector play in the generation of the various patterns observed in the simulation (e.g., coil, heart, circles)?
Describe how the simulation can be used as a tool for creative exploration in mathematics and physics, beyond just understanding vector addition.
What are some of the learning goals that students might achieve by interacting with this vector addition pattern simulation? Provide at least two specific examples.
The simulation is built using JavaScript and HTML5. Why are these technologies suitable for creating interactive physics simulations that can be embedded in web pages?

Quiz Answer Key

The tail-to-tip method involves placing the tail (starting point) of the second vector at the tip (ending point) of the first vector. The resultant vector is then drawn from the tail of the first vector to the tip of the second vector, visually representing the sum of the two vectors.
The maximum magnitude of the resultant vector occurs when the two vectors are oriented in the same direction (i.e., the angle between them is 0 degrees). The resultant vector will have a magnitude equal to the sum of the magnitudes of the individual vectors and will point in the same direction.
The minimum magnitude of the resultant vector occurs when the two vectors are oriented in opposite directions (i.e., the angle between them is 180 degrees). The resultant vector will have a magnitude equal to the absolute difference of the magnitudes of the individual vectors and will point in the direction of the vector with the larger magnitude.
For a vector with magnitude r and angle θ with respect to the positive x-axis, the x-component is given by rcos(θ) and the y-component is given by rsin(θ).
Computers have improved the power and use of mathematical models by enabling the performance of very long, complicated, or repetitive computations. In the vector addition simulation, computers allow for the continuous calculation and display of the resultant vector as the individual vectors rotate, revealing complex patterns that would be difficult to predict or visualize manually.
Adjusting the lengths of the vectors changes their magnitudes, directly affecting the magnitude and scale of the resultant vector and the traced patterns. Changing the rotation rates (angular velocities) alters how quickly the vectors change orientation, leading to different frequencies and shapes in the generated patterns.
The angular velocity of each vector determines how quickly it rotates. The interplay between the different angular velocities of the two vectors leads to the complex and varied patterns observed. For example, specific ratios and values of angular velocities result in distinct shapes like the heart or the four circles.
Beyond understanding vector addition, the simulation allows for creative exploration by enabling users to experiment with different vector properties and observe the resulting visual patterns. This can foster intuitive understanding of how vector combinations lead to emergent behaviors and artistic designs, connecting mathematical concepts to visual outcomes.
Possible learning goals include: understanding the graphical representation of vector addition using the tail-to-tip method, exploring how the magnitude and direction of a resultant vector depend on the magnitudes and directions of its component vectors, investigating the concept of vector components, and recognizing the relationship between angular velocity and the patterns generated by the sum of rotating vectors.
JavaScript is a versatile scripting language that can create dynamic and interactive web content, while HTML5 provides the structure and elements for web pages, including canvas elements for graphics rendering. This combination allows for the creation of platform-independent simulations that can run directly in web browsers without the need for additional plugins.

Essay Format Questions

Discuss the pedagogical benefits of using interactive simulations like the Vector Addition Pattern Creativity Lesson in teaching vector addition. How does this approach compare to traditional methods, and what are its advantages in promoting student understanding and engagement?
Explore the relationship between the mathematical concept of vector addition and the artistic patterns that can be generated through this simulation. How can manipulating vector properties (magnitude, angle, angular velocity) lead to the creation of diverse and complex visual designs?
Analyze how the Vector Addition Pattern Creativity Lesson aligns with the "AAAS Benchmark Alignments" regarding the use of computers in mathematical modeling. Provide specific examples from the simulation to illustrate how it demonstrates the power of computation in revealing the consequences of applying rules and visualizing complex processes.
Consider the role of open educational resources like this simulation in democratizing access to physics education. What are the potential impacts of freely available interactive tools on student learning and the broader educational landscape?
Imagine you are a teacher using this simulation in your classroom. Describe a specific activity or lesson plan you would implement, outlining the learning objectives, the steps students would take while interacting with the simulation, and how you would assess their understanding of the concepts.

Glossary of Key Terms

Vector: A quantity that has both magnitude (size) and direction. It is often represented graphically as an arrow.
Magnitude: The length or size of a vector, representing the amount of the quantity it describes.
Direction: The orientation of a vector in space, often specified by an angle relative to a reference axis.
Resultant Vector: The single vector that is the sum of two or more vectors. It represents the net effect of the individual vectors acting together.
Tail-to-Tip Method: A graphical method of adding vectors where the tail of the second vector is placed at the tip of the first vector. The resultant vector is drawn from the tail of the first to the tip of the second.
Vector Components: The projections of a vector onto coordinate axes (typically x and y in two dimensions). They represent the parts of the vector that act along each axis.
Angular Velocity: The rate at which an object rotates or revolves relative to a center point, usually measured in radians per second (rad/s). In this simulation, it refers to the rate of change of the angle of each vector.
Simulation: A computer program that models a real-world system or process, allowing users to interact with and observe its behavior.
JavaScript: A high-level, often just-in-time compiled programming language that conforms to the ECMAScript specification. It is commonly used to make web pages interactive.
HTML5: The latest evolution of the standard that defines HTML. It is used for structuring and presenting content on the World Wide Web and includes features for multimedia and interactive elements.
Open Educational Resources (OER): Teaching, learning, and research materials that are in the public domain or released with an open license that permits their free use and re-purposing by others.

Sample Learning Goals

AAAS Benchmark Alignments (2008 Version)

11. Common Themes

11B. Models

9-12: 11B/H2. Computers have greatly improved the power and use of mathematical models by performing computations that are very long, very complicated, or repetitive. Therefore, computers can reveal the consequences of applying complex rules or of changing the rules. The graphic capabilities of computers make them useful in the design and simulated testing of devices and structures and in the simulation of complicated processes.

For Teachers

The pattern of coil emerged from angular velocity of vector 1 = 0.3 rad/s, angular velocity of vector 2 = 6.3 rad/s

Vector Addition Pattern Creativity Lesson JavaScript HTML5 Applet Simulation Model