About

Symmetry operations

Rotation, mirroring and inversion are noncommutative and hence non Abelian transformation operations in set theory. The result depends on the sequence of operations.

The simulation demonstrates this for the operations of rotation and mirroring, applied to a triangle.

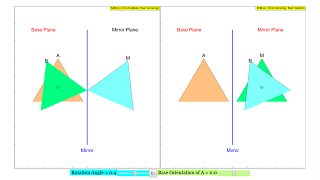
When the simulation is started, one sees two identical coordinate systems, with a mirror located at the center x = 0 of each. At its left side there is a triangle with its base initially parallel to the x axis. Its upper edge is marked by the letter A. The triangle is pink in color. At the right side of the mirror one sees the mirror image of the triangle, marked by a letter M, and colored in blue

The slider Base Orientation defines the orientation of the original triangle. One observes the counterclockwise rotation of the mirror image, which is the same in both charts.

The slider Rotation Angle creates a rotation operation on the object in its base orientation.

In the left chart the rotation is operated on the object A, and the mirror image M of the rotated object R is displayed. In the right chart the rotation is operated on the mirrored object M and results in a different R. The sequence of operations is discernable by the coloring of the triangles: green is first, blue is second.

The left chart displays the mirrored-rotated object, the right one the rotated-mirrored object. In general both are different in orientation. The transformation operations are noncommutative.

Reset restores the initial orientation.

This file was created by Dieter Roess in November 2009

This simulation is part of

“Learning and Teaching Mathematics using Simulations

– Plus 2000 Examples from Physics”

ISBN 978-3-11-025005-3, Walter de Gruyter GmbH & Co. KG

 

Translations

Code	Language		Translator	Run

Credits

Dieter Roess - WEH- Foundation; Tan Wei Chiong; Loo Kang Wee

1. Introduction:

This briefing document reviews the key themes, concepts, and functionalities presented in the description of the "Symmetry Operations JavaScript Simulation Applet HTML5" available on the Open Educational Resources / Open Source Physics @ Singapore website. The simulation focuses on illustrating the noncommutative nature of symmetry operations, specifically rotation and mirroring.

2. Main Themes and Important Ideas:

• Noncommutative Nature of Symmetry Operations: The central theme of the simulation is to demonstrate that the order in which symmetry operations are applied affects the final result. The description explicitly states, "Rotation, mirroring and inversion are noncommutativ e and hence non Abelian transformation operations in set theory. The result depends on the sequence of operations." This concept is fundamental in areas of mathematics and physics dealing with symmetry, such as group theory, crystallography, and quantum mechanics.
• Visualization of Rotation and Mirroring: The simulation provides a visual and interactive way to understand how rotation and mirroring transform an object (a triangle in this case). It presents two parallel coordinate systems, each with a mirror, allowing for a direct comparison of the outcomes when the order of rotation and mirroring is reversed.
• Interactive Learning Tool: The applet is designed as an educational resource, allowing users to manipulate parameters like "Base Orientation" and "Rotation Angle" using sliders. This interactivity enables learners to actively explore the effects of different symmetry operations and the impact of their sequence. The "Reset" button allows users to easily return to the initial state for further experimentation.
• Distinction Between Mirrored-Rotated and Rotated-Mirrored Objects: The simulation clearly distinguishes between applying mirroring first and then rotation, versus applying rotation first and then mirroring. The left chart shows the "mirrored-rotated object," while the right chart displays the "rotated-mirrored object." The description highlights that "[i]n general both are different in orientation," directly illustrating the noncommutativity.
• Color-Coding for Operation Sequence: To further clarify the order of operations, the simulation uses color-coding of the triangles: "green is first, blue is second." This visual cue helps users track which operation was applied at each step in both the left and right charts.
• Target Audience: Learning and Teaching Mathematics and Physics: The simulation is explicitly mentioned as part of a larger resource titled "Learning and Teaching Mathematics using Simulations – Plus 2000 Examples from Physics." This indicates its intended use in educational settings for both students and teachers. The "For Teachers" section reinforces this by providing a concise explanation of the simulation's purpose and how it can be used to teach the concept of noncommutative symmetry operations.

3. Key Functionalities and Visual Elements:

• Two Identical Coordinate Systems: These provide a side-by-side comparison of the two different sequences of operations.
• Central Mirror (x = 0): Located in each coordinate system, the mirror performs the mirroring operation.
• Pink Original Triangle (A): Located on the left side of the left coordinate system, with its base initially parallel to the x-axis.
• Blue Mirror Image Triangle (M): Located on the right side of each mirror, representing the mirrored version of the triangle.
• Sliders for "Base Orientation" and "Rotation Angle": These interactive elements allow users to control the initial orientation of the triangle and the degree of rotation applied.
• Rotated Object (R): Displayed in both charts after the rotation operation, the color of this triangle indicates whether it was rotated first (green) or second (blue).
• "Reset" Button: Restores the simulation to its initial configuration.
• Embed Option: Provides an iframe code snippet, allowing educators to easily integrate the simulation into their own web pages.

4. Target Learning Outcomes (Implied):

Based on the description and the "For Teachers" section, the simulation aims to help learners understand:

• The concept of symmetry operations (rotation and mirroring).
• That the order of applying these operations matters.
• The mathematical property of noncommutativity through a visual and interactive example.

5. Supporting Information:

• Authorship and Credits: The simulation was created by Dieter Roess in November 2009, with contributions from Tan Wei Chiong and Loo Kang Wee. The development was supported by the WEH- Foundation.
• Context: The simulation is part of a larger educational resource, "Learning and Teaching Mathematics using Simulations – Plus 2000 Examples from Physics," suggesting a broader pedagogical framework.
• Licensing: The content is licensed under the Creative Commons Attribution-Share Alike 4.0 Singapore License, promoting open access and sharing for educational purposes. The EasyJavaScriptSimulations Library used for development has a separate commercial use license.
• Related Resources: The page includes links to other simulations and educational tools available on the platform, showcasing the breadth of resources offered by Open Educational Resources / Open Source Physics @ Singapore.

6. Conclusion:

The "Symmetry Operations JavaScript Simulation Applet HTML5" is a valuable open educational resource for teaching and learning about the noncommutative nature of symmetry operations. Its interactive and visual approach, coupled with clear explanations and user-friendly controls, makes it an effective tool for illustrating abstract mathematical and physical concepts. The ability to embed the simulation further enhances its utility for educators seeking to integrate interactive learning experiences into their teaching materials.

 

Symmetry Operations Study Guide

Key Concepts

• Symmetry Operations: Transformations that leave an object looking the same after the operation is performed. The text specifically discusses rotation and mirroring.
• Noncommutative Operations: Operations where the order in which they are performed affects the final result. In mathematical notation, for two operations A and B, A followed by B is not the same as B followed by A (A * B ≠ B * A).
• Non-Abelian Transformations: Another term for noncommutative transformations in the context of set theory and abstract algebra.
• Rotation: A transformation that turns an object around a fixed point (the center of rotation) by a certain angle.
• Mirroring: A transformation that creates a reflection of an object across a plane (the mirror). In this simulation, the mirror is located at x = 0.
• Coordinate System: A framework used to define the position of points in space. The simulation uses two identical coordinate systems.
• Mirror Image: The reflection of an object across a mirror plane.

Quiz

1. What two symmetry operations are specifically demonstrated in the JavaScript simulation?
2. Explain in your own words what it means for two operations to be noncommutative.
3. According to the text, what is the consequence of rotation and mirroring being noncommutative operations?
4. In the simulation, where is the mirror located in each of the two coordinate systems?
5. Describe the initial setup of the triangle on the left side of the simulation when it starts.
6. What does the "Base Orientation" slider control in the simulation?
7. What is the difference in how the rotation operation is applied in the left and right charts of the simulation?
8. How does the simulation visually indicate the sequence in which the rotation and mirroring operations are performed?
9. What general conclusion can be drawn by observing the final orientation of the triangles in the left and right charts after applying rotation and mirroring?
10. What action does the "Reset" button perform in the simulation?

Quiz Answer Key

1. The two symmetry operations demonstrated in the JavaScript simulation are rotation and mirroring.
2. For two noncommutative operations, the order in which you perform them matters; applying operation A then operation B will yield a different result than applying operation B then operation A.
3. Because rotation and mirroring are noncommutative, the final result of applying both operations to an object depends on which operation is performed first.
4. In the simulation, the mirror is located at the center x = 0 of each of the two identical coordinate systems.
5. When the simulation starts, on the left side there is a pink triangle with its base initially parallel to the x-axis and its upper edge marked with the letter A.
6. The "Base Orientation" slider defines the initial rotational orientation of the original triangle in both charts.
7. In the left chart, the rotation is applied to the original triangle (A) first, and then the rotated object is mirrored (resulting in M of the rotated object R). In the right chart, the original triangle is mirrored (M) first, and then the mirror image is rotated (resulting in a different R).
8. The sequence of operations is shown by the coloring of the triangles: the triangle resulting from the first operation is green, and the triangle resulting from the second operation is blue.
9. The general conclusion is that the mirrored-rotated object (left chart) and the rotated-mirrored object (right chart) have different final orientations, illustrating the noncommutative nature of the operations.
10. The "Reset" button restores the triangles and mirrors to their initial orientation as seen when the simulation is first started.

Essay Format Questions

1. Discuss the significance of the simulation demonstrating noncommutative symmetry operations using rotation and mirroring. Why is the order of operations important in various scientific and mathematical contexts?
2. Explain how the JavaScript simulation visually represents the concept of noncommutativity. Analyze the role of the two panels and the coloring of the triangles in conveying this idea.
3. Beyond rotation and mirroring, what are some other examples of transformations that might be noncommutative? Briefly describe a scenario where the order of these transformations would lead to different outcomes.
4. How could this JavaScript simulation be used as a teaching tool to help students understand abstract mathematical concepts like noncommutative operations? Discuss its strengths and potential limitations in an educational setting.
5. The simulation focuses on a simple geometric shape (a triangle). How might the demonstration of noncommutative symmetry operations differ if applied to more complex objects or in higher dimensions?

Glossary of Key Terms

• Symmetry Operation: An action performed on an object that results in the object appearing identical to its original state after the operation.
• Rotation: Turning an object around a fixed point or axis. The amount of rotation is typically specified by an angle.
• Mirroring (Reflection): Creating a mirror image of an object across a plane of symmetry. Every point in the original object has a corresponding point in the reflected object equidistant from the mirror plane.
• Inversion: A symmetry operation where every point of an object is transformed through a central point (the inversion center) to a point located at an equal distance on the opposite side. While mentioned in the text as noncommmutative, it is not explicitly demonstrated in the simulation.
• Noncommutative: A property of operations where the result depends on the order in which the operations are performed. If operation A followed by operation B is different from operation B followed by operation A, then A and B are noncommutative.
• Non-Abelian: A mathematical term, particularly in group theory, referring to a group where the group operation is not commutative. The text uses this term synonymously with noncommutative in the context of transformation operations in set theory.
• Transformation: An operation that changes the position, size, shape, or orientation of an object. Rotation and mirroring are types of transformations.
• Simulation: A computer-based model that imitates a real-world process or system, allowing users to interact with it and observe the outcomes of different actions or parameters.
• Coordinate System: A system that uses one or more numbers (coordinates) to uniquely determine the position of a point or other geometric element. The Cartesian coordinate system (with x and y axes) is implied in the simulation's description.
• Applet: A small application, often written in Java or JavaScript, that runs within another application, typically a web browser. The simulation described is a JavaScript applet.

Sample Learning Goals

[text]

For Teachers

If you first apply a rotation to a object, then mirror that rotated object, you'll find that what you get is different than if you first applied the mirroring, then the rotation.

There are two panels in this simulation: the left panel shows what happens when you first apply rotation, then the mirroring. the right panel shows what happens when the mirroring is first applied, then the rotation.

The rotation and base orientation of the triangle A can be adjusted using the sliders provided.

Research

[text]

Video

[text]

 Version:

1. http://weelookang.blogspot.sg/2016/02/vector-addition-b-c-model-with.html improved version with joseph chua's inputs
2. http://weelookang.blogspot.sg/2014/10/vector-addition-model.html original simulation by lookang

Other Resources

[text]

Frequently Asked Questions: Symmetry Operations Simulation

1. What does this simulation demonstrate?

This simulation demonstrates the concept of symmetry operations, specifically rotation and mirroring, and highlights that these operations are generally noncommutative. This means that the order in which these operations are applied to an object affects the final result.

2. How does the simulation illustrate noncommutativity?

The simulation uses a triangle and applies rotation and mirroring operations in two different sequences. In the left panel, a rotation is applied first, and then the result is mirrored. In the right panel, mirroring is applied first, and then the result is rotated. By observing the final orientation and color of the triangles in both panels, users can see that the outcomes are different, thus demonstrating that the order of operations matters.

3. What are the controls available in the simulation?

The simulation provides sliders to adjust the "Base Orientation" of the initial triangle and the "Rotation Angle" for the rotation operation. The "Base Orientation" slider rotates both the original triangle and its initial mirror image. The "Rotation Angle" slider applies a counterclockwise rotation to the object in its current orientation in each panel. A "Reset" button is also available to restore the initial setup.

4. What do the colors of the triangles signify?

The colors of the triangles indicate the sequence of operations performed. A green triangle represents the state after the first operation, and a blue triangle represents the state after the second operation. This visual cue helps users track the order of transformations in each panel.

5. Where is the mirror located in the simulation?

In both coordinate systems displayed in the simulation, a mirror is located at the center, specifically at the vertical line x = 0.

6. What is the purpose of having two identical coordinate systems in the simulation?

The two identical coordinate systems serve to illustrate the effect of applying the rotation and mirroring operations in different orders simultaneously. The left panel shows the result of rotation followed by mirroring, while the right panel shows the result of mirroring followed by rotation, allowing for a direct visual comparison of the noncommutative nature of these operations.

7. Who created this simulation and for what purpose?

This simulation was created by Dieter Roess in November 2009. It is part of the "Learning and Teaching Mathematics using Simulations – Plus 2000 Examples from Physics" project, which aims to use interactive simulations to enhance the understanding of mathematical and physical concepts.

8. For whom is this simulation intended?

This simulation is intended for learners and teachers of mathematics and physics. It provides a visual and interactive way to understand the abstract concept of noncommutative operations in set theory and their application in geometric transformations like rotation and mirroring.