About

Spontaneous perception of cardinal numbers

(Members in a set )

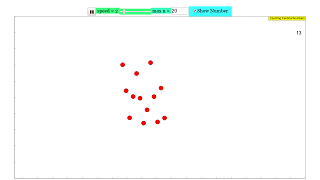
When the simulation is opened a field is shown with some red dots in random distribution. They are sufficiently close to perceive their number at a glance.

The number of points displayed is changed periodically at random between 1 and a maximum number that can be edited in the number field. Default value is a maximum of 5 dots.

A slider defines the changes per second between 1 and 10.

A narrow second window shows how many points are displayed at any moment. This window can be concealed by a check box. It can also be drawn out of the field of view of the experimenting person to allow control by a second person.

Try to perceive with certainty the number of points without counting (scanning).

Up to 5 points this should be no problem. Beyond 7 it will be barely possible. This finding does not vary substantially with moderate changes in the speed of presentation.

Spontaneus perception and skill of calculation

Cardinal numbers indicate the number of elements in a set, i.e. the number of elements in a group with some common identifiable quality (not necessarily identity!) Even very young children will identify 2 apples, which of course are not identical in their appearance in a mathematical sense, as 2 apples.

Ordinal numbers characterize the consecution of elements in a set. Young children will count a number of apples in a row as 1, 2, 3 and identify a certain element as 3, meaning it is the third one.

To the skilled adult this differentiation blurs when calculating. When asked 3 + 5 he will immediately answer 8, as if having added the cardinal numbers 3 and 5.

A young child solves the same problem openly using ordinal numbers, starting with counting the first row 1st, 2nd, 3rd, and continuing in the second row 4th, 5th, 6th, 7th, 8th. Alas! The result is 8.

For children of about 3 years it is a difficult task to calculate with ordinal numbers even for very small numbers. Yet they love to do it as a game. It takes a lot of repetition and exercise to climb from 1 + 1 (which is grasped very quickly) to 4 + 1 , and it is very charming how they use their fingers, open or concealed, to "cheat" by counting.

Quite surprisingly one never gets much beyond 5 in the spontaneous perception of cardinal numbers. Any skill to do fast addition beyond that small number range is the result of memorizing the outcome of numerous combinations and of rules, and hence of hard work. Insofar persistent exercise in basic calculation and the learning of multiplication tables is no boring ill treatment of kids, but the basis of an indispensible cultural skill.

Most adults do not realize that their skill in the perception of cardinal numbers does not go beyond that of young children (and that of well trainable animals, by the way), and that it cannot really be trained. Their skill (if they have it!) is based on a history of memorization of results and rules.

E1: Conceal the number window and let the animation run at 1 step per second, and for a maximum of 5 points.

Do you always recognize the number of points without counting or scanning?

E2: Increase the speed − which makes counting more difficult. Do you experience a great difference?

E3: Increase the maximum number and test where your limit of secure perception is at different speeds.

E4: Test if you perceive this limit consistently or just when the points form a regular pattern.

E5: Let another person control you.

E6: Draw a diagram of the number of true hits as a function of the maximum number of points, and another one of the dependence on speed.

E7: Let your friends bet on their maximum, and show them their limit.

E8: Try to draw conclusions on what your findings mean when applied to the teaching of young children.

This file was created by Dieter Roess in December 2009

This simulation is part of

“Learning and Teaching Mathematics using Simulations

– Plus 2000 Examples from Physics”

ISBN 978-3-11-025005-3, Walter de Gruyter GmbH & Co. KG

 

Translations

Code	Language		Translator	Run

Credits

Dieter Roess - WEH- Foundation; Tan Wei Chiong; Loo Kang Wee

• Overview:

  This document provides a briefing on the main themes and important ideas presented in the "Spontaneous Perception of Cardinal Numbers JavaScript Simulation Applet HTML5" resource from Open Educational Resources / Open Source Physics @ Singapore. The resource describes a JavaScript simulation designed to explore the human ability to instantly perceive the number of items in a set without counting, focusing on the distinction between cardinal and ordinal numbers and the implications for early mathematics education.

  Main Themes and Important Ideas:

  1. Spontaneous Perception of Cardinal Numbers (Subitizing):
  • The core concept explored is the "spontaneous perception of cardinal numbers," also known as subitizing, which refers to the ability to instantly recognize the number of elements in a small set without needing to count them individually.
  • The simulation displays a field of randomly distributed red dots, changing the number periodically between 1 and a user-defined maximum (default 5). The goal is to perceive the number of dots at a glance without counting.
  • The resource highlights the limited capacity of this ability: "Up to 5 points this should be no problem. Beyond 7 it will be barely possible." This limitation is presented as relatively consistent regardless of the speed of presentation.
  1. Cardinal vs. Ordinal Numbers:
  • The resource clearly distinguishes between cardinal and ordinal numbers, explaining their fundamental differences and how children initially understand them.
  • Cardinal numbers are defined as indicating "the number of elements in a set." The example provided is: "Even very young children will identify 2 apples, which of course are not identical in their appearance in a mathematical sense, as 2 apples."
  • Ordinal numbers are defined as characterizing "the consecution of elements in a set," referring to the position of an item in a sequence. An example is counting apples in a row as "1st, 2nd, 3rd," where "3rd" identifies a specific element's position.
  • The text notes that while adults often blur this distinction in calculation, young children initially rely on ordinal counting to solve addition problems.
  1. The Development of Calculation Skills:
  • The resource contrasts the innate ability of spontaneous perception with the learned skill of calculation.
  • It observes that young children initially struggle with calculating even small numbers using ordinal counting but find it engaging as a game.
  • The development of calculation beyond small numbers (around 5) is attributed to "memorizing the outcome of numerous combinations and of rules, and hence of hard work."
  • The resource argues that "persistent exercise in basic calculation and the learning of multiplication tables is no boring ill treatment of kids, but the basis of an indispensible cultural skill."
  1. Limitations of Adult Cardinal Number Perception:
  • A key point is that "Most adults do not realize that their skill in the perception of cardinal numbers does not go beyond that of young children... and that it cannot really be trained."
  • Adults' proficiency in quick arithmetic is attributed to "a history of memorization of results and rules," rather than an enhanced ability to spontaneously perceive larger cardinal numbers.
  1. The JavaScript Simulation as a Learning Tool:
  • The resource introduces a JavaScript simulation applet (embed code provided) as a tool to explore these concepts.
  • The simulation allows users to manipulate the number of dots displayed, the speed of change, and the visibility of the actual number.
  • It suggests several experiments (E1-E7) that users can conduct to test their own limits of spontaneous perception under different conditions.
  • Experiment E8 specifically encourages users to "Try to draw conclusions on what your findings mean when applied to the teaching of young children."
  1. Implications for Teaching Young Children:
  • The findings from exploring spontaneous perception have direct implications for early mathematics education.
  • The resource implicitly suggests that teaching methods should acknowledge the natural limitations of subitizing and the initial reliance of children on ordinal counting.
  • It emphasizes the importance of building a strong foundation through practice and memorization for developing more advanced calculation skills, refuting the idea that such exercises are merely tedious.

  Key Quotes:

  • "When the simulation is opened a field is shown with some red dots in random distribution. They are sufficiently close to perceive their number at a glance." (Description of the simulation)
  • "Up to 5 points this should be no problem. Beyond 7 it will be barely possible." (On the limit of spontaneous perception)
  • "Cardinal numbers indicate the number of elements in a set..."
  • "Ordinal numbers characterize the consecution of elements in a set..."
  • "Quite surprisingly one never gets much beyond 5 in the spontaneous perception of cardinal numbers. Any skill to do fast addition beyond that small number range is the result of memorizing the outcome of numerous combinations and of rules, and hence of hard work."
  • "Most adults do not realize that their skill in the perception of cardinal numbers does not go beyond that of young children... and that it cannot really be trained. Their skill (if they have it!) is based on a history of memorization of results and rules."
  • "persistent exercise in basic calculation and the learning of multiplication tables is no boring ill treatment of kids, but the basis of an indispensible cultural skill." (On the importance of practice)

  Conclusion:

  The "Spontaneous Perception of Cardinal Numbers JavaScript Simulation Applet HTML5" resource provides a valuable and interactive way to understand the cognitive processes involved in number recognition and early mathematical development. It highlights the distinction between innate subitizing abilities and learned calculation skills, emphasizing the limitations of the former and the importance of practice and memorization for the latter. The resource encourages educators and learners to explore these concepts through the provided simulation and consider the implications for teaching and learning mathematics, particularly in early childhood.

1. Study Guide: Spontaneous Perception of Cardinal Numbers

   Key Concepts:

   • Cardinal Numbers: Numbers indicating the quantity of elements in a set.
   • Ordinal Numbers: Numbers indicating the position of elements in a sequence.
   • Spontaneous Perception: The ability to instantly recognize the number of items without counting.
   • Subitizing: The perceptual process by which we can instantly recognize the quantity of a small number of objects (typically up to 3-5).
   • Cognitive Load: The mental effort required to perform a task. Counting larger numbers of items increases cognitive load.
   • Memorization in Calculation: The process by which adults perform quick arithmetic through recalling learned facts and rules, rather than relying on counting.

   Quiz:

   1. What is the primary difference between cardinal and ordinal numbers, according to the text? Provide an example of each.
   2. Describe the JavaScript simulation applet. What is the main purpose of the red dots displayed?
   3. What is the typical limit for spontaneous perception of cardinal numbers in most individuals, as suggested by the text and the simulation's design?
   4. Explain why young children often use ordinal numbers when first learning to add, even for simple calculations.
   5. How does the text suggest that adults are able to perform arithmetic quickly, even though their spontaneous perception of quantity is limited?
   6. Describe Experiment E1 from the text. What is the main question it aims to explore?
   7. According to the text, does increasing the speed of presentation significantly alter the limit of spontaneous perception of cardinal numbers?
   8. What does the text imply about the trainability of spontaneous cardinal number perception beyond the typical limit?
   9. Why does the author argue that persistent exercise in basic calculation and learning multiplication tables is important for children?
   10. What is one practical implication for teaching young children that can be drawn from the findings about spontaneous perception of cardinal numbers?

   Answer Key:

   1. Cardinal numbers indicate the number of elements in a set (e.g., "There are five apples"). Ordinal numbers indicate the position of an element in a sequence (e.g., "This is the third apple in the row").
   2. The applet displays a field with a random distribution of red dots, the number of which changes periodically. The main purpose of these dots is to allow users to test their ability to spontaneously perceive the quantity without counting.
   3. The typical limit for spontaneous perception of cardinal numbers is around 5 to 7 items. Beyond this number, accurate recognition usually requires counting or scanning.
   4. Young children often use ordinal numbers for addition by sequentially counting through the elements of each set. For example, for 3 + 5, they might count "1st, 2nd, 3rd" and then continue "4th, 5th, 6th, 7th, 8th."
   5. Adults perform arithmetic quickly primarily through memorization of number combinations and arithmetic rules learned over time, rather than through the direct spontaneous perception of quantities.
   6. Experiment E1 involves concealing the number window of the simulation and setting the animation to run at 1 step per second with a maximum of 5 points. It aims to determine if the user can always recognize the number of points without counting or scanning within this limited range.
   7. The text suggests that moderate changes in the speed of presentation do not substantially vary an individual's limit for the spontaneous perception of cardinal numbers.
   8. The text implies that the ability for spontaneous cardinal number perception beyond the 5-7 range is not significantly trainable. Skill in dealing with larger numbers relies on memorization and learned strategies.
   9. The author argues that persistent exercise in basic calculation and learning multiplication tables is not a negative experience but rather the foundation of an essential cultural skill, as it allows individuals to perform arithmetic beyond the limits of spontaneous perception.
   10. One practical implication for teaching young children is to recognize the natural limitations of their spontaneous number perception and to understand that developing calculation skills requires explicit instruction, repetition, and the gradual memorization of number facts.

   Essay Format Questions:

   1. Discuss the distinction between cardinal and ordinal numbers and analyze the role each plays in the early development of mathematical understanding in children, drawing upon the concepts presented in the text.
   2. Analyze the findings of the spontaneous perception simulation and experiments described in the text. How do these findings challenge or support common assumptions about adult numerical abilities and how we perform calculations?
   3. Evaluate the author's argument that the persistent practice of basic calculation and multiplication tables is a crucial "cultural skill" rather than "boring ill treatment." Use evidence from the text about the limitations of spontaneous perception to support your reasoning.
   4. Based on the information provided in the text, design a short activity or teaching strategy that effectively incorporates the principles of spontaneous perception to introduce the concept of cardinal numbers to young children. Explain your rationale.
   5. Explore the implications of the limited capacity for spontaneous perception of cardinal numbers (around 5-7) on more advanced mathematical learning. How might this foundational limitation influence the development of skills in areas such as algebra or more complex arithmetic?

   Glossary of Key Terms:

   • Cardinal Number: A number that denotes a quantity, such as one, two, three. It answers the question "How many?".
   • Ordinal Number: A number that denotes the position of an element in a sequence, such as first, second, third. It indicates order.
   • Spontaneous Perception: The immediate and effortless recognition of a quantity without conscious counting or scanning.
   • Subitizing: The rapid, accurate, and confident judgment of the number of items in a small set (typically 1 to 4 or 5) without counting. It is a form of spontaneous perception for very small numbers.
   • Cognitive Load: The total amount of mental effort being used in the working memory. Tasks requiring counting larger sets increase cognitive load compared to tasks relying on spontaneous perception.
   • Set (in mathematics): A well-defined collection of distinct objects, considered as an object in its own right. Cardinal numbers refer to the number of elements within a set.
   • Consecution: The action of following in order; sequence. Ordinal numbers describe the consecution of elements.

Sample Learning Goals

[text]

For Teachers

Research

[text]

Video

[text]

 Version:

1. http://weelookang.blogspot.sg/2016/02/vector-addition-b-c-model-with.html improved version with joseph chua's inputs
2. http://weelookang.blogspot.sg/2014/10/vector-addition-model.html original simulation by lookang

Other Resources

[text]

What is "spontaneous perception of cardinal numbers" as described in the simulation?

Spontaneous perception of cardinal numbers refers to the ability to instantly recognize the quantity of items in a small set without needing to count them individually. The simulation demonstrates this using red dots that appear briefly, challenging users to identify the number of dots at a glance.

What is the typical limit for spontaneous perception of cardinal numbers in adults and children?

The simulation suggests that for most people, including adults and children, the limit for accurate spontaneous perception of cardinal numbers is around 5 to 7 items. Beyond this number, it becomes very difficult to determine the quantity without counting or scanning.

How does the simulation allow users to explore spontaneous perception of cardinal numbers?

The JavaScript simulation displays a field of red dots, the number of which changes randomly between 1 and a user-defined maximum (default is 5). Users can adjust the speed at which the number of dots changes and can also conceal a window that explicitly shows the number of dots. This setup allows them to test their ability to perceive the quantity without counting under varying conditions of speed and maximum number of items.

What is the difference between cardinal and ordinal numbers, and how do children learn to use them in calculation?

Cardinal numbers indicate the quantity of elements in a set (e.g., three apples), while ordinal numbers indicate the position of elements in a sequence (e.g., the third apple). Young children often initially approach addition problems using ordinal numbers by counting through the sequence (e.g., 1st, 2nd, 3rd, 4th, 5th for 3 + 2), whereas skilled adults directly add the cardinal values.

How does the development of calculation skills relate to the spontaneous perception of cardinal numbers?

The text explains that while spontaneous perception is limited to small numbers (around 5-7), the ability to perform calculations with larger numbers is not based on extending this perceptual skill. Instead, it relies on memorization of number combinations, rules, and consistent practice. Therefore, proficiency in calculation is a learned skill rather than an enhanced ability to spontaneously perceive larger quantities.

What do the experiments suggested in the text aim to demonstrate about number perception?

The suggested experiments (E1-E7) aim to help users discover their personal limits of spontaneous cardinal number perception under different conditions. These include varying the speed of presentation, the maximum number of items, and the consistency of perception with or without regular patterns. The experiments also encourage users to compare their abilities with others.

What implications does the limited spontaneous perception of cardinal numbers have for teaching young children mathematics?

The text suggests that understanding the natural limitations of spontaneous number perception is important for teaching. It highlights that mastering basic calculations requires practice and memorization, and this effort is fundamental to developing mathematical skills. Educators should recognize that children initially use ordinal counting for calculation and need time and repetition to grasp cardinal number operations.

Besides this specific simulation, what other types of interactive learning tools and simulations are offered by Open Educational Resources / Open Source Physics @ Singapore?

The website hosts a wide variety of JavaScript simulations and interactive applets spanning various topics in mathematics and physics. Examples listed include simulations for vector addition, Mandelbrot sets, logistic maps, wave phenomena, electromagnetism, mechanics, optics, and even games for learning mathematical concepts. These resources are designed to enhance learning through interactive exploration.