Credits

['Kang Rui']

Exploring Math Isometric Grid Simulation: A Best Practices Guide for WebEJS

Introduction

link

 

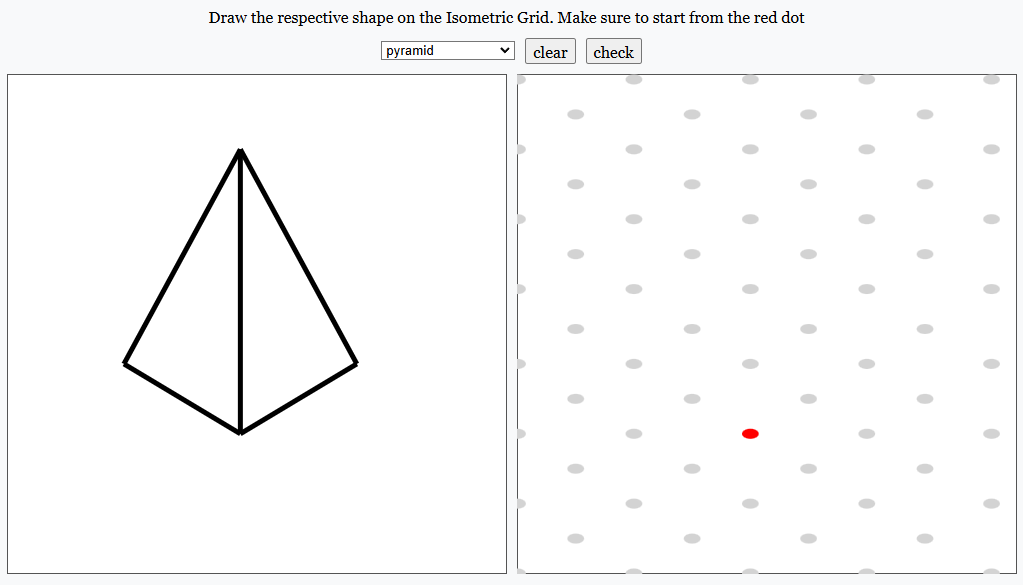
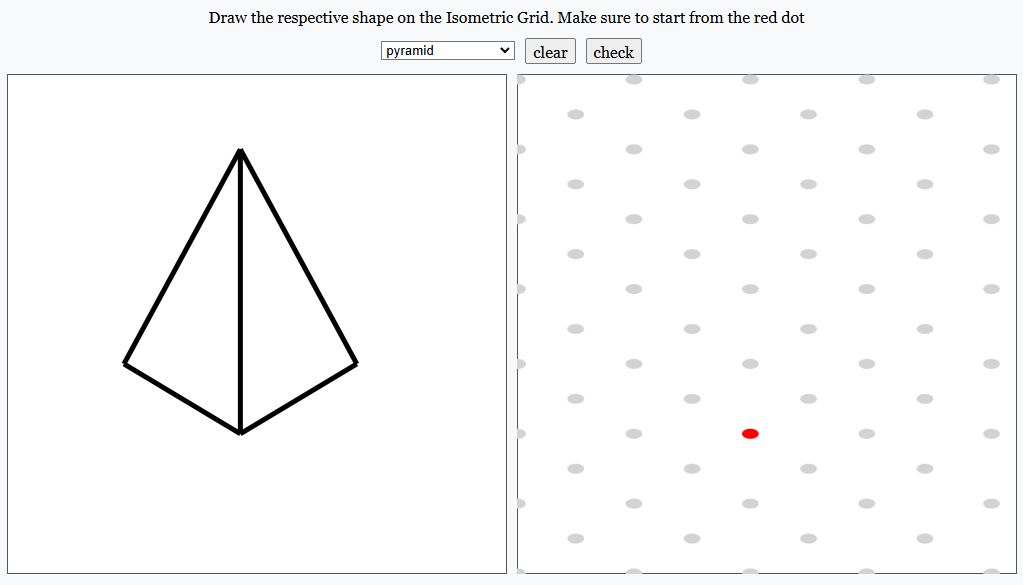
The Math Isometric Grid Simulation (webejs_model_Math_Isometric_Grid_v1) is a versatile educational tool designed to enhance visualization in mathematics education. With features to model geometric shapes like pyramids and cubes on isometric grids, it offers an intuitive way for students to grasp spatial geometry concepts.

Developed with WebEJS, this simulation exemplifies how interactive content can simplify complex concepts, empowering learners through dynamic visuals and interactivity.

---

An Innovative Way to Teach Mathematics at the Primary Level

1. Bridging Abstract and Concrete Thinking

One of the greatest challenges in primary-level mathematics is helping students transition from concrete thinking (manipulating physical objects) to abstract reasoning (visualizing mathematical relationships). This simulation bridges that gap by:

• Allowing students to construct geometric shapes visually.
• Providing an interactive environment where they can experiment with isometric grids and develop a deeper understanding of 3D shapes.

For example, by recreating a pyramid on the isometric grid, students can visualize how 2D representations correspond to 3D objects, making abstract concepts more accessible.

---

2. Encouraging Active Learning

Traditional teaching methods often rely on static diagrams in textbooks. This simulation introduces hands-on, interactive learning, where:

• Students actively engage with shapes, grids, and spatial reasoning.
• They can self-assess their understanding using the "check" button, promoting self-directed learning and instant feedback.

By moving away from passive learning, the simulation nurtures curiosity and helps students build confidence in their mathematical abilities.

---

3. Promoting Higher-Order Thinking Skills

The simulation encourages students to develop critical thinking and problem-solving skills through:

• Spatial Visualization: Students learn to mentally manipulate shapes and visualize transformations.
• Precision and Accuracy: Reconstructing shapes requires careful alignment and attention to detail.
• Creative Exploration: Teachers can use open-ended tasks, asking students to create their own shapes or design patterns.

These skills are essential for higher-level mathematics and STEM fields, laying a strong foundation for future learning.

---

4. Supporting Differentiated Learning

Every student learns at a different pace, and this simulation accommodates diverse learning needs:

• Scaffolded Learning: Teachers can start with simpler shapes like cubes and progress to more complex ones, such as pyramids, to match the skill level of each student.
• Self-Paced Exploration: Students can explore and practice at their own pace, making it suitable for mixed-ability classrooms.

The visual and interactive nature of the simulation ensures that both visual and kinesthetic learners are engaged effectively.

---

5. Aligning with Modern Pedagogical Practices

The simulation aligns with 21st-century pedagogical practices, which emphasize technology integration and interactive learning environments. Key benefits include:

• Gamification of Learning: Features like the "check" button introduce an element of challenge and fun, motivating students to improve.
• Real-Time Analytics: By embedding tracking tools like Google Tag Manager, teachers can monitor student engagement and tailor lessons accordingly.

---

Key Features of the Simulation

1. Interactive Grid and Shapes

   • A left panel displays 3D shapes (e.g., pyramids and cubes) as base references.
   • A right panel with an isometric grid allows users to recreate the shapes interactively.

2. Dynamic Dropdown Selection

   • Users can toggle between predefined shapes using the dropdown menu. This fosters exploration of various geometric configurations.

3. Clear and Check Options

   • A "clear" button resets the grid for fresh attempts, while the "check" button verifies user inputs against the original shapes.

4. Customizable UI Elements

   • The simulation can integrate user-defined assets (e.g., custom logos) and metadata fields for localization and personalization.

---

Best Practices for EJS Documentation

To maximize usability and scalability of the simulation, it’s crucial to maintain well-structured documentation. Here are recommended steps:

1. Metadata Setup

• Title and Author Information: Clearly define the simulation title (Math_Isometric_Grid_v1) and authorship to credit contributors.
  
  
  
  
  
  
  
  
• Keywords and Comments: Use tags like "geometry," "isometric grid," and "3D modeling" for better discoverability.

2. Instructions for Users

Incorporate clear instructions directly within the simulation or its accompanying documentation:

• Dropdown Menu: Select shapes to practice isometric modeling.
• Interactive Grid: Drag and drop points to construct shapes.
• Verification: Use the "check" button to validate your work.

3. Include a Thumbnail

A 320x180px preview image improves user engagement on platforms like Learning Management Systems (LMS). Ensure the file size is optimized for quick loading without compromising clarity.

 

320x180px preview image

 

4. Embed Tracking Code

For usage analytics, integrate Google Tag Manager (GTM) or similar tools. This helps educators evaluate interaction metrics and student engagement.

https://github.com/lookang/codesforejss/blob/master/Google%20Analytics%20and%20Adsense

5. Use Standardized Assets

Host all required files (e.g., logosometric.png) in accessible paths, and ensure they are properly linked in the "Files required" section of the EJS Run Options.

 

---

Conclusion

The webejs_model_Math_Isometric_Grid_v1 is a groundbreaking tool for teaching mathematics at the primary level. By making abstract geometry concepts tangible and accessible, it fosters an engaging and active learning environment for young learners. Furthermore, its alignment with modern pedagogical practices ensures its relevance and effectiveness in today’s classrooms.

With proper documentation and integration, this simulation has the potential to transform the way mathematics is taught, empowering students with the skills and confidence needed for success.

 

Drawing 3D Shapes on an Isometric Grid: A Fun and Educational Tool

Introduction

Visualizing and drawing 3D shapes can be a challenging yet rewarding task. It’s a great way to improve spatial awareness, logical thinking, and artistic skills. Our interactive tool takes this learning process to the next level by allowing users to choose a 3D shape and replicate it on an isometric grid. This hands-on activity is perfect for students, educators, or anyone interested in exploring 3D geometry.

How It Works

The tool is simple yet powerful, designed to make learning intuitive and engaging. Here's a step-by-step breakdown:

1. Select a Shape:

   • Users start by selecting a 3D shape from a dropdown menu. Options include familiar forms like cubes, cuboids, prisms, pyramids, and more.
   • The selected shape is displayed on the left side of the interface as a reference.

2. Draw on the Isometric Grid:

   • The right side of the interface features an isometric grid, which is perfect for drawing 3D objects.
   • Users click on the grid points to create lines, constructing their interpretation of the displayed shape.

3. Check Your Work:

   • Once the drawing is complete, users can click the "Check" button to verify their creation against the reference shape.
   • Feedback is provided to help users refine their understanding and improve their accuracy.

4. Clear and Retry:

   • If a user wants to start over, they can simply hit the "Clear" button to reset the grid and try again.

Educational Benefits

This tool offers numerous educational advantages:

• Improves Spatial Reasoning: Drawing 3D shapes on a 2D grid helps users understand depth, perspective, and spatial relationships.
• Enhances Problem-Solving Skills: Users must think critically about how to represent complex 3D forms using simple lines and points.
• Encourages Creativity: The isometric grid can also be used to create custom shapes or designs beyond the provided examples.
• Interactive Learning: The hands-on nature of the tool keeps users engaged and motivated.

Use Cases

1. Classroom Learning:
   • Teachers can use this tool as part of a geometry lesson, challenging students to draw various 3D shapes.
2. Art and Design:
   • Aspiring designers and artists can use the grid to practice isometric drawing techniques.
3. Recreational Use:
   • Puzzle enthusiasts and hobbyists can enjoy the challenge of recreating shapes or designing their own.

Conclusion

Our isometric drawing tool bridges the gap between 2D and 3D learning, making it easier to understand complex geometric concepts. Whether you're a student, teacher, or simply someone who loves a good challenge, this tool offers a fun and interactive way to explore the world of 3D shapes. Try it out and see how quickly your spatial reasoning and artistic skills improve!

 Version:

1. https://weelookang.blogspot.com/2024/12/drawing-3d-shapes-on-isometric-grid-fun.html 
2. https://weelookang.blogspot.com/2024/12/exploring-math-isometric-grid.html 

Other Resources

[text]