.png
)
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits
This email address is being protected from spambots. You need JavaScript enabled to view it.; Francisco Esquembre; Felix J. Garcia Clemente
Learning Goals
2019 PSLE Question on finding Diameter
Method 1 by the Boring physics teacher https://youtu.be/JuGNaORvxvs
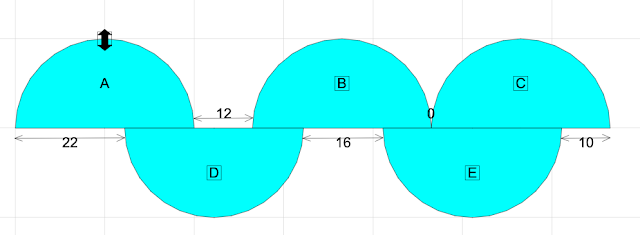
Shift circle C by 12 cm. Therefore, by symmetry looking at the circle B, the diameter is 10+16+10 where 10 is from the shifting of 22-12, the first 10 is by symmetry. The diameter is 36 cm.
Method 2 by Julie Choy
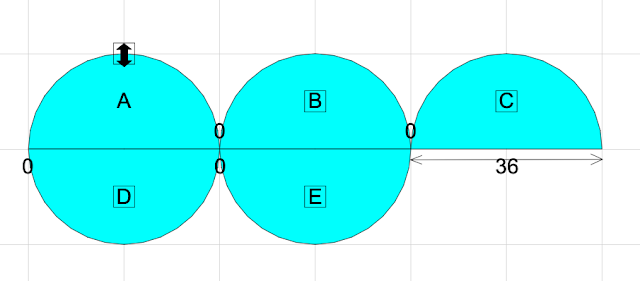
Shift circle B, C, D and E to the extreme left to align them up. So, the circle C is the odd one out. Then the diameter is sum of the bottom numbers subtract the sum of the top numbers, leading to 22+16+22 - (12+12) =36 cm.
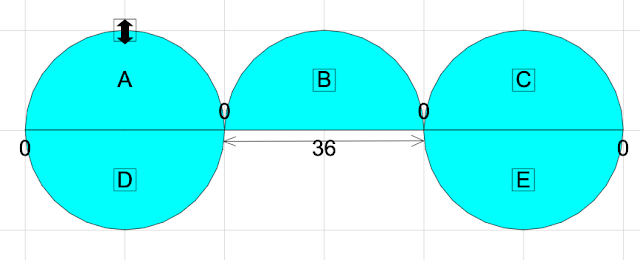
Method 3
Shift circle D to the extreme left align with circle A. Shift circle E to the extreme right align with circle C. So, the bottom numbers add up is equal to the 2 top numbers plus diameter B. Therefore, the diameter is sum of the bottom numbers subtract the sum of the top numbers, leading to 22+16+22 - (12+12) =36 cm.
Conclusion
Therefore, the principle to solving this kind of problem is to look out for a pattern that leads to top set of numbers - bottom set of numbers, is the odd length out which is the diameter in this case.
For Teachers
[text]
Research
[text]
Video
[text]
Version:
Other Resources
[text]
end faq
{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}
- Details
- Written by Loo Kang Wee
- Parent Category: geometry
- Category: 1. 2D Shapes
- Hits: 4392