About

Geometric sequence and its series

The members of the geometric sequence follow the rule:

x_i+1= x_i*a

x_i it the i-th member of the sequence, with index i a positive integer, including 0. The growth parameter a is real number. With

x₀=1

the members are 1, a, a², a³, a⁴..... x_i =a ⁱ

The geometric series (sequence of partial sums) is generated by consecutive addition of the members of the geometric sequence:  The partial sums are:

S_i = Σ_oⁱ a ⁿ with 0 ≤ n≤ i; S_i = 1 + a + a ²....+a ⁱ

In the simulation you can vary parameter a by a slider in the range -1,05≤ a ≤+1,05 . Reset returns to the default value 0.5 .

The interesting issue is if the series will have a finite value (a limit, if the series is convergent) when the index grows unlimited, or if it goes to infinity (the series is divergent). This depends on a.

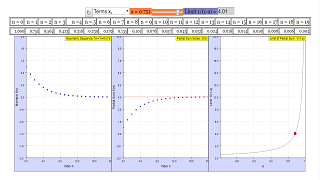
The left chart displays the members of the sequence, while the middle chart those of the partial sum series, both in dependence on the index n. On the right, the chart of the limit of the series of partial sums is shown in dependence on a, with a red point for its chosen value.

The values for each term can be viewed in the table above the graphs. You can toggle between viewing the individual terms of the sequence or the partial sum of the series using the combobox provided.

When a is smaller than 1 the geometric series of partial sums converges to

limitS _i = 1 / (1-a) for abs(a) < 1

The graph in the right window displays this formula for the range

-0.98 < a < 0.98

.

E1: Reset to a = 0.5

The partial sum series converges to 2.

How does the sequence evolve?

Try mentally to explain to a child how summing infinite finite numbers, none of which has a zero value, can lead to a finite value!

E2: Choose a around + 1

Obviously convergence of the partial sums needs a < 1.

What is the condition for the members of the sequence?

E3: Choose a < 1.

Compare sequence and series.

E4: Observe the red point in the limit window and compare with the series charts.

E4: Imagine: a = 0.5 . Now 10, 1000, 1000000 members of another sequence with increasing member value, whose respective sum is 50, 1000000, 10¹² is added to the geometric series. Will the total sum be convergent? If yes, what is its limit?

E5: Which range of the index decides if an arbitrary series with finite members is convergent or not?

This file was created in August 2008 by Dieter Röß

This simulation is part of

“Learning and Teaching Mathematics using Simulations

– Plus 2000 Examples from Physics”

ISBN 978-3-11-025005-3, Walter de Gruyter GmbH & Co. KG

 

Translations

Code	Language		Translator	Run

Credits

Dieter Roess - WEH- Foundation; Tan Wei Chiong; Loo Kang Wee

1. Introduction:

This briefing document reviews the provided excerpts detailing a JavaScript simulation applet focused on geometric sequences and series. The applet, developed using HTML5, is designed as an open educational resource for learning and teaching mathematics, particularly within the context of simulations. This document outlines the core concepts addressed by the simulation, its features, and its intended educational applications.

2. Main Themes and Important Ideas/Facts:

The primary focus of this resource is to illustrate and explore the properties of geometric sequences and their corresponding series (partial sums). Key concepts highlighted include:

• Definition of a Geometric Sequence: The resource clearly defines a geometric sequence as a sequence where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio. The formula provided is: "xi+1= xi * a", where xi is the i-th member and a is the growth parameter (common ratio). With the initial term x0 set to 1, the sequence takes the form: 1, a, a², a³, ... , ai.
• Definition of a Geometric Series: A geometric series is defined as the sum of the terms in a geometric sequence. The formula for the partial sum Si up to the i-th term is given as: "Si = Σoia n with 0 ≤ n≤ i; Si = 1 + a + a²....+a i".
• Convergence and Divergence of Geometric Series: A central theme is the behavior of the geometric series as the number of terms increases indefinitely. The resource explicitly states that the convergence of the series (having a finite limit) or divergence (going to infinity) depends on the value of the common ratio, a. "The interesting issue is if the series will have a finite value (a limit, if the series is convergent) when the index grows unlimited, or if it goes to infinity (the series is divergent). This depends on *a* ."
• Condition for Convergence: The document clearly states the condition for the convergence of a geometric series: "When *a* is smaller than 1 the geometric series of partial sums converges to limitS i *= 1 / (1-a) for abs(a) < 1". This is a fundamental concept in the study of series.
• Simulation Features: The JavaScript applet offers several interactive features to aid understanding:
• Slider for Parameter 'a': Users can dynamically change the common ratio (a) within the range of -1.05 to +1.05 using a slider. The "Reset" button sets the default value to 0.5.
• Multiple Charts: The simulation provides three graphical representations:
• The left chart displays the individual terms of the geometric sequence against the index n.
• The middle chart shows the partial sums of the series against the index n.
• The right chart plots the limit of the series of partial sums as a function of a, with a "red point for its chosen value."
• Data Table: A table above the graphs displays the numerical values of each term, allowing for precise observation.
• Combobox for Viewing: Users can toggle between viewing the individual terms of the sequence or the partial sums of the series.
• Limit Display: The field next to the slider displays the calculated limit of the sum using the formula 1/(1-a) for |a|<1.
• Experiments for Exploration: The resource includes a section titled "Experiments" with specific tasks designed to guide learning:
• E1 (Reset to a = 0.5): Focuses on observing the convergence of the series to 2 and prompting reflection on how an infinite sum of non-zero numbers can be finite. "Try mentally to explain to a child how summing infinite finite numbers, none of which has a zero value, can lead to a finite value!"
• E2 (Choose 'a' around +1): Emphasizes the condition for convergence (a < 1).
• E3 (Choose 'a' < 1): Encourages comparison between the behavior of the sequence and the series.
• E4 (Observe the red point): Directs users to connect the limit displayed in the right window with the partial sum behavior in the middle chart.
• E5 (Imagine adding another sequence): Explores the impact of adding terms from a potentially divergent sequence to a convergent geometric series, implicitly questioning the conditions for overall convergence. "Will the total sum be convergent? If yes, what is its limit?"
• E6 (Which range of the index decides convergence?): This question prompts deeper thinking about the long-term behavior of series and the role of infinite terms in determining convergence.
• Educational Purpose: The applet is explicitly designed for "Learning and Teaching Mathematics using Simulations". The inclusion of "Sample Learning Goals" and a "For Teachers" section further reinforces this purpose.
• Connection to Physics: The simulation is part of a larger collection titled "Learning and Teaching Mathematics using Simulations – Plus 2000 Examples from Physics," suggesting an interdisciplinary approach to learning mathematical concepts.
• Attribution and Licensing: The resource clearly identifies the authors and contributors and specifies the licensing under the Creative Commons Attribution-Share Alike 4.0 Singapore License. It also provides information regarding commercial use of the underlying EasyJavaScriptSimulations Library.

3. Intended Use and Pedagogical Value:

This simulation applet offers a valuable tool for educators and students to:

• Visualize Abstract Concepts: The graphical representations of the geometric sequence, partial sums, and the limit provide a visual and intuitive understanding of these abstract mathematical concepts.
• Explore the Effect of Parameters: The interactive slider allows students to experiment with different values of the common ratio (a) and observe the immediate impact on the sequence and series behavior, fostering a deeper understanding of the convergence condition.
• Conduct Guided Inquiry: The "Experiments" section provides structured activities that encourage students to explore the properties of geometric sequences and series through observation and reflection.
• Facilitate Conceptual Understanding: By visualizing the summation process and the concept of a limit, the simulation can help students grasp why an infinite sum can converge to a finite value under certain conditions.
• Support Interdisciplinary Learning: The connection to physics examples suggests potential applications in modeling physical phenomena that exhibit geometric growth or decay.

4. Potential Limitations and Considerations:

• The simulation, as described, focuses on geometric sequences with the first term x0 set to 1. While this simplifies the initial introduction, it might be beneficial to explore cases with different starting terms.
• The range of the slider for a is limited to -1.05 to +1.05. While this covers the critical region around -1 and 1, expanding it slightly might allow for further exploration of divergent cases.
• The level of mathematical rigor in the provided excerpts is introductory. For more advanced learners, further theoretical explanations might be necessary to complement the simulation.

5. Conclusion:

The Geometric Sequence and Series JavaScript Simulation Applet HTML5 is a well-designed and pedagogically sound open educational resource. Its interactive features, clear visualizations, and guided experiments provide an effective way for students to learn and explore the fundamental concepts of geometric sequences and series, particularly the crucial idea of convergence. The applet's accessibility through HTML5 and its open licensing further enhance its value for the educational community.

 

Geometric Sequences and Series Study Guide

Key Concepts

• Geometric Sequence: A sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio (a in this context). The general form is 1, a, a², a³, ... where the first term (x₀) is 1.
• Common Ratio (a): The constant factor by which each term in a geometric sequence is multiplied to obtain the next term. In the simulation, this parameter can be varied using a slider.
• Geometric Series: The sum of the terms of a geometric sequence. The partial sums (Sᵢ) are the sum of the first i+1 terms: Sᵢ = 1 + a + a² + ... + aⁱ.
• Partial Sum: The sum of a finite number of consecutive terms of a sequence. For a geometric series, Sᵢ represents the partial sum of the first i+1 terms.
• Convergence: A property of an infinite series where the sequence of its partial sums approaches a finite limit as the number of terms increases indefinitely.
• Divergence: A property of an infinite series where the sequence of its partial sums does not approach a finite limit, often growing indefinitely.
• Limit of a Convergent Geometric Series: When the absolute value of the common ratio is less than 1 (|a| < 1), the infinite geometric series converges to a finite limit given by the formula: Limit (Sᵢ) = 1 / (1 - a).
• Simulation Interface: The interactive applet displays three charts: the geometric sequence terms, the partial sums of the series, and the limit of the series as a function of the common ratio (a). A slider allows for varying a, a reset button returns to the default a = 0.5, and a combobox toggles between viewing sequence terms and partial sums in a table.

Short-Answer Quiz

1. What defines a geometric sequence, and what is the specific rule for generating terms in the sequence presented in the simulation?
2. Explain the relationship between a geometric sequence and a geometric series. How are the partial sums of a geometric series calculated?
3. What is the significance of the growth parameter 'a' in the context of a geometric sequence and its corresponding series, and what is its default value in the simulation?
4. Describe the visual representation provided by the three charts in the simulation applet and what each chart displays in relation to geometric sequences and series.
5. Under what condition does a geometric series converge to a finite value as the number of terms approaches infinity, and what is the formula for this limit?
6. What does it mean for a series to be divergent, and how does the value of the common ratio 'a' influence whether a geometric series converges or diverges?
7. Explain the functionality of the slider and the reset button in the simulation applet, and how they allow for exploration of geometric sequences and series.
8. What information can be viewed in the table above the graphs in the simulation, and how can the combobox be used to change this displayed information?
9. According to Experiment E1, when 'a' is 0.5, the partial sum series converges to 2. Describe how the individual terms of the sequence evolve in this scenario.
10. According to the source material, what is the formula displayed in the right window of the simulation for the limit of the series of partial sums, and for what range of 'a' is this formula applicable in the graph?

Answer Key

1. A geometric sequence is a sequence where each term is found by multiplying the previous term by a constant common ratio. In the simulation, with the first term x₀ = 1, the rule is xᵢ₊₁ = xᵢ * a, resulting in the sequence 1, a, a², a³, ....
2. A geometric series is the sum of the terms in a geometric sequence. The partial sums of a geometric series are calculated by consecutively adding the members of the geometric sequence: Sᵢ = 1 + a + a² + ... + aⁱ.
3. The growth parameter 'a' (the common ratio) determines how the terms of the geometric sequence change and whether the corresponding series converges or diverges. Its default value in the simulation is 0.5.
4. The leftmost chart displays the individual members of the geometric sequence versus the index 'n'. The middle chart shows the partial sums of the series versus 'n'. The rightmost chart plots the limit of the series of partial sums as a function of 'a', with a red point indicating the limit for the chosen 'a' value.
5. A geometric series converges to a finite value when the absolute value of the common ratio 'a' is less than 1 (|a| < 1). The formula for this limit is Limit (Sᵢ) = 1 / (1 - a).
6. A series is divergent when its sequence of partial sums does not approach a finite limit as the number of terms increases. If the absolute value of 'a' is greater than or equal to 1 (|a| ≥ 1), the geometric series will diverge.
7. The slider allows the user to change the value of the common ratio 'a' within the range of -1.05 to +1.05. The reset button sets the value of 'a' back to its default value of 0.5.
8. The table above the graphs displays the numerical values of either the individual terms of the geometric sequence or the partial sums of the series, depending on the selection made in the combobox.
9. When 'a' is 0.5, the sequence evolves such that each term is half of the previous term (1, 0.5, 0.25, 0.125, and so on), approaching zero as the index grows.
10. The formula displayed in the right window for the limit of the series of partial sums is Limit Sᵢ = 1 / (1 - a). The graph in the right window displays this formula for the range -0.98 < a < 0.98.

Essay Format Questions

1. Discuss the relationship between the value of the common ratio (a) and the convergence or divergence of an infinite geometric series. Use examples from the simulation to illustrate your points.
2. Explain how the simulation visually represents the concept of a geometric sequence, its partial sums, and the limit of the corresponding infinite series. Describe how interacting with the simulation can enhance understanding of these concepts.
3. Consider Experiment E4. Analyze whether adding a sequence with increasing member values to a convergent geometric series will always result in a divergent total sum. Justify your answer with reasoning based on the principles of convergence.
4. Explain the counterintuitive idea that summing infinitely many finite, non-zero numbers can result in a finite value, as demonstrated by convergent geometric series. Use the simulation with a specific value of 'a' to support your explanation.
5. Compare and contrast the behavior of a geometric sequence and its corresponding geometric series as the number of terms increases, considering different values of the common ratio (a). How does the simulation help to visualize these differences?

Glossary of Key Terms

• Geometric Sequence: An ordered list of numbers where the ratio between any two successive members of the sequence is constant.
• Geometric Series: The sum of the terms of a geometric sequence, which can be finite (partial sum) or infinite.
• Common Ratio: The constant factor used to multiply each term in a geometric sequence to get the next term. Denoted as 'a' in the provided source.
• Term: Each individual number in a sequence. In the geometric sequence here, the i-th term is denoted as xᵢ.
• Index: The position of a term within a sequence, starting from 0 (as indicated by i in xᵢ).
• Partial Sum (Sᵢ): The sum of the first i+1 terms of a sequence. For a geometric series starting with 1, Sᵢ = 1 + a + a² + ... + aⁱ.
• Convergence: The property of an infinite series to approach a specific, finite value as more terms are added.
• Divergence: The property of an infinite series to not approach a specific, finite value as more terms are added; often the sum grows indefinitely.
• Limit: The value that a sequence or series approaches as the number of terms increases without bound. For a convergent geometric series with |a| < 1, the limit is 1 / (1 - a).
• Growth Parameter: Another term for the common ratio (a), highlighting its role in determining the growth or decay of the terms in the geometric sequence.
• Slider: An interactive user interface element that allows continuous adjustment of a parameter's value (in this case, the common ratio 'a').
• Reset: A function that returns a parameter to its original or default value (here, setting 'a' back to 0.5).
• Combobox: An interactive user interface element that presents a dropdown list of options from which a user can select (in this case, to view either the sequence terms or the partial sums in the table).

Sample Learning Goals

[text]

For Teachers

A geometric sequence is a number sequence of the form
,
where a is the first term of the sequence, and r is a constant, also called the common ratio.

On the other hand, a geometric series is written as the sum of the terms in the sequence as such:
,
where the terms of the sum continue indefinitely.

This simulation sets the first term of the sequence to be 1, and the common ratio in the simulation is denoted as a. From here on, a will denote the common ratio used in the simulation.

There are 3 graphs in the simulation. The leftmost graph plots the first 20 terms of the geometric sequence, the center graph plots the partial sum of those 20 terms, and the rightmost graph plots the limit of the series as the common ratio achanges.
The red arrow in the center graph denotes the limit of the partial sums as the number of terms approach infinity.

The common ratio, a, can be changed using the slider at the top of the simulation, and the field to the right of the slider displays the limit that the sum approaches (1/(1-a) for |a|<1).

The combo box allows you to toggle the array display between showing the terms of the sequence and the partial sums up to a certain term.

Research

[text]

Video

[text]

 Version:

1. http://weelookang.blogspot.sg/2016/02/vector-addition-b-c-model-with.html improved version with joseph chua's inputs
2. http://weelookang.blogspot.sg/2014/10/vector-addition-model.html original simulation by lookang

Other Resources

[text]

What is a geometric sequence?

A geometric sequence is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio. In this simulation, with the first term (x₀) set to 1, the sequence is defined by the rule xᵢ₊₁ = xᵢ * a, where 'a' is the common ratio. This generates a sequence like 1, a, a², a³, and so on, where the i-th member is aⁱ.

What is a geometric series?

A geometric series is the sum of the terms in a geometric sequence. It is represented as the sequence of partial sums, where each partial sum (Sᵢ) is the sum of the first i+1 terms of the geometric sequence. Mathematically, Sᵢ = Σ₀ⁱ aⁿ = 1 + a + a² + ... + aⁱ.

What does the simulation allow you to do?

The JavaScript simulation allows users to explore geometric sequences and series interactively. You can vary the common ratio ('a') using a slider within the range of -1.05 to +1.05. The simulation visually displays three charts: the terms of the geometric sequence, the partial sums of the series, and the limit of the series of partial sums as 'a' changes. You can also view the numerical values of the terms and partial sums in a table and toggle between them using a combobox. Resetting the simulation returns 'a' to its default value of 0.5.

What determines if a geometric series converges or diverges?

Whether a geometric series has a finite value (converges) or goes to infinity (diverges) as the number of terms increases infinitely depends on the value of the common ratio ('a').

Under what condition does a geometric series converge and what is its limit?

A geometric series converges to a finite limit when the absolute value of the common ratio 'a' is less than 1 (|a| < 1). In this case, the limit of the series (S) is given by the formula: S = 1 / (1 - a). The simulation's rightmost graph displays this limit for the range -0.98 < a < 0.98.

What happens to the geometric sequence and series when 'a' is around +1 or less than 1?

When the common ratio 'a' is around +1, the terms of the geometric sequence remain relatively constant or increase slowly, but the partial sums of the series will generally not converge to a finite limit (as convergence requires a < 1). When 'a' is less than 1, the terms of the geometric sequence will decrease in magnitude (approaching zero if |a| < 1), and the geometric series of partial sums will converge to the limit 1 / (1 - a).

According to Experiment E4, if another sequence with increasing member values and increasing sums is added to a convergent geometric series, will the total sum remain convergent?

No, if a sequence with increasing member values (and thus increasing partial sums) is added to a convergent geometric series, the total sum will not remain convergent. The increasing values of the added sequence will cause the overall sum to grow without bound, resulting in a divergent series. The convergence of the original geometric series depends on its terms becoming sufficiently small, which will be counteracted by the increasing terms of the added sequence.

According to Experiment E5, which range of the index decides if an arbitrary series with finite members is convergent or not?

The convergence or divergence of an arbitrary infinite series with finite members is determined by the behavior of its terms as the index approaches infinity. The initial, finite number of terms does not affect the ultimate convergence. Convergence depends on whether the terms eventually become sufficiently small (approaching zero fast enough) such that the sum approaches a finite limit as the number of terms goes to infinity.