About

The Mandelbrot set

The Mandelbrot set consists of points, c, in the complex plane that obey the following rule

1. Start with the complex number z = a + ib where a and b are real numbers.
2. Generate a new complex number, z', by multiplying z by itself and adding the result to c. z' = z² + c.
3. Repeat steps 1 and 2. If the complex number z goes toward infinity, then the starting point, c, is not a member of the Mandelbrot set. All numbers that remain bounded are members of the set.

It can be shown that if the magnitude of z is greater than 2 , then z will approach infinity. The code assumes that the number c is in the set if |z| > 2 after 256 iterations. In order to show how rapidly a number fails the test, we color the pixel corresponding to the number of iterations.

 

Mandelbrot set

The members of the Mandelbrot set follow the rule

z_n+1= z_n²+ c ; z₀ = 0

c is a complex number, as is z

We look for points c in the complex plane, for which the sequence does not diverge. They form the Mandelbrot set. In the simulation they are colored red, lying within a range with fractal boundary, the famous "apple man". Diverging points are colored green to blue, with the color shading indicating the speed of divergence.

Drawing a rectangle with the mouse defines a smaller range of calculation with correspondingly increasing resolution. Reset leads back to the initial condition.

The series has the members 0, c, c²+ c, c⁴ + 2c³ + c² + c,...

The fractal structure is caused by the nonlinearity of the sequence rule. It is observed for other nonlinear sequences as well, with different structure of the fractal.

Julia set

The Julia set corresponding to the Mandelbrot set is generated with the same rule : z_n+1=z_n²+c. Yet with the Julia set c is constant, and we calculate for which point z of the complex plane the sequence converges to a finite non zero value. Each point c of the complex plane has its own Julia set. In the chart with the Mandelbrot set you see a white point that defines c. It can be drawn with the mouse. The right chart displays the corresponding Julia set. Again a calculation range with higher resolution can be defined by drawing a rectangle with the mouse. Reset at the Julia chart leads back to the Julia range for the given magnification in the Mandelbrot chart. Reset at the Mandelbrot chart leads back to the Julia set with c = 0 at the original size of the Mandelbrot set. The Julia set are points at the fractal border. The degree of divergence or convergence to zero is indicated by color shading. Its gradation can be changed by a slider, which produces interesting color schemes. The connection between a basic fractal and its Julia set are similar with different set rules.

Julia set

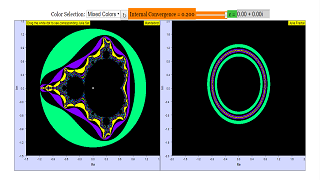
When opening the simulation or at Reset at the chart of the Julia set you see the unit circle surrounded inside and outside by circular blue shaded areas.

The green rim of the unit circle is the Julia set of the white point c = (0,0) in the plane of the Mandelbrot chart. Color shading indicates how fast points outside diverge and points inside converge to zero. The criterion of inside shading can be adjusted with the slider (higher value for less differentiation).

For all points c the Julia set is the green rim of the fractal. Blue areas are those of fast, red those of slow divergence or convergence to zero, and do not belong to the set. The slider varies the gradation of shading. This gives additional insight into the convergence landscape and increases the aesthetic beauty of the fractal structures. Shift the slider at high resolution!

Most impressive large scale structures are calculated for points at the rim or outside of the Mandelbrot fractal. Yet at high resolution the apparently simple structure for points inside reveals interesting fine structure, recalling that of coastal lines or of natural surfaces.

e_Julia_Set.ejss is developed by Loo Kang Wee and Wei Chiong Tan based on the works of eariler authors below. mandelbrot.xml was originally developed by Francisco Esquembre and Wolfgang Christian The Julia- version was developed by Dieter Roess in October 2008 This simulation is part of the work “Learning and Teaching Mathematics using Simulations – Plus 2000 Examples from Physics” ISBN 978-3-11-025005-3, Walter de Gruyter GmbH & Co. KG

This simulation is part of

“Learning and Teaching Mathematics using Simulations

– Plus 2000 Examples from Physics”

ISBN 978-3-11-025005-3, Walter de Gruyter GmbH & Co. KG

 

Translations

Code	Language		Translator	Run

Credits

Dieter Roess - WEH- Foundation; Tan Wei Chiong; Loo Kang Wee; Francisco Esquembre ; Wolfgang Christian

Overview:

This document provides a briefing on the Mandelbrot and Julia sets as described within the Open Educational Resources / Open Source Physics @ Singapore website. The source focuses on a JavaScript simulation applet that allows users to interactively explore these fascinating mathematical concepts. The briefing will cover the definitions of both sets, their generation processes, their visual representation in the simulation, and the pedagogical value highlighted by the resource.

Main Themes and Important Ideas/Facts:

1. Definition and Generation of the Mandelbrot Set:

• Core Rule: The Mandelbrot set is defined by complex numbers, denoted as c, for which the iterative sequence zn+1 = zn2 + c, with the initial value z0 = 0, does not diverge to infinity.
• Quote: "The Mandelbrot set consists of points, c , in the complex plane that obey the following rule: 1. Start with the complex number z = a + ib where a and b are real numbers. 2. Generate a new complex number, z' , by multiplying z by itself and adding the result to c . z' = z2 + c. 3. Repeat steps 1 and 2. If the complex number z goes toward infinity, then the starting point, c , is not a member of the Mandelbrot set. All numbers that remain bounded are members of the set."
• Quote: "The members of the Mandelbrot set follow the rule zn+1= zn2 + c ; z0 = 0. c is a complex number, as is z. We look for points c in the complex plane, for which the sequence does not diverge. They form the Mandelbrot set."
• Divergence Test: The simulation uses the criterion that if the magnitude of z exceeds 2 after a certain number of iterations (assumed to be 256 in the code), then c is considered to be outside the Mandelbrot set and the sequence will approach infinity.
• Quote: "It can be shown that if the magnitude of z is greater than 2 , then z will approach infinity. The code assumes that the number c is in the set if |z| > 2 after 256 iterations."
• Visual Representation: Points within the Mandelbrot set are typically colored red in the simulation, forming the characteristic "apple man" shape with a fractal boundary. Points outside the set are colored green to blue, with the color indicating the speed of divergence.
• Quote: "In the simulation they are colored red, lying within a range with fractal boundary, the famous 'apple man'. Diverging points are colored green to blue, with the color shading indicating the speed of divergence."
• Fractal Nature: The boundary of the Mandelbrot set exhibits fractal properties, meaning that zooming into the boundary reveals repeating patterns of increasing complexity.
• Quote: "The fractal structure is caused by the nonlinearity of the sequence rule. It is observed for other nonlinear sequences as well, with different structure of the fractal."
• Quote: "The shape formed by the Mandelbrot Set is also a fractal, where zooming in to the boundary of the shape formed by the set reveals repeating patterns of equal or increasing complexity as the magnification increases."
• Interactive Exploration: The simulation allows users to define a smaller range of calculation by drawing a rectangle with the mouse, which increases the resolution and enables exploration of the intricate details of the fractal. The "Reset" button returns to the initial view.

2. Definition and Generation of the Julia Set:

• Core Rule: The Julia set is generated using the same iterative rule, zn+1 = zn2 + c, but with a fixed complex number c. The iteration is then performed for different starting points z in the complex plane to determine which points converge to a finite non-zero value.
• Quote: "The Julia set corresponding to the Mandelbrot set is generated with the same rule : zn+1=zn2 +c. Yet with the Julia set c is constant, and we calculate for which point z of the complex plane the sequence converges to a finite non zero value."
• Dependence on c: Each point c in the complex plane has its own unique Julia set.
• Quote: "Each point c of the complex plane has its own Julia set."
• Connection to Mandelbrot Set: The simulation visually links the Mandelbrot set and the Julia set. A white point on the Mandelbrot set, selectable by the user, defines the constant c for the Julia set displayed in the adjacent chart.
• Quote: "In the chart with the Mandelbrot set you see a white point that defines c. It can be drawn with the mouse. The right chart displays the corresponding Julia set."
• Visual Representation: The Julia set itself forms the fractal border. Points whose iterations diverge or converge to zero are colored blue (fast) or red (slow), indicating they do not belong to the set.
• Quote: "The Julia set are points at the fractal border. The degree of divergence or convergence to zero is indicated by color shading. Its gradation can be changed by a slider , which produces interesting color schemes."
• Interactive Exploration: Similar to the Mandelbrot set, users can draw a rectangle on the Julia set chart to increase resolution. "Reset" on the Julia chart returns to the magnified view corresponding to the Mandelbrot chart, while "Reset" on the Mandelbrot chart reverts the Julia set to the case where c = 0 at the initial zoom level.
• Example with c = (0,0): The simulation initializes the Julia set with c = (0,0), resulting in the unit circle as the Julia set, with internal and external areas shaded blue based on the speed of convergence to zero or divergence.
• Quote: "When opening the simulation or at Reset at the chart of the Julia set you see the unit circle surrounded inside and outside by circular blue shaded areas. The green rim of the unit circle is the Julia set of the white point c = (0,0) in the plane of the Mandelbrot chart. Color shading indicates how fast points outside diverge and points inside converge to zero."
• Slider for Color Gradation: A slider allows users to adjust the gradation of color shading in the Julia set, providing additional insight into the convergence landscape and enhancing the visual aesthetics.
• Quote: "The slider varies the gradation of shading. This gives additional insight into the convergence landscape and increases the aesthetic beauty of the fractal structures. Shift the slider at high resolution!"

3. Pedagogical Value and Features of the Simulation:

• Learning Mathematics through Simulation: The resource is part of a larger project focused on using simulations for learning and teaching mathematics.
• Quote: "This simulation is part of 'Learning and Teaching Mathematics using Simulations – Plus 2000 Examples from Physics' ISBN 978-3-11-025005-3, Walter de Gruyter GmbH & Co. KG"
• Interactive Exploration: The JavaScript applet provides an interactive way for students to visualize and understand the abstract concepts of complex numbers, iteration, convergence, divergence, and fractals.
• Visual Connection: The side-by-side display of the Mandelbrot set and its corresponding Julia set helps users grasp the relationship between these two concepts.
• Adjustable Parameters: The ability to select the c value for the Julia set and adjust the color shading offers opportunities for experimentation and deeper understanding.
• Embeddable Model: The simulation can be easily embedded into web pages using an iframe.
• Quote: "Embed this model in a webpage: <iframe width="100%" height="100%" src="https://iwant2study.org/lookangejss/math/Series_Numbers/ejss_model_e_Julia_Set/e_Julia_Set_Simulation.xhtml " frameborder="0">"
• Sample Learning Goals: The resource includes a section outlining sample learning goals for the simulation (although the specific text is not provided in the excerpt).
• For Teachers: The resource explicitly states that the simulation is of a Mandelbrot Set along with its corresponding Julia Set, providing context for educators.

4. Technical Details and Credits:

• Developed using Easy JavaScript Simulation (EJS): The applet was created using the EJS framework.
• Authors and Contributors: The page credits several individuals involved in the development of the simulation, including Loo Kang Wee, Wei Chiong Tan, Francisco Esquembre, Wolfgang Christian, and Dieter Roess.
• Open Educational Resource: The resource is presented as an Open Educational Resource, with content licensed under the Creative Commons Attribution-Share Alike 4.0 Singapore License.

Key Takeaways:

• The Mandelbrot set comprises complex numbers c for which the iterative sequence zn+1 = zn2 + c (with z0 = 0) remains bounded.
• Julia sets are generated by the same iterative rule but with a fixed c, and the behavior of different starting z values is analyzed. Each c corresponds to a unique Julia set.
• The simulation provides a visual and interactive platform to explore the intricate and fractal nature of both sets and their interrelationship.
• Color shading in the simulation effectively conveys the speed of divergence or convergence of the iterative sequences.
• The resource highlights the potential of simulations in enhancing the learning and teaching of complex mathematical concepts.

This briefing document summarizes the key information presented in the provided source regarding the Mandelbrot and Julia sets JavaScript simulation. It emphasizes the mathematical definitions, the simulation's functionality, and its educational value.

 

Study Guide: Mandelbrot and Julia Sets

Key Concepts:

• Complex Numbers: Numbers of the form a + ib, where a and b are real numbers and i is the imaginary unit (√-1).
• Iteration: The process of repeatedly applying a function to an initial value.
• Bounded Sequence: A sequence whose terms do not grow indefinitely large in magnitude.
• Divergent Sequence: A sequence whose terms grow indefinitely large in magnitude.
• Fractal: A self-similar geometric shape whose parts exhibit the same statistical character at many scales.
• Complex Plane: A plane where the horizontal axis represents the real part of a complex number and the vertical axis represents the imaginary part.

Quiz:

1. Describe the fundamental difference in how the Mandelbrot set and the Julia set are generated using the recursive formula zn+1 = zn² + c.
2. What is the initial value of z (z₀) used when determining if a complex number c belongs to the Mandelbrot set? Explain the condition for c to be considered a member.
3. For the Julia set, what is kept constant and what varies across the complex plane? What determines whether a point belongs to a specific Julia set?
4. Explain the significance of the magnitude of z exceeding 2 in the context of the Mandelbrot set iteration. What happens to the sequence if this condition is met?
5. How is the behavior of points (whether they diverge or remain bounded) visually represented in the Mandelbrot and Julia set simulations? What does the coloring typically indicate?
6. What is the role of the "Reset" button in the Mandelbrot set simulation, and how does it affect the displayed view and the parameters of the calculation?
7. Explain how drawing a rectangle with the mouse on either the Mandelbrot or Julia set chart affects the subsequent calculation and the displayed image.
8. Describe the Julia set associated with the white point c = (0,0) in the Mandelbrot chart as described in the text. What do the different colors within and around this set represent?
9. What causes the fractal structure observed in the Mandelbrot and Julia sets, according to the provided text? Is this phenomenon unique to these sets?
10. How does the "slider" in the Julia set simulation affect the visual representation of the set? What kind of insights can adjusting the slider provide?

Answer Key:

1. In the Mandelbrot set generation, the initial value of z is fixed at 0, and we iterate the formula zn+1 = zn² + c for different values of c to determine if they belong to the set. For the Julia set, the value of c is fixed, and we iterate the formula for different starting values of z to see if they belong to that specific Julia set.
2. The initial value of z (z₀) is defined as 0 for the Mandelbrot set. A complex number c is a member of the Mandelbrot set if the magnitude of z in the iterative sequence zn+1 = zn² + c remains bounded (does not tend towards infinity).
3. For a specific Julia set, the complex number c in the formula zn+1 = zn² + c is held constant. The simulation then calculates the behavior of the sequence for various starting points z in the complex plane. A point z belongs to that Julia set if its sequence converges to a finite non-zero value (or, in some definitions related to the border, exhibits bounded behavior).
4. If the magnitude of z exceeds 2 during the Mandelbrot set iteration, it can be mathematically proven that the sequence will approach infinity. Therefore, if |z| > 2 at any point in the iteration (within a set number of iterations, like 256 in the code), the starting point c is not a member of the Mandelbrot set.
5. Points whose corresponding sequences diverge are typically colored in shades of green to blue, with the specific shade often indicating the speed of divergence (how quickly |z| > 2). Points that remain bounded (for the Mandelbrot set) or converge (for the Julia set) are often colored red or lie within the fractal boundary.
6. The "Reset" button in the Mandelbrot set simulation returns the view to the initial conditions, which includes the original range of calculation and resolution. This effectively zooms out to the initial view of the Mandelbrot set.
7. Drawing a rectangle with the mouse on either chart defines a smaller region of the complex plane for calculation. This action increases the resolution of the displayed image within that selected region, allowing for a closer examination of the fractal details.
8. When opening the simulation or resetting the Julia set chart, and the white point c = (0,0) in the Mandelbrot chart, the Julia set is the green rim of the unit circle in the complex plane. The blue shaded areas inside and outside the circle represent points where the sequence diverges or converges to zero quickly, while red areas indicate slower divergence or convergence.
9. The fractal structure of the Mandelbrot and Julia sets is caused by the nonlinearity of the sequence rule zn+1 = zn² + c. The text notes that similar fractal structures can be observed in other nonlinear sequences as well.
10. The slider in the Julia set simulation adjusts the gradation of the color shading that indicates the degree of divergence or convergence to zero. By changing the slider, different color schemes are produced, offering additional insight into the convergence landscape and enhancing the visual complexity and beauty of the fractal structures.

Essay Format Questions:

1. Discuss the fundamental relationship between the Mandelbrot set and the Julia sets. How does the Mandelbrot set act as an "index" for the infinite variety of Julia sets?
2. Explain the concept of self-similarity in the context of the Mandelbrot and Julia sets. How does the iterative process contribute to the emergence of these repeating patterns at different scales?
3. Analyze the significance of the boundary of the Mandelbrot set. What distinguishes the points within the set from those outside, and why is this boundary considered a fractal?
4. Consider the role of the complex number c in both the Mandelbrot and Julia set generation. How does the treatment of c (as a variable or a constant) lead to the distinct properties and visual characteristics of these two types of fractals?
5. Based on the information provided, discuss the potential applications or educational value of exploring the Mandelbrot and Julia sets through interactive simulations. What mathematical concepts can these visualizations help to illustrate?

Glossary of Key Terms:

• Complex Number: A number that can be expressed in the form a + bi, where a and b are real numbers, and i is the imaginary unit defined by i² = -1. The a is called the real part, and the b is called the imaginary part.
• Complex Plane: A geometric representation of complex numbers, where the horizontal axis represents the real part and the vertical axis represents the imaginary part. Each complex number a + bi corresponds to a unique point (a, b) in the plane.
• Iteration: A process of repeatedly applying a function or a set of instructions to an initial value. Each application of the function produces a new value, which is then used as the input for the next application.
• Sequence: An ordered list of numbers or other mathematical objects. In the context of fractals, sequences are generated by iterative processes.
• Bounded Sequence: A sequence for which there exists a finite number M such that the absolute value (or magnitude for complex numbers) of every term in the sequence is less than or equal to M. The terms of a bounded sequence do not grow infinitely large.
• Divergent Sequence: A sequence that is not bounded. The terms of a divergent sequence grow indefinitely large in magnitude.
• Magnitude (of a complex number): For a complex number z = a + bi, its magnitude, denoted by |z|, is the distance from the origin (0, 0) to the point (a, b) in the complex plane. It is calculated as |z| = √(a² + b²).
• Fractal: A natural phenomenon or a mathematical set that exhibits a repeating pattern that displays at every scale. It is a shape that looks the same at different levels of magnification. Fractals often have non-integer dimensions.
• Nonlinearity: A property of a system or equation where the output is not directly proportional to the input. The quadratic term (z²) in the Mandelbrot and Julia set formula introduces nonlinearity, which is crucial for the development of complex fractal structures.
• Convergence (to zero): In the context of Julia sets, a sequence zn is said to converge to zero if the terms of the sequence get arbitrarily close to zero as n increases.
• Divergence (to infinity): A sequence zn is said to diverge to infinity if the magnitude of its terms, |zn|, grows without bound as n increases.

Sample Learning Goals

[text]

For Teachers

This is a simulation of a Mandelbrot Set, along with its corresponding Julia Set.

The graph on the left shows the Mandelbrot Set, while the graph on the right shows the corresponding Julia Set of the complex number c, denoted by the white dot on the Mandelbrot Set.

The Mandelbrot Set is a set in the complex plane formed by the recursive equation:

z(1) = z(0)^2 + 1 = 0^2 + (-1) = -1

z(2) = z(1)^2 + 1 = (-1)^2 + (-1) = 0

z(3) = z(2)^2 + 1 = 0^2 + (-1) = -1

z(4) = z(3)^2 + 1 = (-1)^2 + (-1) = 0

z(5) = z(4)^2 + 1 = 0^2 + (-1) = -1

.

.

.

Since the iteration oscillates back and forth between z = 0 and z = -1, the absolute value of z for c = -1 does not tend to infinity. We say that |z| is bounded by a finite value.

Therefore, c = -1 is part of the Mandelbrot Set.

The shape formed by the Mandelbrot Set is also a fractal, where zooming in to the boundary of the shape formed by the set reveals repeating patterns of equal or increasing complexity as the magnification increases.

On the other hand, a Julia Set is formed by fixing the value of c as an arbitrary complex number rather than fixing z = 0. The same recursive equation is run, and the conditions that form the set remain unchanged, but the pattern that emerges changes depending on the value of c that is set.

The degree of divergence or convergence to zero is indicated by colour shading. Its gradation can be changed by a slider, labelled internal convergence, which produces interesting colour schemes.

The colours of the two sets can be changed with the combo box. Available colours are:

- Mixed Colours

- Red

- Green

- Blue

 

Research

[text]

Video

[text]

 Version:

1. http://weelookang.blogspot.sg/2016/02/vector-addition-b-c-model-with.html improved version with joseph chua's inputs
2. http://weelookang.blogspot.sg/2014/10/vector-addition-model.html original simulation by lookang

Other Resources

[text]

Frequently Asked Questions: Mandelbrot and Julia Sets

1. What is the Mandelbrot set and how is it defined?

The Mandelbrot set is a collection of complex numbers, denoted as c, for which the iterative sequence defined by zn+1 = zn2 + c, starting with z0 = 0, does not diverge to infinity. In simpler terms, if you repeatedly apply this formula, and the resulting values of z remain within a finite range (specifically, if the magnitude of z never exceeds 2), then the initial complex number c belongs to the Mandelbrot set.

2. How are points colored in a visualization of the Mandelbrot set?

Points c that are part of the Mandelbrot set are typically colored one way (often black or red in the provided simulation). Points c that are not part of the set (i.e., the sequence diverges) are colored based on how quickly they diverge. The number of iterations it takes for the magnitude of z to exceed 2 is often used to determine the color, with different shades (like green to blue) indicating faster divergence. This coloring scheme reveals the intricate fractal boundary of the Mandelbrot set.

3. What is a Julia set and how does it relate to the Mandelbrot set?

A Julia set is also generated using the same iterative formula: zn+1 = zn2 + c. However, unlike the Mandelbrot set where c varies and the starting value z0 is fixed at 0, for a given Julia set, the value of c is constant, and we examine for which starting points z0 in the complex plane the sequence remains bounded (converges to a finite non-zero value or exhibits bounded oscillation). Each point c in the complex plane has a corresponding unique Julia set.

4. How are Julia sets visualized, and what do the colors represent?

In the visualization of a Julia set (as seen in the right chart of the simulation), points z0 for which the iterative sequence with a fixed c remains bounded are considered part of the Julia set and are often colored a specific way (like the green rim in the simulation for c = 0). Points that diverge are colored based on their rate of divergence, similar to the Mandelbrot set, with color shading indicating the speed of divergence or convergence to zero. A slider in the simulation allows for adjusting the gradation of this shading, creating different visual effects and highlighting the convergence landscape.

5. What happens when you interact with the Mandelbrot set visualization in the provided simulation?

The simulation allows users to draw a rectangle on the Mandelbrot set visualization with the mouse. This action defines a smaller region of the complex plane to be calculated with higher resolution, allowing for closer examination of the fractal details. A "Reset" button returns the view to the initial conditions of the Mandelbrot set. The simulation also features a white dot on the Mandelbrot set that represents the value of c being used to generate the corresponding Julia set displayed in the adjacent chart. This point can be moved with the mouse.

6. How does interacting with the Julia set visualization differ from interacting with the Mandelbrot set visualization?

Similar to the Mandelbrot set, users can draw a rectangle on the Julia set visualization to zoom in on a specific region and increase the resolution. A "Reset" button on the Julia chart returns the view to the Julia set's range for the current magnification level in the Mandelbrot chart. Importantly, a "Reset" on the Mandelbrot chart will revert the Julia set to the one corresponding to c = 0 at the original size of the Mandelbrot set.

7. What causes the fractal nature of the Mandelbrot and Julia sets?

The intricate and self-similar (fractal) structure observed in both the Mandelbrot and Julia sets arises from the fundamental nature of the sequence rule zn+1 = zn2 + c, which is a nonlinear equation. This nonlinearity leads to complex and unpredictable behavior as the iteration progresses, resulting in the infinitely detailed boundaries and repeating patterns characteristic of fractals. The simulation description explicitly mentions that the fractal structure is caused by the nonlinearity of the sequence rule and that similar structures can be observed with other nonlinear sequences.

8. What are some of the learning opportunities or insights provided by the Mandelbrot and Julia set simulation?

The simulation offers a visual and interactive way to understand the concepts of complex numbers, iterative sequences, convergence, and divergence. By exploring the Mandelbrot set and its corresponding Julia sets, users can gain an intuitive appreciation for the relationship between these two mathematical objects. The color shading provides insight into the rate of divergence or convergence, and the ability to zoom in reveals the self-similar nature of fractals. The simulation also highlights how a simple nonlinear rule can generate incredibly complex and beautiful structures, with connections to natural phenomena like coastlines and natural surfaces mentioned in the context of the fine structure of Julia sets for points inside the Mandelbrot set.