About

Snell's law of refractive index

For Teachers

- snelllawrefractionQuantumBoffin.mp4

Credits

Author: tracker file lookang, video QuantumBoffin
Contact: This email address is being protected from spambots. You need JavaScript enabled to view it.

Document Brief: Snell's Law of Refractive Index Using Tracker

This document investigates the behavior of light rays as they pass through the boundary between two media with different refractive indices. Using Tracker, we analyze the angles of incidence and refraction to validate Snell’s Law and calculate the refractive indices of the materials.

Purpose:

To understand the relationship between the angles of incidence and refraction, and to determine the refractive indices of two materials by applying Snell’s Law.

Key Features:

• Analysis of light refraction at the boundary of two media.
• Validation of Snell's Law: n1sin⁡θ1=n2sin⁡θ2​.
• Calculation of refractive indices using experimental data.

Study Guide: Modeling Refraction with Tracker

Learning Objectives:

1. Understand Snell’s Law and its application in determining refractive indices.
2. Measure angles of incidence (θ1​) and refraction (θ2) using Tracker.
3. Validate experimental results with theoretical predictions.

Step-by-Step Guide:

1. Setup and Calibration:

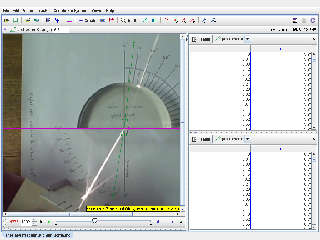
   • Import the video showing the refraction of a light ray at the boundary of two media into Tracker.
   • Calibrate the scale using a known reference, such as a ruler or grid lines visible in the video.

2. Tracking the Light Ray:

   • Identify the point of incidence and draw a normal line perpendicular to the boundary.
   • Track the incoming light ray (incident ray) and the outgoing light ray (refracted ray).

3. Measure Angles:

   • Use Tracker’s protractor tool to measure:
     • The angle of incidence (θ1) between the incident ray and the normal.
     • The angle of refraction (θ2) between the refracted ray and the normal.

4. Apply Snell’s Law:

   • Using the formula: n1sin⁡θ1=n2sin⁡θ2
     • n1​: Refractive index of the initial medium (e.g., air, n1=1).
     • n2: Refractive index of the second medium (to be calculated).
   • Rearrange to calculate n2​:\( n2=n1sin⁡θ1sin⁡θ2n_2 = \frac{n_1 \sin\theta_1}{\sin\theta_2} \)

5. Graphical Analysis:

   • Plot sin⁡θ1​ vs. sin⁡θ2​.
   • The slope of the line gives the ratio n2/n1, which can be used to determine the refractive index.

6. Applications:

   • Validate Snell’s Law for different media combinations.
   • Explore how refractive indices influence the bending of light rays.

Tips for Success:

• Ensure accurate angle measurements by aligning the rays carefully in Tracker.
• Repeat the experiment for multiple angles of incidence to improve accuracy.

FAQ: Snell’s Law of Refractive Index

1. What is Snell’s Law?

Snell’s Law describes the relationship between the angles of incidence and refraction when light passes between two media with different refractive indices:

n1sin⁡θ1=n2sin⁡θ2

2. How do refractive indices affect light refraction?

The refractive index ($n$) determines how much the light ray bends at the boundary. A higher refractive index means the light bends more toward the normal.

3. How is the refractive index calculated in this experiment?

Using Snell’s Law, the refractive index of the second medium (n2) can be calculated as:

n2=n1sin⁡θ1sin⁡θ2

4. What do the graphs of sin⁡θ1\sin\theta_1sinθ1​ vs. sin⁡θ2\sin\theta_2sinθ2​ show?

The graph is a straight line, and the slope of the line represents the ratio n2/n1​. This validates the linear relationship predicted by Snell’s Law.

5. What are the practical applications of Snell’s Law?

• Designing lenses for optical instruments.
• Understanding how light behaves in different media (e.g., water, glass).
• Analyzing total internal reflection in fiber optics.

6. How accurate is this method?

The accuracy depends on precise tracking and measurement of angles. Calibration and repeated measurements can improve reliability.

7. Can Snell’s Law be applied to other waves?

Yes, Snell’s Law applies to any wave, including sound and water waves, traveling between two media with different propagation speeds.